衛星導航高靈敏FFT鎖頻環錯鎖檢測方法
陳 楊,金 天
(北京航空航天大學 電子信息工程學院,北京 100191)
0 引言
商用接收機經常需要工作在城市峽谷、室內等信號條件非常惡劣的環境中,在這些環境下信噪比往往很低,傳統接收機無法勝任[1]。為了滿足在弱信號條件下的導航定位需求,人們對高靈敏衛星導航接收機進行了深入的研究,而高靈敏跟蹤環路的設計是整個高靈敏接收機中非常關鍵的一環。在常見的高靈敏鎖頻環路中,高靈敏快速傅里葉變換(fast Fourier transformation,FFT)鎖頻環因為其良好的性能,受到了廣泛的關注;但目前的研究內容大多集中在如何進一步提升FFT環路的靈敏度[2-3]以及動態性[4]上,對于高靈敏FFT環路錯鎖的成因以及檢測問題,相關的研究還比較少。
在傳統環路中,錯鎖的產生是因為頻率誤差超出了線性鑒頻范圍,當相干積分時間為Tcoh,且鑒頻器的鑒頻范圍為±1/2Tcoh時,最終跟蹤環路將錯鎖于1/Tcoh[5]。針對傳統環路,文獻[6]分析了錯鎖發生時鎖頻環和鎖相環的狀態,發現當錯鎖發生時I支路積分值會發生翻轉,據此提出了一種利用I支路積分值翻轉計數來進行錯鎖檢測的方法,并利用仿真數據對方法進行了驗證。文獻[7]從最優化數字濾波器設計和鎖頻鎖相環融合的角度,提出了一種新型的相位鎖定環路(phase lock loop,PLL),稱為模糊頻率輔助PLL。從仿真和實測結果來看,該環路可以有效抑制錯鎖情況的發生,并具有良好的動態性。文獻[8]對傳統的叉積鑒頻方法進行了改進,將鑒頻對象從2個相鄰偽碼周期信號變成1個偽碼周期信號的相鄰半個周期,由此提出了一種利用相關能量的高低來進行誤鎖檢測的方法。但高靈敏FFT跟蹤環路的鎖頻原理與傳統環路不同,其錯鎖點成因以及錯鎖位置與傳統環路有顯著差別,上述方法并不能直接適用。
本文通過分析高靈敏FFT鎖頻環錯鎖原因,提出一種錯鎖檢測方法,從檢測概率和虛警率2個角度分析方法的理論性能并加以驗證。
1 FFT鎖頻環原理
傳統的數字鎖頻環是由模擬環路通過線性z域變換等方式得到的,變換過程本身就會導致實際環路噪聲帶寬大于理論帶寬值,當環路預檢積分時間變長時,經典數字環路參數均不再理想,將導致環路穩定性變差[9]。
不同于傳統環路,基于FFT的高靈敏載波跟蹤算法使用FFT頻域分析方法同時輔以導航電文估計技術來替代鑒別器功能:FFT頻域分析方法具有較寬的誤差提取線性范圍,從而有效地避免了環路非線性失真[2];舍棄了環路濾波器,根據有無信號時FFT環路輸出的序列特點來設置后驗估計門限,當FFT輸出峰值超出該門限時,表明算法得到了當前的頻差估計。FFT鎖頻環的工作原理如圖1所示。
假設輸入信號ui(t)的偽碼已經被剝離,可表示為
(1)
式中:a為幅度;D(t)為調制在載波上的數據碼;fi和θi分別為輸入頻率和輸入初相位。壓控振蕩器產生了正弦和余弦2路載波信號,分別與輸入信號相乘,對應地可以表示為
(2)
式中f0和Q0分別為本地復制信號的頻率和初相位。輸入信號與正余弦弦載波復制信號相乘后分別得到同相和正交信號,通過Tcoh長度的預檢測積分,這里假設積分時間內沒有電文跳變,并且積分時間足夠長,足以將高頻成分濾除,得到I(n)和Q(n)為
(3)

(4)
則二者相加后復數相量
R(n)=I(n)+jQ(n)=aD(n)sinc (feTcoh)ej(2πfenTcoh+θe)。
(5)
式中j代表虛部。因為不同積分值中間可能會有電文跳變,送入FFT運算之前,需要對導航電文進行估計,消除符號后才能進行FFT運算。可得消除符號后的復向量為
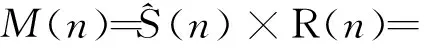
(6)
S(n)=sign(D(n)D(n-1))。
(7)
式中sign為符號函數。假設fe在期間沒有發生變化,則
(8)
式中:I(n)、Q(n)、I(n-1)、Q(n-1)為由式(3)得到的第n和第n-1個積分值;Δφ為前后2個周期的相位差,即
Δφ=2πfeTcoh。
(9)
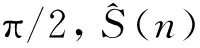
(10)
文獻[2]指出有信號和無信號時,|F(k)|分別滿足萊斯分布和瑞利分布,并給出了給定虛警率pF下的判決門限
(11)
(12)
2 高靈敏FFT環路錯鎖原因分析
對于高靈敏FFT環來說,假設做N點FFT,當頻差為fe時,由前面的分析可知最終輸出的fout受到頻差fe、鑒頻模糊誤差fe,v和電文翻轉值判斷錯誤誤差fe,s3者共同影響,可得
fout=fe+fe,s+fe,v。
(13)
對于傳統環路來說,其輸出僅僅受頻差fe和鑒頻模糊誤差fe,v影響,這種差異也最終導致了二者錯鎖點的成因和位置的不同。
式(9)反映了fe與相位角Δφ之間的關系,將式(9)代入式(8)中有
(14)
結合式(7)和式(14)有
(15)
(16)
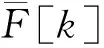
(17)
式中:當|fe|=1/2Tcoh時,fe,v可能為±1/Tcoh或0。根據不同fe條件下的fe,s和fe,v的取值,由式(13)可得
(18)
由式(18)可以看出:當|fe|=1/2Tcoh和|fe|=1/Tcoh時,鑒頻器輸出為0。對存在的頻率誤差無法鑒出,從而產生錯鎖現象。
與相干積分時間同樣是Tcoh的傳統環路相比,FFT鎖頻環存在2種可能的錯鎖類型:1/Tcoh類型錯鎖位置與傳統環路相同,錯鎖原因也與傳統環路相似;1/2Tcoh類型是FFT環獨有的,這個特有的錯鎖類型并不是一個穩定的錯鎖類型,與高靈敏環路對電文的估計準確度有關。
3 高靈敏FFT環路錯鎖檢測
高靈敏FFT環路擁有2種錯鎖類型,其中1/Tcoh錯鎖類型的檢測方法可以參考文獻[6],而對于1/2Tcoh錯鎖類型,傳統的檢測方法在沒有PLL輔助的情況下就無法正常工作,所以下面著重討論1/2Tcoh錯鎖類型的檢測。
在已經位同步的前提下,可以得到處于同一個電文符號下的M(n)。假設電文周期為TD,相干積分時間為Tcoh,FFT點數為N,那么一個電文周期下將會有l個積分值(l=TD/Tcoh)。當|fe|=1/2Tcoh時,M(n)的符號在一個電文周期下將會交替翻轉,整個檢測周期內總共將發生Cre次翻轉,即
(19)
考慮有噪聲的情況,假設誤碼概率為Pe,設置門限值d,即翻轉次數大于d次即認為錯鎖,則其檢測概率pD和虛警率pF分別為
(20)
以全球定位系統(global positioning system,GPS)L1信號為例,其電文周期TD為20 ms。當Tcoh為10 ms、FFT點數為100時,由文獻[11]可以計算出不同的載噪比條件下的Pe。從式(20)得pD和pF,對應的特性曲線如圖2和圖3所示。
對比2圖可以看出,在弱信號條件下,當20 為了驗證錯鎖檢測算法的效果,利用GPS采集器于2017-01采集了一組時長150 s的跑車數據,其采樣率為62 MHz,中頻為4.17 MHz。測試條件:使用相干積分時間為10 ms、100點的FFT鎖頻環,測試地點位于中關村附近(如圖4所示),測試的跑車軌跡如圖5所示。這個路段高樓密集,信號環境比較惡劣,容易發生錯鎖。算法判決門限d設置為25。 GPSL1 12號衛星無錯鎖檢測和有錯鎖檢測的多普勒變化及載噪比情況見圖6、圖7。 由圖6可以看出,無錯鎖檢測所對應的多普勒曲線逐漸偏離有錯鎖檢測環路的多普勒曲線,因為FFT鎖頻環的相干積分時間是10 ms,點數是100,所以整個環路的更新周期是1 s,整個多普勒曲線呈階梯狀下降,最終與有錯鎖檢測的高靈敏FFT環路的輸出值相差接近50 Hz,保持這個差值不變,穩定在了1/2Tcoh錯鎖類型。從圖7可以看出與有錯鎖檢測的環路相比,無錯鎖檢測的環路載噪比平均低了3 dBHz左右,這是因為跟蹤的載波頻率與真實值相差了50 Hz。同時從圖中可以看出在錯鎖發生后的2 s內,檢測算法完成了錯鎖的檢測工作,跟蹤環路重新正確跟蹤上了導航信號。 本文通過對高靈敏FFT鎖頻環的原理和錯鎖成因的分析,確定了FFT鑒頻結果由真實的頻差、鑒頻模糊和導航電文剝離錯誤這3個方面的因素共同決定。考慮到上述因素的鑒頻取值范圍,發現了高靈敏FFT鎖頻除了具有和傳統環路相同的1/Tcoh錯鎖類型,還具有1/2Tcoh錯鎖類型。根據1/2Tcoh錯鎖類型發生時積分值的翻轉規律,提出了相應的錯鎖檢測方法,分析了該方法在不同門限和載噪比下的虛警率和檢測概率,并給出了弱信號條件下的建議門限設置方法。通過對實際衛星導航數據的測試,驗證了上述方法的可行性。測試結果表明該算法可以在幾十個電文周期內對錯鎖進行檢測,進而降低錯鎖對環路跟蹤的影響,對高靈敏度衛星導航接收機研制具有一定意義。后續可進一步開展跟蹤環路錯鎖重新跟蹤方法的研究,進一步簡化錯鎖檢測過程。 [1] SIDDAKATTE R K,BROUMANDAN A,LACHAPELLE G.Use of diversity techniques for weak GNSS signal tracking in fading environments[C]//The Institute of Electrical and Electronic Engineers(IEEE).Ubiquitous Positioning Indoor Navigation and Location Based Service(UPINLBS).New York:IEEE,2014:1-10. [2] 王勇松.高靈敏度GNSS關鍵接收技術研究[D].杭州:浙江大學,2010. [3] YAN K,ZIEDAN N I,ZHANG H,et al.Weak GPS signal tracking using FFT discriminator in open loop receiver[J].GPS Solutions,2016,20(2):225-237. [4] WANG X,JI X,FENG S,et al.A high-sensitivity GPS receiver carrier-tracking loop design for high-dynamic applications[J].GPS Solutions,2015,19(2):225-236. [5] 謝剛.GPS原理與接收機設計[M].北京:電子工業出版社,2009. [6] 李國棟,崔曉偉,尹旭明,等.GPS接收機中鎖頻環頻率誤鎖的檢測[J].清華大學學報(自然科學版),2007,47(1):69-72. [7] RONCAGLIOLO P A,GARCA J G,MURAVCHIK C H.Optimized carrier tracking loop design for real-time high-dynamics GNSS receivers[J].International Jouranl of Navigation and Observation,2012,2012(4):1-18. [8] 鄭晶,王祖林,趙毅寰.擴頻接收機中改進的鎖頻方案[J].電子對抗,2010(3):39-44. [9] KAZEMI P L.Optimum digital filters for GNSS tracking loops[C]//The Institute of Navigation.Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008).Savannah:IEEE, 2008:2304-2313. [10] 奧本海姆 A V,謝弗 R W,巴克 J R,等.離散時間信號處理[M].劉樹棠,黃建國,譯.西安:西安交通大學出版社,2001:437-442. [11] 何忠蛟.數字通信系統中信噪比與誤碼率關系的Matlab模擬[J].湖北民族學院學報(自科版),2006,24(1):37-38.4 實驗與結果分析
5 結束語

