利用真人實驗教授經濟學基本原理

馮霞+高翔

[摘 要]為了全面培養通識教育下的創新型人才，面向理工科學生在內的各個專業的學生教授經濟學、金融學基礎知識的課程越來越多。但是在傳統教學方法下，抽象概念的講解，不僅不利于學生的理解，也難以激發其學習的興趣。本文提出了一種通過借鑒少數者博弈模型的思路而設置的真人實驗，通過寓教于樂的方式讓學生理解、體會抽象的經濟學、金融學基本原理。

[關鍵詞]真人實驗；經濟學原理；少數者博弈模型

[中圖分類號] G64 [文獻標識碼] A [文章編號] 2095-3437（2018）01-0132-03

為了滿足通識教育下的創新型人才培養[1]的需要，大學教育中越來越多地引入了面向各專業，特別是理工科學生[2][3]的社科類基礎課程，比如經濟學概論。但是抽象的經濟學基本原理經常讓學生難以理解，并且傳統的課堂教學中所選案例也多是宏觀的經濟現象，不貼近學生的生活體驗，所以難以激發學生的學習興趣。[4]對于在專業學習中已培養出實證精神的理工科學生而言，難懂和無趣很容易誘發出其厭學甚至是質疑的態度。

本文首倡一種新的教學方式，即從追求實證的科學批判思維出發[5]，利用簡便可控的真人實驗，讓學生參與其中，以便其理解經濟學中抽象的基本原理，比如“看不見的手”等重要概念。該真人實驗，參照少數者博弈模型的基本思路而設置，既能幫助學生在充滿參與感的情境下激發學習熱情，也能啟發學生從簡單的博弈游戲出發深入思考其中蘊藏的經濟學原理。[6]

一、經濟學基本原理之一“看不見的手”與少數者博弈模型

經濟學中最重要的基本原理，即是市場經濟中發揮基礎調節作用的所謂“看不見的手”。這是一個隱喻，最早由英國經濟學家亞當·斯密提出：“每個人都試圖應用他的資本，來使其生產品得到最大的價值。”對此，我們可以理解為市場上每個投資人都希望將持有的資金投入高回報的行業中去，從而產生高于市場全行業平均利潤率的回報。但是如果投資到某過剩行業，很容易造成產能過剩，供大于求，進而引起利潤率的下降；而相反的，如果投資供不應求的新興行業，回報率將會顯著高于市場的整體回報率。

對于這一基本原理的微觀解釋，一直是科研人員關心的重要問題。[7，8]最新的研究表明，我們可以借助于少數者博弈模型來幫助解決這個難題。[9]該模型的常見表述為：“生活在社會群體中的人們常常會遇到這樣的問題，比如有許多決策人同時面臨兩種選擇時，如果決策人的選擇是較少人的選擇，就將獲益，否則將會失利。”類比到上文我們已經講到的關于行業選擇的經濟問題，可以看出，未達到過剩投資的行業，其利潤率就會比較高，其行業投資人就會比過剩行業的投資人獲得更高的回報。而高回報的行業就會吸引更多的投資，進而誘發該行業滑向產能過剩，利潤率下降的窘境。相反對于低回報的行業，隨著投資人的離去，去產能后利潤率則會好轉。總的來講，少數者博弈模型可以對應為投資人在高回報與低回報的行業間不停地轉換，追逐最大利潤的博弈游戲。

二、實驗設置和過程

基于上面的分析，我們可以借鑒少數者博弈模型的基本思路，來設置簡單的博弈游戲，并將其引入課堂教學中，寓教于樂，讓學生在扮演投資人角色的過程中，深切的體會自己被“看不見的手”推動著追求最大利潤的過程。

具體的設置如下：

1.首先統計課堂上學生的總人數，記為N。

2.設置兩個可供選擇行業，學生可以通過舉手或是不舉手來表示自己選擇進入行業1還是行業2。

3.統計選擇行業1的學生人數，也就是舉手的學生人數，記為N1。

4.如果N1小于N-N1，則本輪選擇進入行業1的學生（即舉手的學生）勝利，可以給自己加2分；同時，選擇進入行業2的學生（即不舉手的學生）失敗，給自己減1分。（起始分都是0分）。

5.博弈游戲一共進行若干回合（回合數視課堂時間而定，但是為了消除誤差，提高實驗結果的有效性，最好大于5）。

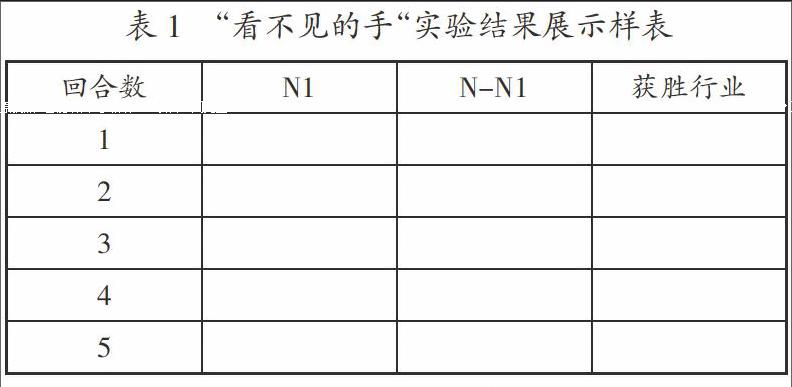
6. 每一回合，都應把統計到的N1和N-N1的值，以及獲勝的行業填入表1展示給學生，以便幫助學生在下一回合做出自認為正確的選擇。

7. 博弈游戲的最后，統計所有學生的得分情況。為了激發學生投入博弈游戲的熱情和認真參與實驗的態度，建議給予得分最高的若干學生一定的獎勵，比如給其平時成績加分。

三、結合實驗結果教授經濟學基本原理

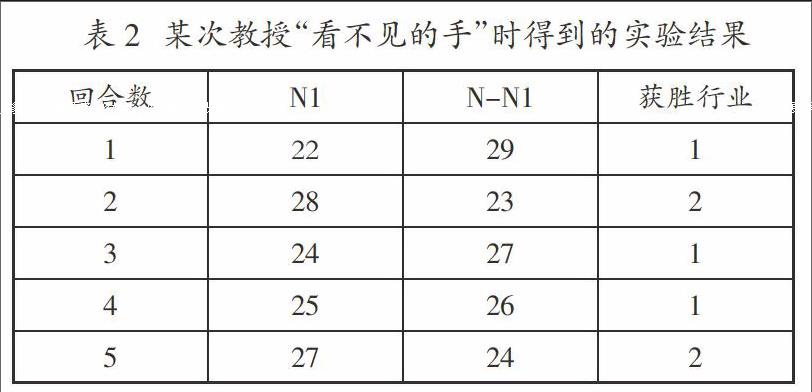
我們將通過某次授課時得到的實驗結果（見表2）來講解該博弈游戲體現出的經濟學原理和啟發。

本次實驗參與的學生人數為N=51，一共進行了5回合的博弈游戲。開始前，已向學生講明了博弈游戲的規則和獲勝者將獲得獎勵的事項。在博弈游戲結束后，我們可以根據表2的結果做出以下分析和講解：

1.每個學生對結果的影響都是相同的，即一人一票，沒有任何學生擁有比其他人更高的權重。同時，博弈游戲的歷史信息及時全面的展現在所有學生面前，沒有任何隱瞞。另外，任何一個學生都是在無法獲知其他所有學生的選擇下，獨立自主的做出選擇的。以上三條就構成了博弈游戲中公平競爭的環境。

2.在公平競爭的環境下，每個回合兩個行業的人數基本相同。特別是在經歷了初始2個回合的過渡后，兩邊的人數保持在了一個穩定比例（1：1）。同時兩個行業獲勝的次數也基本相近（2：3）。這意味著，公平競爭下沒有哪個行業是永遠的暴利行業；參與競爭的每個人在追求自身獲利最大（博弈游戲中得分最高）的驅動下，自然而然地實現了市場均衡。

3.在最后統計所有學生得分的情況時，我們發現學生的得分基本符合正態分布。這意味著在公平競爭的情況下，沒有任何策略可以保證穩贏的結果，即沒有套利機會的出現，因此每個人每回合的獲勝與否就是隨機的結果。

以上便是利用少數者博弈模型的實證思路設置的博弈游戲及其實際教學情境。從中我們可以發現，關于“看不見的手”這個抽象的經濟學原理中包含的教學難點和重點，比如信息透明，公平競爭，市場均衡，無套利等，都已寓教于樂。學生不但參與度高，而且情境式教學也有助于對抽象概念進行理解和掌握。endprint

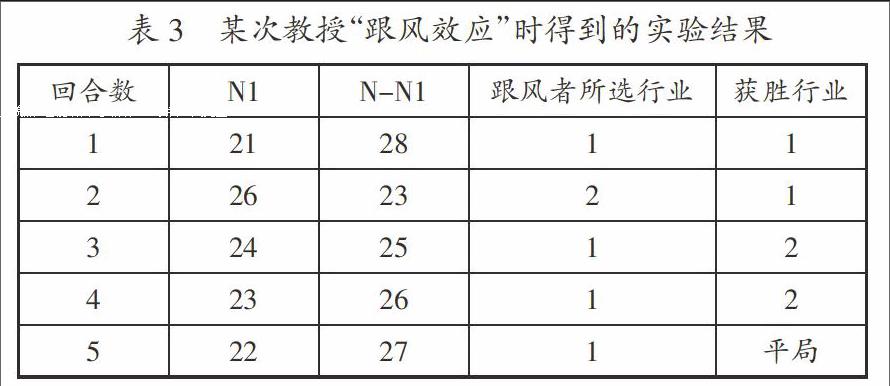
四、利用真人實驗教授“跟風效應“

同時，利用相同的實證思路，通過改變游戲規則，也可以教授“跟風效應”這一重要經濟學、金融學知識。“跟風效應”，也可稱為“羊群效應”或是“從眾效應”，是指由于群體的影響或壓力，而使得個人的觀念或行為非理性地趨向于多數人相一致的方向。這類現象在日常的經濟生活中，既體現在人們容易盲從于時尚、口碑或是朋友推薦下的非理性購買行為，也對應于房地產等行業中常見的“買漲不買跌”的現象。在金融市場上，“跟風效應”對應于在股票市場的泡沫期，一些投資分析能力有限的散戶，在夸大的高收益宣傳下未經理性思考就涌入股票市場，甚至盲從于所謂投資大師的推薦而高杠桿重倉持有某只股票，卻并未清楚地認識到自己將面臨的巨大風險。這些現象反映了“跟風效應”的本質，即本應具有自主判斷能力的個體，在群體的壓力下部分或完全地喪失了自我判斷能力，而盲從于群體或是某個具有影響力的個體。

為了通過相似的博弈游戲，讓學生理解“跟風效應”的本質及其結果，我們可以設置以下游戲規則：

1.首先統計課堂上學生的總人數，記為N。

2.設置兩個可供選擇行業，學生可以通過舉手或是不舉手來表示自己選擇進入行業1還是行業2。

3.統計選擇行業1的學生人數，也就是舉手的學生人數，記為N1。選擇行業2的學生人數，也就是不舉手的人數，記為N-N1。

4.設置跟風者的數目為F=N×10%（取整）。

5.如果N1

6.如果在跟風者跟隨進入行業1的情況下（N1

a）如果N1N-N1，則本輪選擇進入行業1的學生（即舉手的學生）失敗。

b）如果N1+F=N-N1，則視為平局，雙方學生均加1分。

7.博弈游戲一共進行若干回合（回合數視課堂時間而定，但是為了消除誤差，提高實驗結果的有效性，最好大于5）。

8.每一回合，都應把統計到的N1和N-N1的值，跟風者的選擇，以及獲勝的行業展示給學生，以便幫助學生在下一回合做出自認正確的選擇。

9.博弈游戲的最后，統計所有學生的得分情況。為了激發學生投入博弈游戲的熱情和認真參與實驗的態度，建議給予得分最高的若干學生一定的獎勵，比如給其平時成績加分。

可以看到，模擬跟風效應的博弈游戲規則相比之前的規則，只是增加了少量的跟風者（規則4）及其選擇行業的機制（規則5），并相應改變了勝利條件（規則6）。但參照表3我們可以預見到，在選擇兩個行業的人數本身就差別不大的情況下，少量跟風者的引入（N×10%），將顯著地改變每回合的結果，從而迫使具有自主選擇能力的參與者（學生）重新制訂自己的策略，進而做出不同的選擇。表3給出的某次授課時得到的實驗結果中，學生參與總人數N=49，因此設置跟風者的數量為F=N×10%≈5。

綜上，我們可以看到一種新的教學方式的雛形，即借鑒少數者博弈模型的思路設置真人實驗，通過寓教于樂的方式讓學生理解、體會包括“看不見的手”、“跟風效應”等抽象的經濟學、金融學基本原理。

[ 參 考 文 獻 ]

[1] 孔德懿，魏丹.通識教育視野下的創新人才培養[J].大學教育，2015（3）：66-68.

[2] 葛欣.基于大理科模式的拔尖學生培養的探索與實踐[J].大學教育，2016（3）：46-47.

[3] 林小英，翁仁貴，劉志鵬.德國大學教育對我國“卓越計劃”的啟示[J].大學教育，2016（2）：15-16.

[4] 張吉軍，賈昕宇，王宏立，楊忠國，劉天祥，戶春影，代洪慶，李寶玉.淺論應用型普通高校課堂教學模式變革的必要性——基于高等教育改革發展的視角[J].大學教育，2016（3）：17-19.

[5] 趙詩華，陳熹，馮玉.淺談創新訓練與批判性科學思維的培養——國家精品課程推薦與相關思考[J].大學物理，2015（12）：37-39.

[6] 劉呂紅，肖孟夏.啟發、自主、合作、探究、反饋——“探究式-小班化”課堂教學模式的理論研究[J].大學教育，2016（4）：1-3.

[7] 劉建華，杜明義，呂書強，趙江洪，龐蕾.科研項目式教學方法與創新能力培養模式研究[J].大學教育，2016（4）：29-30.

[8] 肖井華， 楊胡江， 李海紅. 探索課程教學與科學研究的融合，促進教研相長[J].大學物理， 2014（6）：33-40.

[9] 黃吉平.經濟物理學：用物理學的方法或思想探討一些經濟或金融問題[M].北京：高等教育出版社，2013.

[責任編輯：鐘 嵐]