基于ANSYS二次開發(fā)的高階連續(xù)梁數(shù)值模擬★

殷玉沉 朱彥濤 孫玉周

(1.中原工學(xué)院，河南 鄭州 450007； 2.西藏職業(yè)技術(shù)學(xué)院，西藏 拉薩 850000)

0 引言

高階連續(xù)理論能夠反映出特殊本構(gòu)反應(yīng)，例如在偶應(yīng)力理論、應(yīng)變梯度連續(xù)理論中引入尺度因子描述高階連續(xù)結(jié)構(gòu)的局部彎曲效應(yīng)[1-3]。在研究高階連續(xù)結(jié)構(gòu)過程中，尺寸效應(yīng)的影響日益被重視，但是傳統(tǒng)有限元法構(gòu)造高階形函數(shù)需要大量的工作[4]，而且沒有引入尺度因子不易實(shí)現(xiàn)數(shù)值模擬。采用傳統(tǒng)有限元法分析計(jì)算，會(huì)遇到網(wǎng)格劃分困難以及近似函數(shù)不連續(xù)等問題，但應(yīng)用適當(dāng)?shù)幕瘮?shù)和權(quán)函數(shù)，移動(dòng)最小二乘法(MLS)可以比較容易地構(gòu)造出高階形函數(shù)[5,6]。近年來，一些學(xué)者對(duì)相關(guān)問題進(jìn)行了研究，李雷等[7]將無網(wǎng)格法和高階理論相結(jié)合，對(duì)巖土工程中的一些問題進(jìn)行數(shù)值模擬；李莉等[8]利用虛功原理建立各向異性修正偶應(yīng)力理論并引入不同的材料細(xì)觀參數(shù),建立適用于層合板/夾層板的偶應(yīng)力理論模型；孫玉周等[9，10]使用無網(wǎng)格法研究基于高階連續(xù)理論下的碳納米管的多尺度效應(yīng)以及彎曲梁等問題。上述的研究主要集中在通過無網(wǎng)格法與高階理論相結(jié)合，以及考慮結(jié)構(gòu)尺度效應(yīng)影響等方面，但是將高階連續(xù)理論應(yīng)用在有限元分析中以及將其在有限元軟件中實(shí)現(xiàn)數(shù)值模擬的研究較少。

ANSYS作為有限元領(lǐng)域的大型通用軟件，被世界各工業(yè)領(lǐng)域廣泛接受。為適應(yīng)具體工程需求，ANSYS還提供了APDL,UPFs,UIDL(用戶界面設(shè)計(jì)語言)及TckTk(工具命令語言/圖形開發(fā)工具箱)4種二次開發(fā)工具[11]。針對(duì)本文提出的問題，由于ANSYS在網(wǎng)格劃分以及高階連續(xù)結(jié)構(gòu)分析上存在局限性，需要對(duì)ANSYS軟件進(jìn)行二次開發(fā)。本文采用移動(dòng)最小二乘法可以方便的構(gòu)造高階連續(xù)形函數(shù)的優(yōu)點(diǎn)，建立高階連續(xù)梁模型，通過Fortran語言編寫用戶單元子程序，進(jìn)行ANSYS的二次開發(fā)，實(shí)現(xiàn)高階連續(xù)梁在有限元軟件中的數(shù)值模擬，并引入尺寸因子對(duì)高階連續(xù)梁進(jìn)行分析。

1 基于MLS的計(jì)算框架

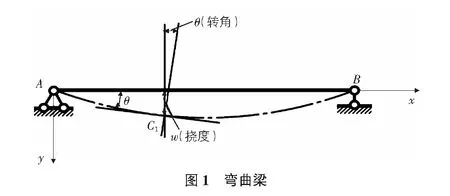
在傳統(tǒng)彎曲梁(如圖1所示)的基礎(chǔ)上，高階連續(xù)梁模型的應(yīng)力和應(yīng)變分別定義為：

應(yīng)變：

(1)

應(yīng)力：

σxx=Eεxx+lxεxxx
τxxx=g2Eεxxx+lxEεxx
τyxx=g2Eεyxx

(2)

其中,E為彈性模量；w為梁的撓度；g為體本征尺度因子；lx為面本征尺度因子。

梁在應(yīng)變能及外力的作用下，根據(jù)虛功原理可得:

(3)

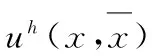
(4)

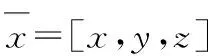
令m=4,則一維三次基函數(shù)為:

aT(x)=(1,x,x2,x3)

(5)

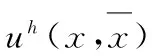
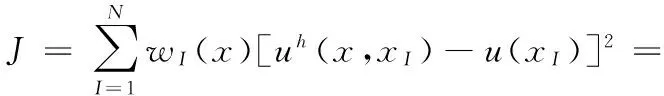
(6)

其中，wI(x)=wI(x-xI)為節(jié)點(diǎn)xI處的權(quán)函數(shù)，當(dāng)權(quán)函數(shù)wI(x)在節(jié)點(diǎn)支撐域范圍內(nèi)時(shí)，wI(x)>0，否則，wI(x)=0。

由式(3)得：

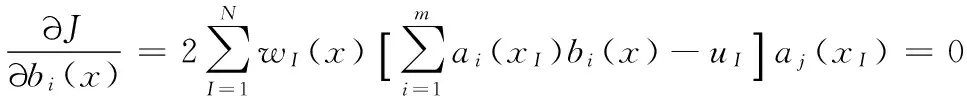
j=1,2,3,…，m

(7)

由此得:

(8)

即:

A(x)b(x)=B(x)u

(9)

令：

B(x)=[wI(x)a(xI)w2(x)a(x2)…wN(x)a(xN)]

(10)

則形函數(shù)為：

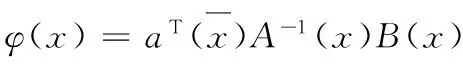
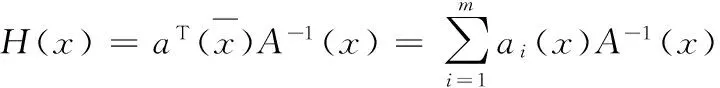
(11)

權(quán)函數(shù)ωI(x)在節(jié)點(diǎn)xI處的值最大，而且支撐域邊界附近趨于0，即當(dāng)r=(x-xi)/dmI>1時(shí)，w(r)=0，dmI為節(jié)點(diǎn)支撐域的直徑。

采用三次樣條權(quán)函數(shù)，綜上可求得形函數(shù)φ(x)的導(dǎo)數(shù)為:

φI,x(x)=H,x(x)B(x)+H(x)B,x(x)l
φI,xx(x)=[H,xx(x)B(x)+2H,x(x)B,x(x)+H(x)B,xx(x)]l
φI,xxx(x)=[H,xxx(x)B(x)+3H,x(x)B,xx(x)+3H(x),xxB,x(x)+H(x)B,xxx(x)]l

(12)

在無網(wǎng)格法的計(jì)算框架下，撓度的二階和三階導(dǎo)數(shù)近似為:

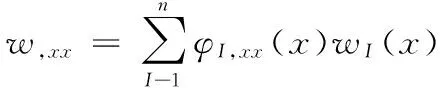
(13)

由式(12),式(13)代入式(3)可得高階連續(xù)梁的總剛度矩陣表達(dá)式：

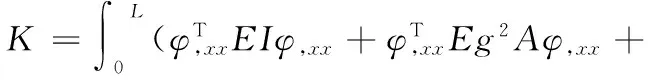
(14)

由式(14)可知，高階連續(xù)問題中出現(xiàn)高階位移導(dǎo)數(shù)，傳統(tǒng)有限元法處理高階形函數(shù)的工作量比較大，利用移動(dòng)最小二乘近似(MLS)構(gòu)造高階形函數(shù)，位移高階導(dǎo)數(shù)可以直接通過節(jié)點(diǎn)位移插值得到。

2 ANSYS二次開發(fā)

基于ANSYS為用戶提供的二次開發(fā)功能，通過UPFs的特性實(shí)現(xiàn)ANSYS軟件模擬一維高階連續(xù)梁。由于ANSYS中傳統(tǒng)彎曲梁缺少高階連續(xù)理論，下面將含有的高階項(xiàng)從高階連續(xù)梁中分離出來即K1。通過添加附加項(xiàng)K1到用戶自定義程序UELMatx.F中，實(shí)現(xiàn)高階連續(xù)理論在有限元軟件中的應(yīng)用。

從式(14)得：

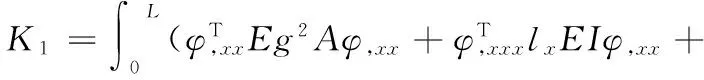
(15)

ANSYS的用戶子程序UELMatx用于訪問單元矩陣和載荷向量，主要目的是修改或監(jiān)視單元?jiǎng)偠染仃嚭秃奢d向量。程序編譯過程中需要解決的關(guān)鍵問題主要在以下方面：

1)ANSYS二次開發(fā)編譯鏈接環(huán)境建立；

2)利用APDL(參數(shù)化設(shè)計(jì)語言)創(chuàng)建節(jié)點(diǎn)支撐域覆蓋范圍內(nèi)的單元；

3)將附加項(xiàng)K1通過編譯用戶自定義程序UELMatx實(shí)現(xiàn)與有限元軟件結(jié)合。

ANSYS源程序是基于FORTRAN語言編寫，為方便程序編譯鏈接，采用FORTRAN語言對(duì)程序進(jìn)行編譯開發(fā)。本文基于ANSYS15.0進(jìn)行二次開發(fā)，程序編譯鏈接過程如下:

1)將編譯完成的子程序UELMatx.F放置在ANSYS Incv150ansyscustomuserwinx64文件夾中，使用該文件夾下的ANSCUST.BAT批處理文件，編譯連接成功后生成用戶自定義ANSYS.exe文件；

2)激活UPFs：打開ANSYS15.0>Mechanical APDL Product Launcher 15.0，選擇用戶自定義生成的ANSYS.exe文件路徑，也可通過GUI操作進(jìn)行。該用戶子程序在求解之前調(diào)用，調(diào)用命令如下：USRCAL,UELMATX。

3 算例分析

3.1 簡(jiǎn)支梁的計(jì)算分析

如圖1所示，利用簡(jiǎn)支梁的例子來驗(yàn)證編譯開發(fā)的用戶子程序UELMatx在ANSYS中調(diào)用求解時(shí)的收斂性及精確度。簡(jiǎn)支梁受集中力F=1 N作用在跨中，梁的長(zhǎng)度為10 mm，梁截面高度h=1 mm，厚度b=0.01 mm，梁的橫截面面積A=h×b，彈性模量E=1.0×105MPa。

本文利用Beam3單元建立一維梁模型，為驗(yàn)證高階連續(xù)梁在ANSYS二次開發(fā)后的數(shù)值計(jì)算精度，與基于無網(wǎng)格法的一維高階連續(xù)梁的數(shù)值計(jì)算結(jié)果進(jìn)行對(duì)比。梁上布置不同的節(jié)點(diǎn)數(shù)，梁中點(diǎn)撓度變化見表1。

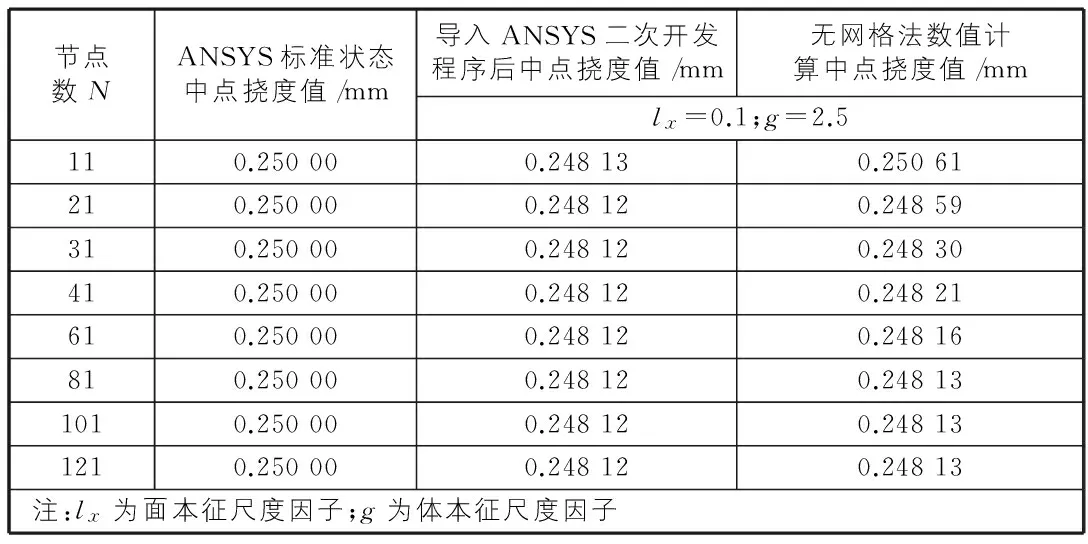
表1 不同節(jié)點(diǎn)數(shù)時(shí)梁中點(diǎn)撓度值

假設(shè)一維簡(jiǎn)支梁的面本征尺度和體本征尺度為固定值。由表1的計(jì)算結(jié)果可以看出，不同節(jié)點(diǎn)數(shù)的一維高階連續(xù)簡(jiǎn)支梁通過ANSYS二次開發(fā)模塊求解的中點(diǎn)撓度值收斂且基本與無網(wǎng)格法框架下的數(shù)值計(jì)算結(jié)果吻合。

從表1的數(shù)據(jù)可以知道高階連續(xù)理論下的簡(jiǎn)支梁中點(diǎn)撓度值與ANSYS標(biāo)準(zhǔn)狀態(tài)下的結(jié)果存在極小差異。利用ANSYS二次開發(fā)后的計(jì)算模塊分析尺度因子的變化對(duì)梁的撓度影響，相關(guān)實(shí)常數(shù)不變，只改變尺寸因子的數(shù)值，計(jì)算結(jié)果分別見表2,表3。

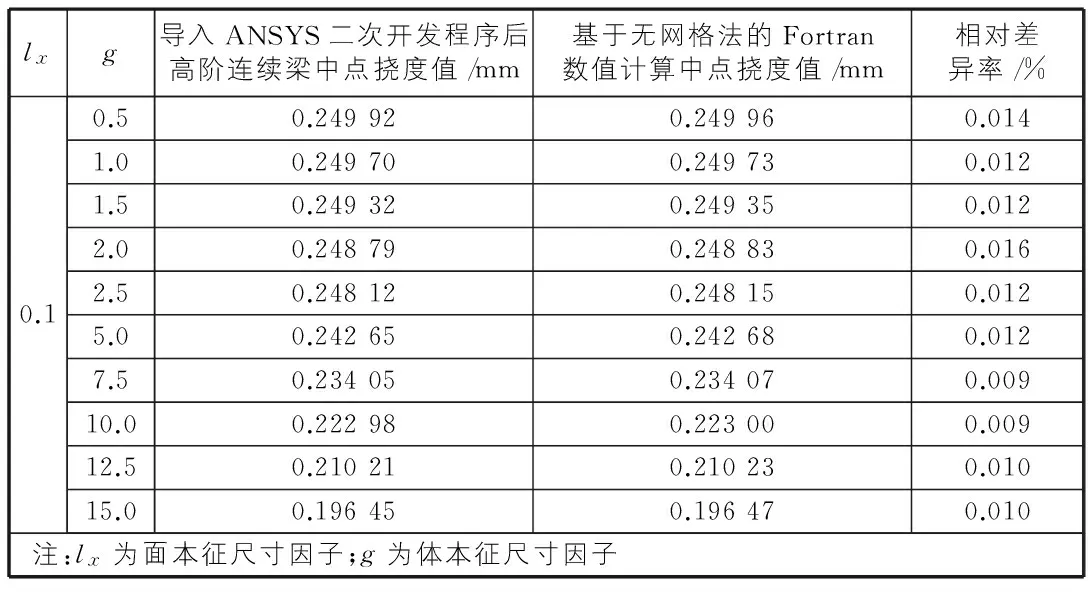
表2 尺寸因子g變化時(shí)對(duì)高階連續(xù)梁中點(diǎn)撓度值

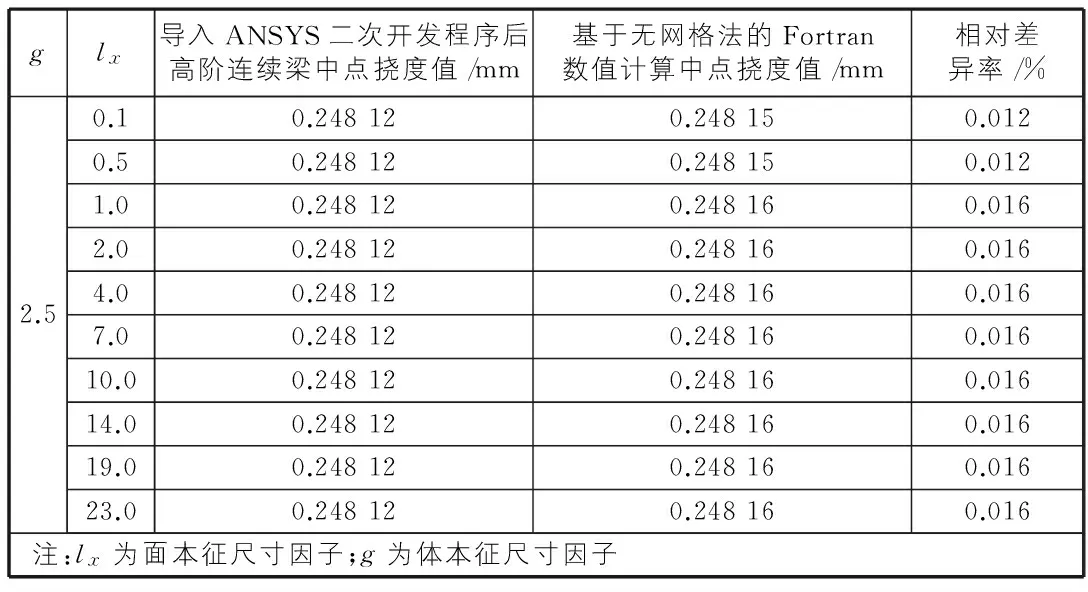
表3 尺寸因子lx變化時(shí)對(duì)高階連續(xù)梁中點(diǎn)撓度值

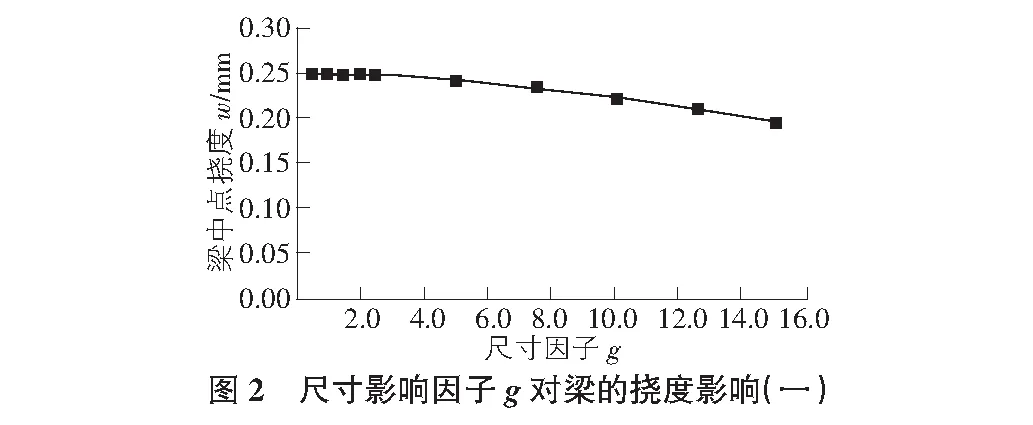
由表2,表3可知，當(dāng)尺寸因子g為定值，面本征尺寸因子lx從0.1變化到23，隨著lx值的逐漸增大，對(duì)高階連續(xù)梁的撓度值影響極小；當(dāng)面本征尺寸因子lx不變，g從0.5變化到15.0，對(duì)梁的撓度變化有較大影響，其影響趨勢(shì)如圖2所示。

3.2 懸臂梁的計(jì)算分析

通過導(dǎo)入ANSYS二次開發(fā)程序后的計(jì)算模塊分析當(dāng)lx保持不變時(shí)尺寸因子g對(duì)高階連續(xù)懸臂梁的自由端撓度的影響。構(gòu)建一維懸臂梁，集中力P=10 N作用在懸臂梁自由端，梁長(zhǎng)度為5 mm，截面高度h=1 mm，厚度b=0.01 mm，橫截面面積A=h×b，彈性模量E=1.05×105MPa(面本征尺寸因子lx=2.5)，見圖3。

表4 尺寸因子g變化時(shí)對(duì)懸臂梁自由端撓度值 mm

g0.51.01.52.55.07.510.012.515.0w4.76344.75894.75194.72904.62464.46094.25064.00833.7478注:g為體本征尺寸因子;w為懸臂梁自由端撓度

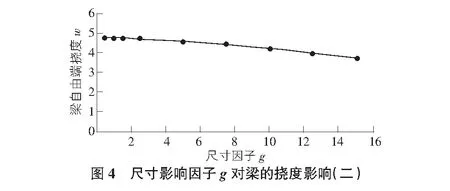
由表4數(shù)據(jù)可以看出，導(dǎo)入ANSYS二次開發(fā)的程序后，高階連續(xù)懸臂梁自由端撓度受到體本征尺寸因子g值的變化影響，且懸臂梁自由端撓度值變化趨勢(shì)隨g值的增大而減小(如圖4所示)。對(duì)比圖2與圖4可知梁撓度值的變化趨勢(shì)基本一致。

4 結(jié)語

基于ANSYS為用戶提供的APDL和UPFs二次開發(fā)工具，通過研究高階連續(xù)理論在有限元軟件中的應(yīng)用，得出以下結(jié)論：1)利用ANSYS提供的UELMatx.F用戶子程序，將高階連續(xù)理論及尺寸因子的概念引入到ANSYS中，實(shí)現(xiàn)高階連續(xù)梁在有限元軟件中的應(yīng)用，克服有限元軟件對(duì)高階連續(xù)結(jié)構(gòu)數(shù)值模擬的局限性，并得出尺寸因子的影響趨勢(shì)。2)計(jì)算結(jié)果與基于移動(dòng)最小二乘法框架的Fortran數(shù)值計(jì)算結(jié)果基本一致，通過算例驗(yàn)證了該方法的合理性、可行性。3)證明該方法對(duì)移動(dòng)最小二乘法在有限元軟件中應(yīng)用的可行性，為高階連續(xù)理論在有限元軟件中的應(yīng)用提供新思路。

[1] Xia Z C,Hutchinson J W.Crack tip fields in strain gradient plasticity[J].Journal of the Mechanics & Physics of Solids,1996,44(10):1621-1648.

[2] Fleck N A,Hutchinson J W.Strain Gradient Plasticity[J].Advances in Applied Mechanics,1997(33):295-361.

[3] Toupin R A.Elastic materials with couple-stresses[J].Archive for Rational Mechanics and Analysis,1962,11(1):385-414.

[4] 梁醒培,王 輝.應(yīng)用有限元分析[M].北京：清華大學(xué)出版社,2010.

[5] Belytschko T,Krongauz Y,Organ D,et al.Meshless methods:An overview and recent developments[J].Computer Methods in Applied Mechanics & Engineering,1996,139(1-4):3-47.

[6] Belytschko T,Lu Y Y,Gu L.Element-Free Galerkin methods[J].International Journal for Numerical Methods in Engineering,1994,37(2):229-256.

[7] 李 雷,謝水生,黃國(guó)杰.應(yīng)變梯度塑性理論下超薄梁彎曲中尺度效應(yīng)的數(shù)值研究[J].工程力學(xué),2006,23(3):44-48.

[8] 李 莉,陳萬吉,鄭 楠.修正偶應(yīng)力理論層合薄板穩(wěn)定性模型及尺度效應(yīng)[J].工程力學(xué),2013,30(5):1-7.

[9] Sun Y,Liew K M.The buckling of single-walled carbon nanotubes upon bending:The higher order gradient continuum and mesh-free method[J].Computer Methods in Applied Mechanics & Engineering,2008,197(33-40):3001-3013.

[10] Sun Y,Liew K M.Application of the higher-order Cauchy-Born rule in mesh-free continuum and multiscale simulation of carbon nanotubes[J].International Journal for Numerical Methods in Engineering,2010,75(10):1238-1258.

[11] 師 訪.ANSYS二次開發(fā)及應(yīng)用實(shí)例詳解[M].北京：中國(guó)水利水電出版社,2012.

[12] 張 雄,劉 巖.無網(wǎng)格法(精)[M].北京：清華大學(xué)出版社,2004.