起重機箱形梁貫穿裂紋尖端前沿形狀簡化研究

羅友紅，吳 曉，丁正男，楊海艷

（西南交通大學 機械工程學院，四川 成都 610031）

1 引言

箱形梁作為一種體積較大的焊接結構，在生產、焊接、使用過程中不可避免的存在夾渣、氣孔、裂紋等缺陷。這些缺陷在疲勞載荷作用下，逐漸萌生出裂紋，然后擴展直至斷裂。箱形梁作為橋門式起重機的主要承載構件，長期受到交變載荷的作用，因疲勞而引發的失效和斷裂是其主要的破壞形式。而斷裂往往是突然發生的，會導致不可預知的事故，往往會造成巨大的人身傷害和經濟損失。從起重機服役安全的角度，對含有裂紋缺陷的起重機箱形梁進行斷裂研究具有重要工程實用價值。

文獻[1-2]利用有限元軟件ANSYS建立了含裂紋缺陷的起重機箱形梁模型，并用奇異單元計算出裂紋尖端的應力強度因子，用于箱形梁的剩余強度計算以及疲勞壽命預測。文獻[3]中對Q345B非標準箱形梁試件，進行了疲勞裂紋擴展實驗，并運用有限元計算應力強度因子，用于指導含裂紋缺陷的起重機結構安全評價。文獻[4]基于ANSYS的Shell-Solid子模型技術，建立了起重機箱形梁的裂紋子模型，深入分析了裂紋尺度，結構參數對斷裂參數的影響。

對含裂紋缺陷的結構進行斷裂分析，首先得對實際裂紋進行規則化處理。各國有關行業標準中，比如BS7910，GBT19624-2004等，對裂紋缺陷的規則化處理有介紹。以往對于起重機箱形梁的貫穿裂紋，常常被簡化成等長矩形裂紋，而根據實際檢測和疲勞試驗[5]，起重機箱形梁下蓋板與腹板上的貫穿裂紋，其上下裂紋邊不等長。文獻[6]對含貫穿斜裂紋的平板進行斷裂分析，得出當平板遠端受拉應力時，斜裂紋可以簡化成等長裂紋，而當平板遠端加上彎矩作用時，斜裂紋不能簡化成等長裂紋。由于箱形梁結構及其受力情況復雜，對于其貫穿裂紋的簡化成處理成等長裂紋的合理性需進一步研究驗證。36t集裝箱門式起重機箱形梁整體結構為研究對象，利用有限元分析軟件Abaqus對箱形梁整體結構進行有限元分析，再利用子模型技術建立不同裂紋簡化形狀的有限元子模型，并采用相互作用積分法分別計算不同裂紋形狀下裂紋尖端的應力強度因子KI。分析比較KI的值，驗證貫穿裂紋簡化處理成等長裂紋的合理性，為起重機箱形梁結構進行斷裂分析提供依據。

2 裂紋位置及形狀簡化

根據對在役起重機箱形梁的實際檢測和疲勞試驗，發現其疲勞裂紋主要出現在下蓋板與主腹板間的縱向受拉翼緣焊縫上，裂紋從焊縫內圓形缺陷的圓心開始向下蓋板和腹板擴展穿透板厚；以及出現在大隔板與主腹板連接焊縫下端的焊趾處，裂紋由多個表面橢圓裂紋源匯合形成腹板穿透裂紋。考慮裂紋的危險程度，主要研究箱形梁跨中下蓋板與主腹板翼緣焊縫上形成的穿透裂紋，其形成擴展，如圖1所示。以往對于箱形梁下蓋板上出現的穿透裂紋，為了便于分析計算常常將其簡化成形狀簡單的等長裂紋，即用一條過下蓋板下邊長裂紋尖端點的豎直直線代替實際裂紋前沿；而實際裂紋在下蓋板上下邊的長度是不相等的。由于下蓋板受力不均勻，下蓋板下邊的裂紋長度要大于其上邊的裂紋長度。因此，可以用一條過下邊裂紋尖端點的斜線來模擬實際裂紋尖端前沿，如圖2所示。通過改變斜線的傾角β，模擬不同的實際裂紋，隨之也得到不同的簡化等長裂紋，并分別計算比較斜線裂紋尖端與簡化等長裂紋尖端的應力強度因子值。

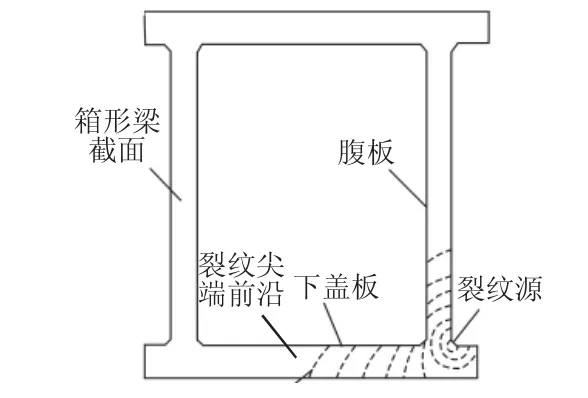
圖1 下蓋板—腹板焊縫處裂紋起源擴展示意圖Fig.1 Schematic Diagram of Crack Initiation and Propagation in the Weld of the Bottom Plate and Web Plate

圖2 裂紋尖端前沿形狀簡化圖Fig.2 Simplified Diagram of the Front Shape of Crack Tip

3 計算應力強度因子

目前已經提出許多方法用于應力強度因子的計算，比如邊界元法、解析法、有限元法、混合法、權函數法等。有限元法由于其強大的模擬和數值計算功能已被廣泛用于復雜結構應力強度因子的計算。文獻[7]研究比較了不同計算應力強度因子KI的數值方法，其中相互作用積分法得到了較為準確的計算結果。因此，裂紋尖端的應力強度因子采用相互作用積分法來計算。

相互作用積分法是在J積分的基礎上提出的。J積分的表達式如下[8]

式中：τ—圍繞裂尖的任意閉合積分路徑；W—應變能密度；T—張力矢量；u—位移矢量；s—弧長。

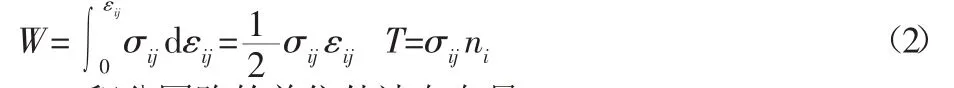
式中：ni—積分回路的單位外法向向量。

式中：I—真實場與輔助場的相互作用積分。

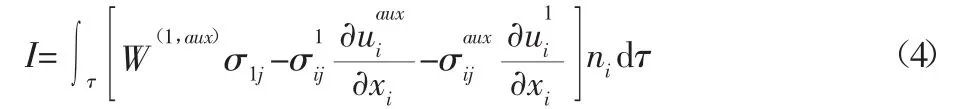
在線彈性情況下，J積分與應變能釋放率G和應力強度因子存在如下關系[9]：

式中：E和υ—裂紋尖端處的彈性模量和泊松比。

由上述幾式類似得到相互作用積分為：

4 有限元計算分析

4.1 箱形梁整體結構有限元計算

以某鐵路局36t集裝箱門式起重機箱形梁為研究對象，其主要結構參數為跨度18m，懸臂長12.5m，小車軸距8.6m。先在Solidworks中建立三維模型，然后導入有限元分析軟件Abaqus中，采用四面體Tet單元劃分網格建立有限元模型，如圖3所示。為研究箱形梁跨中位置的裂紋，將小車位于跨中，起升機構滿載提升（考慮沖擊載荷）時，作為最危險工況。同時考慮箱形梁自重、風載、大車運行偏斜側向力等的作用。在最危險工況下，箱形梁結構的等效應力云圖，如圖4所示。最大應力出現在支腳連接結構上；跨中位置的裂紋受力情況較為復雜。

圖3 箱形梁整體結構有限元模型Fig.3 Finite Element Model of Box Girder Structure

圖4 箱形梁整體結構等效應力云圖Fig.4 The Equivalent Stress Distribution of Box Girder Structure

4.2 裂紋子模型有限元分析

為了對箱形梁跨中位置的貫穿裂紋進行精確和高效的分析，采用子模型分析技術。即在前面箱形梁整體結構模型和分析結果的基礎上，截取箱形梁跨中附近的部分腹板和下蓋板，并在下蓋板與腹板的相應位置處嵌入貫穿裂紋，進而對裂紋形狀進行重點分析研究。子模型相對箱形梁整體結構模型的位置，如圖5所示。

圖5 子模型結構位置示意圖Fig.5 Schematic Diagram of the Position of the Sub Model Structure

在子模型上嵌入斜裂紋來模擬實際裂紋，網格劃分時需對裂紋尖端前沿進行特殊處理，實現裂紋尖端的奇異性，斜裂紋子模型的有限元模型，如圖6所示。子模型中斜裂紋的參數如圖2中所示，其中 as=30mm，a′s=10mm，al與 a′l的值與 β 取值有關，而 β分別取45°，60°，75°來模擬不同形狀的斜裂紋。根據不同的β值，相應的可以得到不同的簡化等長裂紋。按照同樣的網格處理方法，得到簡化等長裂紋的有限元模型，如圖7所示。

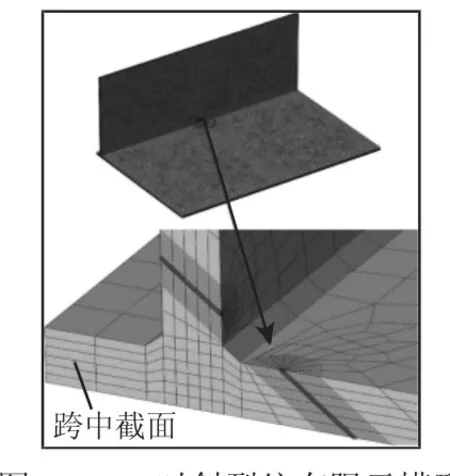
圖6 β=45°時斜裂紋有限元模型Fig.6 Finite Element Model of Oblique Crack when β=45°

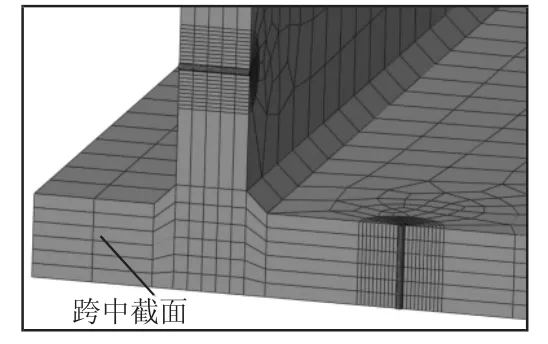
圖7 β=45°時簡化等長裂紋有限元模型Fig.7 Finite Element Model of Simplified Equal Length Crack when β=45°

4.2.1 裂紋模型有限元計算

根據箱形梁整體結構分析結果，將整體模型在子模型邊界上的位移結果，插值到子模型的切割邊界上，作為裂紋子模型的邊界約束條件。通過有限元計算，得到斜裂紋子模型和相應簡化等長裂紋的等效應力云圖，如圖8和圖9所示。通過觀察分析結果，發現在斜裂紋情況下，短側裂紋端的應力比長側裂紋端更為集中，因而短裂紋要比長裂紋先開裂。這與實際裂紋的擴展情況相符；在簡化等長裂紋情形下，位于下蓋板下邊的裂紋端以及腹板外側的裂紋端處的應力相對更為集中，因而這兩處的裂紋尖端先開裂，這證明了斜裂紋設定的方向是合理的。

圖8 β=45°時斜裂紋子模型等效應力云圖Fig.8 The Equivalent Stress Distribution of Oblique Crack when β=45°

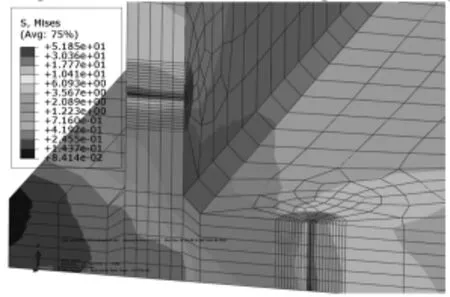
圖9 β=45°時簡化等長裂紋子模型等效應力云圖Fig.9 The Equivalent Stress Distribution of Simplified Equal Length Crack when β=45°

4.2.2 KI的計算比較分析

基于子模型技術，建立不同參數下的斜裂紋和相應的簡化等長裂紋，并采用相互作用積分法計算得到各裂紋尖端前沿的應力強度因子KI的值結果，如圖10和圖11所示。從圖10和圖11中的計算結果可以看出，斜裂紋中，短側裂紋端的應力強度因子明顯大于長側裂紋端，并且隨著斜裂紋傾角β值的增大，短側裂紋端的應力強度因子值減小，而長側裂紋端的應力強度因子值卻增大；在簡化等長裂紋中，下蓋板上裂紋尖端前沿的應力強度因子值沿著厚度方向從上邊至下邊逐漸增大，而在腹板上，裂紋尖端的應力強度因子值沿著厚度方向從內側至外側也逐漸增大，這與下蓋板和腹板的受力情況相符合。通過將KI的值進行比較可知，簡化等長裂紋尖端前沿的最大應力強度因子值總是比斜裂紋尖端的應力強度因子值大。因此，將斜裂紋簡化成等長裂紋是合理可行的。

圖10 下蓋板上不同裂紋尖端前沿KI的比較Fig.10 Comparison of KIwith Different Crack Tip at the Bottom Plate

圖11 腹板上不同裂紋尖端前沿KI的比較Fig.11 Comparison of KIwith Different Crack Tip at the Web Plate

5 結論

運用有限元分析軟件Abaqus建立了起重機箱形梁的整體有限元模型和裂紋子模型，采用相互作用積分法分別計算了箱形梁下蓋板和腹板上，不同形狀參數下的貫穿斜裂紋以及相應簡化等長裂紋尖端的應力強度因子KI。通過將KI值進行比較分析，證實了將起重機箱形梁中的實際裂紋簡化成等長裂紋進行斷裂分析是合理可行的。

［1］李振華.起重機金屬結構疲勞壽命預測與疲勞可靠性研究［D］.成都：西南交通大學，2009（Li Zhen-hua.Study on fatigue life prediction and fatigue reliability of the metalstructureofcrane［D］.ChengDu：SouthwestJiaotongUniversity，2009.）

［2］時磊，吳曉，黃瀚.服役起重機箱型梁結構三維裂紋應力強度因子的有限元模擬［J］.機械設計與制造，2013（7）：199-202.（Shi Lei，Wu Xiao，Huang Han.The simulation of stress intensity factor of 3D crack of girder of existing crane with FEM［J］.Machinery Design&Manufacture，2013（7）：199-202.）

［3］李中金.港口起重機帶裂紋結構安全評價實驗及應用研究［D］.武漢：武漢理工大學，2014.（Li Zhong-jin.The experimental and applied research onsafety assessment for metal structures with initial crack onport crane［D］.Wuhan：Wuhan University of Technology，2014.）

［4］熊剛，吳曉，羅友紅.含缺陷起重機箱形梁結構斷裂分析與有限元仿真［J］.機械設計與制造，2016（4）：207-210.（Xiong Gang，Wu Xiao，Luo You-hong.Fracture analysisand finite element simulation of crane box girder structure containing defects［J］.Machinery Design&Manufacture，2016（4）：207-210.）

［5］潘長松.橋式起重機箱形主梁的疲勞性能［J］.起重運輸機械，1984（1）：17-28.（Pan Chang-song.Property of box girders of overhead type crane［J］.Hoisting and Conveying Machinery，1984（1）：17-28.）

［6］高小勤，黃海明，章梓茂.貫穿斜裂紋應力強度因子的計算［J］.科學技術與工程，2006，6（3）：293-295.（Gao Xiao-qin，Huang Hai-ming，Zhan Zi-mao.Calculation of stress intensity factors for oblique through cracks［J］.Science Technology and Engineering，2006，6（3）：293-295.）

［7］Qian G，González-Albuixech V F，Niffenegger M.Comparison of KI calculation methods［J］.Engineering Fracture Mechanics，2016（156）：52-67.

［8］Rice J R.A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks［J］.Journal of Applied Mechanics，1967，35（2）：379-386.

［9］Brian Lawn.脆性固體斷裂力學［M］.北京：高等教育出版社，2010.（Brian Lawn.Fracture of Brittle Solids［M］.Beijing：Higher Education Press，2010.）