核極化的核參數(shù)選擇算法

張文興，陳肖潔，王建國(guó)

（內(nèi)蒙古科技大學(xué) 機(jī)械工程學(xué)院，內(nèi)蒙古 包頭 014010）

1 引言

支持向量機(jī)（support vector machine，SVM）是在1992年的計(jì)算學(xué)習(xí)理論會(huì)議上由文獻(xiàn)[1]引進(jìn)機(jī)器學(xué)習(xí)領(lǐng)域的新一代智能算法。SVM廣泛應(yīng)用于模式識(shí)別和回歸估計(jì)，如金屬結(jié)構(gòu)安全評(píng)估[2]、鉚接力的回歸預(yù)測(cè)[3]。SVM是基于核的學(xué)習(xí)機(jī)器，其核心是通過(guò)核函數(shù)隱式定義非線性變換，即不必顯式地計(jì)算從輸入空間到高維特征空間的非線性變換，而是在高維特征空間中隱式地高效計(jì)算內(nèi)積。顯然，通過(guò)核函數(shù)所構(gòu)建的核矩陣包含了訓(xùn)練數(shù)據(jù)和高維特征空間隱含的信息，SVM的泛化能力在很大程度上依賴于核函數(shù)的確定，而核參數(shù)直接影響著核函數(shù)的構(gòu)建。因而，選擇一個(gè)適當(dāng)?shù)暮藚?shù)是求解的第一步。

目前，常用的參數(shù)選擇方法有以下幾種：（1）根據(jù)問(wèn)題的先驗(yàn)信息來(lái)選擇參數(shù)，但該方法僅對(duì)一些特殊問(wèn)題如圖像識(shí)別有效，并不適用于一般問(wèn)題；（2）k-折交叉驗(yàn)證法[4]（在實(shí)際應(yīng)用中10折交叉驗(yàn)證應(yīng)用最廣）是參數(shù)選擇經(jīng)典的方法，其本質(zhì)是用參數(shù)空間中每一組可能的參數(shù)組合去訓(xùn)練和測(cè)試SVM，找出效果最好的參數(shù)組合，其特點(diǎn)是經(jīng)驗(yàn)性強(qiáng)，計(jì)算量大，且不適用于優(yōu)化參數(shù)多于兩個(gè)的情況；（3）通過(guò)梯度下降法最小化泛化誤差來(lái)進(jìn)行多參數(shù)選取[5]，但該方法需要迭代求解對(duì)偶問(wèn)題，計(jì)算量較大；（4）一些精度較高，但計(jì)算復(fù)雜性也較高的優(yōu)化算法，如基于Bayesian方法；（5）基于優(yōu)化核度量標(biāo)準(zhǔn)的方法，其主要出發(fā)點(diǎn)是如何衡量核函數(shù)和學(xué)習(xí)任務(wù)（分類）的一致性[6]。其基礎(chǔ)是一系列獨(dú)立于算法的核度量標(biāo)準(zhǔn)的提出，如核排列（kernelalignment）[7-8]、核極化（kernelpolarization）[9]等。核度量標(biāo)準(zhǔn)著力于捕捉訓(xùn)練數(shù)據(jù)集在高維特征空間中的可分離特性，在不考慮核函數(shù)計(jì)算復(fù)雜度的前提下，計(jì)算復(fù)雜度為o（l2），其中，l是訓(xùn)練樣本的個(gè)數(shù)，因而計(jì)算是高效率的。遵循上述核度量標(biāo)準(zhǔn)的思路，將核極化直接最大化算法應(yīng)用于Gaussian核和Polynomial核的核參數(shù)的選擇中，以使多類SVM獲得更好的分類性能。

2 支持向量機(jī)（SVM）

2.1 二分類SVM提出及求解

樣本集 D=（xi，yi），xi∈Rn，yi∈｛+1，-1｝，i=1，…，l，能將 D正確地分為兩類的最優(yōu)分類超平面＜ω·x＞+b=0的求解等價(jià)于解l1-SVM或C-SVM，其原始問(wèn)題為：

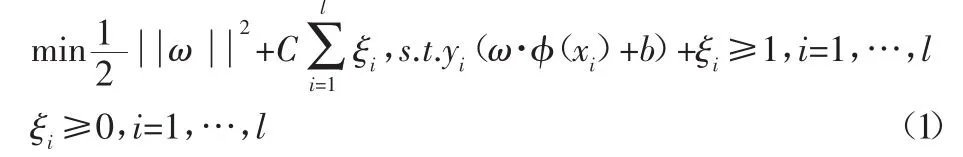
式中：C—正則化參數(shù)（權(quán)衡調(diào)和最大化平面間隔和最小化訓(xùn)練錯(cuò)誤兩個(gè)目標(biāo)）；ξi—松弛變量；φ（x）—從輸入空間到高維特征空間的映射。

拉格朗日乘子法求解（1）式，得到Wolfe對(duì)偶問(wèn)題：

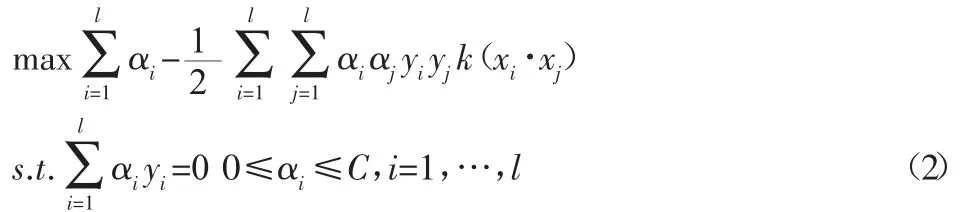
式中：αi—拉格朗日乘子，解中αi≠0所對(duì)應(yīng)的xi稱為支持向量，即對(duì)最優(yōu)分類超平面有貢獻(xiàn)的樣本，αi≠0稱為支持向量值。解上述優(yōu)化問(wèn)題（2）可以得到如下決策函數(shù)：

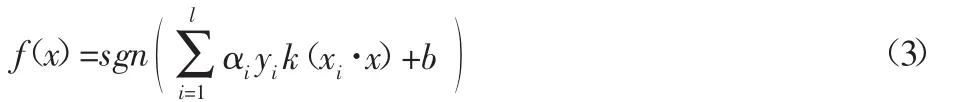
2.2 多分類SVM的求解

多分類SVM的求解主要分為兩種[10]：（1）將多分類問(wèn)題轉(zhuǎn)化為二分類問(wèn)題，如one-versus-rest（1-v-r）和one-versus-one（1-v-1）算法；（2）用一個(gè)最優(yōu)化問(wèn)題一次求解所有的超平面實(shí)現(xiàn)多分類分類。1-v-r算法：此方法簡(jiǎn)單、有效，但當(dāng)類別較大時(shí)，某一類的訓(xùn)練樣本將大大少于其他類訓(xùn)練樣本的總和，這種訓(xùn)練樣本間的不均衡將明顯地影響測(cè)試精度。1-v-1算法：測(cè)試時(shí)采用投票法，類別輸出為得票數(shù)最多的那一類，在實(shí)際應(yīng)用中，一般推薦使用1-v-1方法。而對(duì)于在一個(gè)最優(yōu)化問(wèn)題中求解多個(gè)分類面的參數(shù)的方法，乍看起來(lái)簡(jiǎn)潔快捷高效，但是在實(shí)際操作過(guò)程中，過(guò)多的變量和過(guò)于復(fù)雜的目標(biāo)函數(shù)導(dǎo)致過(guò)高的計(jì)算復(fù)雜度，在分類準(zhǔn)確率上也毫無(wú)優(yōu)勢(shì)可言。因此，該算法在實(shí)際問(wèn)題中并不適用。

3 核函數(shù)

在SVM中，核函數(shù)的構(gòu)造和選擇尤其重要。在滿足Mercer條件的情況下，在SVM理論研究與實(shí)際應(yīng)用中，最常使用的有以下4類基本核函數(shù)：線性核、多項(xiàng)式核、Gaussian核和Sigmoid核。采用Polynomial核和Gaussian核，其形式如下：

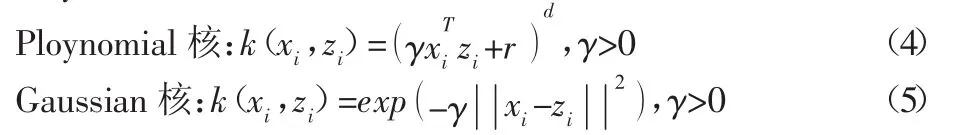
式中：γ、r、d—核參數(shù)。

4 核極化及核參數(shù)選擇算法

Baram在2005年，針對(duì)于二分類問(wèn)題，提出了一種核函數(shù)度量標(biāo)準(zhǔn)—核極化，核極化體現(xiàn)了核矩陣G與理想核矩陣yyT之間的相似度，其形式為：

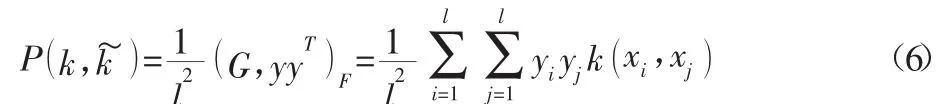
式中：y=（y1，…yi）T，G—核矩陣，即是理想核矩陣，＜·，·＞F表示具有同樣維數(shù)的一對(duì)矩陣之間的Frobenius內(nèi)積。針對(duì)多分類問(wèn)題，文獻(xiàn)[9]提出了一個(gè)新的適應(yīng)于多分類（也適應(yīng)二分類）情形的核函數(shù)度量標(biāo)準(zhǔn)：

式（7）清楚地顯示，核極化是一個(gè)標(biāo)量值，其值越大意味著在特征空間中同類的數(shù)據(jù)點(diǎn)相互靠近，而異類的數(shù)據(jù)點(diǎn)相互遠(yuǎn)離[9]。P可以度量多分類樣本的可分性，P值越大說(shuō)明其數(shù)據(jù)集樣本在設(shè)定的核函數(shù)下具有越好的可分性，以此建立的SVM模型，具有越強(qiáng)的泛化能力。值得關(guān)注的另一點(diǎn)是，其計(jì)算復(fù)雜度為O（l2），具有高效計(jì)算性。采用核極化P來(lái)指導(dǎo)Gaussian核和Polynomial核的核參數(shù)的選擇，選擇使得Pmax（γ）的γ值，此時(shí)，γ值對(duì)應(yīng)的最大值P說(shuō)明其數(shù)據(jù)集樣本在該γ值時(shí)具有較好的可分性。較優(yōu)γ值的選取我們采用網(wǎng)格搜索法，其算法步驟如下：（1）（初始化）核函數(shù)的 Pmax及 γ 值，設(shè)置 γ1=γmin=2-8，γmax=28，r=1，d=3；（2）（迭代）對(duì)于每一個(gè) γi=γi-1·4，計(jì)算其對(duì)應(yīng)的 Pi；（3）若 Pi≥Pmax時(shí)，更新 Pmax和γ值；（4）轉(zhuǎn)到第2步，直到滿足停機(jī)條件。實(shí)驗(yàn)對(duì)應(yīng)的算法流程圖，如圖1所示。

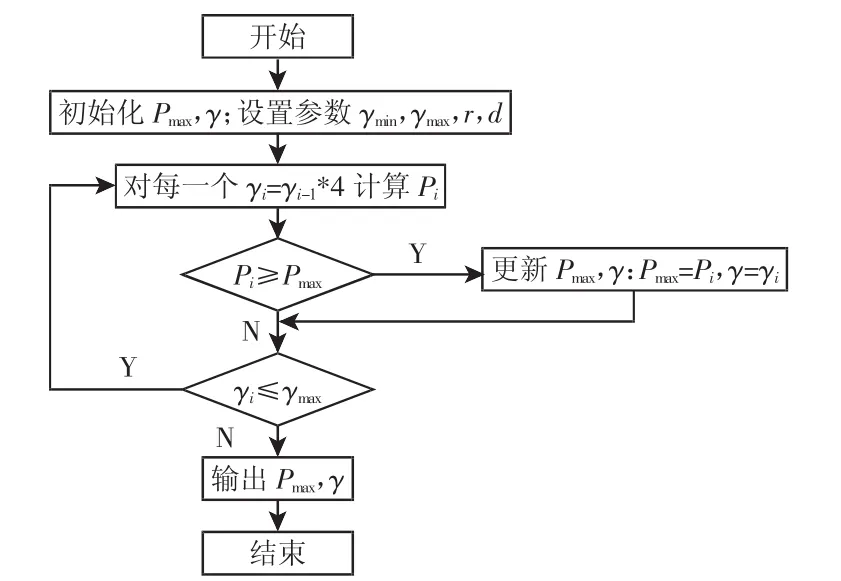
圖1 核參數(shù)選擇算法流程圖Fig.1 The Flow Chart of Kernel Parameter Selection Algorithm

5 實(shí)驗(yàn)

5.1 數(shù)據(jù)處理

UCI數(shù)據(jù)庫(kù)中的 7 個(gè)數(shù)據(jù)集：Breast Cancer Wisconsin，Iris，Wine，Car，glass，Zoo，Balance。其中 Breast Cancer Wisconsin 為二分類數(shù)據(jù)集，其余均為多分類數(shù)據(jù)集。數(shù)據(jù)集的基本情況，如表1所示。每個(gè)數(shù)據(jù)集都經(jīng)過(guò)歸一化（0，1）預(yù)處理，即：

式中：i—樣本的某個(gè)輸入特征。選取總樣本數(shù)的70%為訓(xùn)練集和30%為測(cè)試集，采用libsvm軟件包（該軟件包采用1-v-1的方法）實(shí)現(xiàn)了多類SVM分類。

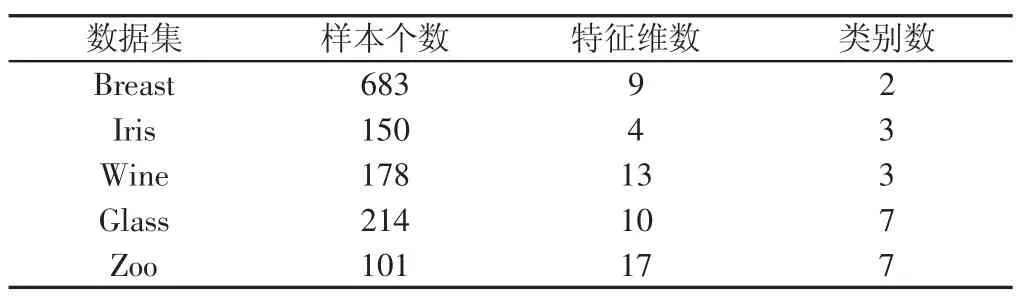
表1 實(shí)驗(yàn)使用的數(shù)據(jù)集Tab.1 Data Sets for Experiments

5.2 評(píng)價(jià)指標(biāo)

實(shí)驗(yàn)中選用分類正確率（又稱為分類精度）作為算法的評(píng)價(jià)指標(biāo)。其表達(dá)式為Acc=Cor/Tot，Cor為分類正確的樣本點(diǎn)數(shù)，Tot為總樣本點(diǎn)數(shù)，Acc為分類正確率。

5.3 實(shí)驗(yàn)方法

設(shè)置Gaussian核和Polynomial核的核參數(shù)γ的取值范圍為γmin=2-8，γmax=28。首先，利用前面所介紹的核參數(shù)選擇方法，選擇出Pmax（γ）的γ值。然后，用選擇出的γ和設(shè)置懲罰系數(shù)C=80，訓(xùn)練和測(cè)試SVM。為驗(yàn)證所提出基于核極化的核參數(shù)選擇算法的有效性，選擇目前SVM最常用經(jīng)典的10折交叉驗(yàn)證法作為比較。設(shè)置懲罰系數(shù) C=｛2-8，2-6，…，28｝和 γ=｛2-8，2-6，…，26，28｝，利用 10折交叉驗(yàn)證法選擇出最優(yōu)參數(shù)組合和進(jìn)行測(cè)試。所有實(shí)驗(yàn)的平臺(tái)為Intel（R）Core（TM）2 Duo CPU E8200@2.66GHz 2.00GB RAM的個(gè)人計(jì)算機(jī)，Win732位操作系統(tǒng)。實(shí)驗(yàn)流程圖，如圖2所示。

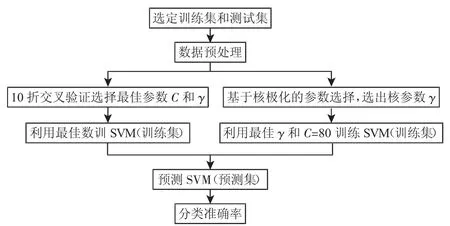
圖2 實(shí)驗(yàn)方法流程圖Fig.2 The Flow Chart of Experimental Methods

5.4 實(shí)驗(yàn)結(jié)果及其分析

實(shí)驗(yàn)方法的多類SVM分類準(zhǔn)確率的平均值（采用10次實(shí)驗(yàn)的平均值），如表2所示。對(duì)應(yīng)于表2各數(shù)據(jù)集實(shí)驗(yàn)結(jié)果的運(yùn)行時(shí)間，如表3所示。

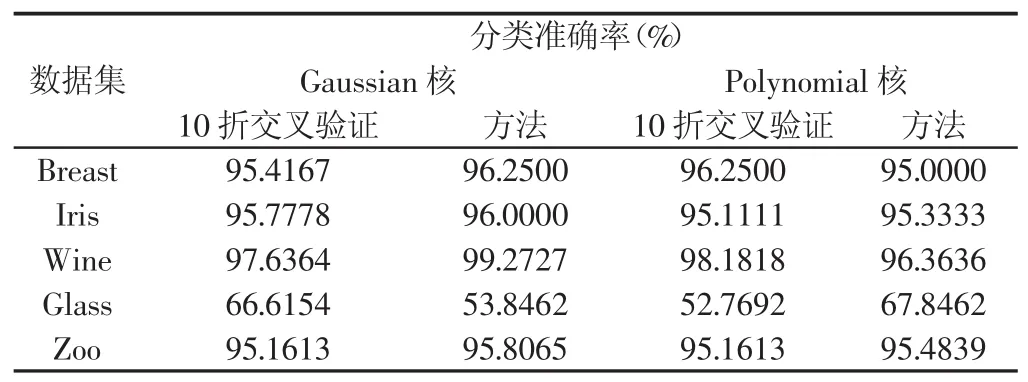
表2 數(shù)據(jù)集上的實(shí)驗(yàn)結(jié)果Tab.2 Experimental Results of Data Sets

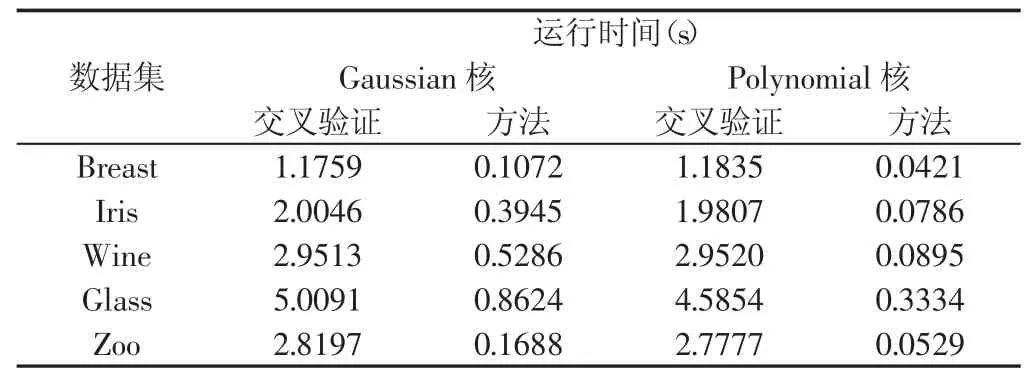
表3 實(shí)驗(yàn)結(jié)果的運(yùn)行時(shí)間Tab.3 Running Time of Experimental Results

表2的2～3列或4～5列的數(shù)據(jù)顯示，對(duì)于Gaussian核或Polynomial核采用方法的SVM的泛化能力并不弱于10折交叉驗(yàn)證法，大部分?jǐn)?shù)據(jù)集的準(zhǔn)確率高于10折交叉驗(yàn)證法。表3說(shuō)明采用方法計(jì)算的高效性。表2的第2列與第4列和第3列與第5列說(shuō)明，只有一個(gè)核參數(shù)r的Gaussian核比有三個(gè)核參數(shù)的Polynomial核在分類方面具有更高的準(zhǔn)確率，但是，不可忽視的是，在分類準(zhǔn)確率上略遜于Gaussian核的Polynomial核的運(yùn)行時(shí)間遠(yuǎn)小于Gaussian核。以上分析說(shuō)明，所提出的基于核極化的核參數(shù)選擇算法的有效性，計(jì)算的高效性。同時(shí)，也說(shuō)明了Polynomial核雖然沒(méi)有Gaussian核的調(diào)整核參數(shù)少，分類精度高等優(yōu)點(diǎn)，但是其運(yùn)行速度的高效性也同樣值得我們關(guān)注。

6 結(jié)論

在深入分析核極化這個(gè)核度量標(biāo)準(zhǔn)的基礎(chǔ)上，提出了利用直接最大化核極化來(lái)選擇核參數(shù)值的算法，并將其運(yùn)用到Gaussian核和Ploynomial核的核參數(shù)r選擇中，提升了多類SVM的分類性能。在整個(gè)核函數(shù)的核參數(shù)選擇過(guò)程中無(wú)須反復(fù)地訓(xùn)練和測(cè)試SVM，也不需要求解一個(gè)額外的、復(fù)雜的二次規(guī)劃問(wèn)題，因而計(jì)算是高效的。

［1］Boser B E，Guyon I M，Vapnik V N.A training algorithm for optimal margin classifiers［C］.5th Annual ACM Conference on Computational Learning Theory.Pittsburgh，PA，ACM Press，1992：144-152.

［2］舒文杰，徐桂芳，魏國(guó)前.SVM的起重機(jī)金屬結(jié)構(gòu)安全評(píng)估研究［J］.機(jī)械設(shè)計(jì)與制造，2014（12）：269-272.（Shu Wen-jie，Xu Gui-fang，Wei Guo-qian.Metal structure safety assessment of crane based on SVM［J］.Machinery Design＆Manufacture，2014（12）：269-272.）

［3］陳健飛，蔣剛，楊劍鋒.改進(jìn)ABC-SVM的參數(shù)優(yōu)化及應(yīng)用［J］.機(jī)械設(shè)計(jì)與制造，2016（1）：24-28.（Chen Jian-fei，Jiang Gang，Yang Jian-feng.Improved ABC-SVM parameter optimizationand application［J］.MachineryDesign ＆ Manufacture，2016（1）：24-28.）

［4］Duan K B，Keerthi S S，Poo A N.Evaluation of simple performance measures for tuning SVM hyperparameters［J］.Neurocomputing，2003（51）：41-59.

［5］常群，王曉龍，林沂蒙.支持向量分類和多寬度高斯核［J］.電子學(xué)報(bào)，2007，35（3）：484-487.（Chang Qun，Wang Xiao-long，Lin Qi-meng.Support vector classification and Gaussain kernel with multiple widths［J］.Acta Electronica Sinica，2007，35（3）：484-487.）

［6］汪廷華，陳峻婷.核函數(shù)的度量研究進(jìn)展［J］.計(jì)算機(jī)應(yīng)用研究，2011，28（1）：25-28.（Wang Ting-hua，Chen Jun-ting.Survery of research on kernel function evaluation［J］.Application Research of Computers，2011，28（1）：25-28.）

［7］Cortes C，Mohri M，Rostamizadeh A.Algorithms for learning kernel based on centered alignment［J］.J Mach Learn Res，2012（13）：795-828.

［8］Wang Ting-hua，Zhao Dong-yan，Tian Shen-feng.An overview of kernel alignment and its applications［J］.Artif Intell Rev，2015（43）：149-192.

［9］汪廷華，趙東巖，張瓊.多類核極化及其在多寬度RBF核參數(shù)選擇中的應(yīng)用［J］.北京大學(xué)學(xué)報(bào)：自然科學(xué)版，2012，48（5）：727-731.（Wang Ting-hua，Zhao Dong-yan，Zhang Qiong.Multiclass kernel polarization and its application to parameter selection of RBF kernel with multiplewidths［J］.ActaScientiarumNaturaliumUniversitatisPekinensis，2012，48（5）：727-731.）

［10］Hsu C W，Lin C J.A comparison of methods for multiclass support vector machines［J］.IEEETransactions on Neural Networks，2002，13（2）：415-425.