磨加工主動測量儀在線圓度評定理論研究

賈英鋒，鄭 鵬，張琳娜，郭俊可

（鄭州大學 機械工程學院，河南 鄭州 450001）

1 引言

隨著現在制造技術的提高，人們對精密零件的加工、檢測要求也越來越高。磨加工主動測量儀是一種能夠在線檢測工件尺寸，并由測得尺寸變化值與設定信號點值做比較，進而對機床發出指令信號，控制機床動作的儀器，如圖1所示。主動測量能夠實現不停機測量和控制機床動作，可以降低工人勞動強度、提高生產效率，同時也可提高工件表面質量、產品一致性。磨削加工過程中，為了在保證工件表面質量的前提下提高加工效率，一般采用“粗磨—精磨—光磨”的三級加工模式，或者“粗磨—精磨—半精磨—光磨”四級加工模式，如圖2所示。顯然，在逐級加工模式下，工件的圓度是隨著加工進程而逐漸降低的。影響工件圓度的因素是復雜多樣的，其中一個重要因素是上一級加工過程中工件形成的圓度，工件已有的圓度通過工件與砂輪間的法向切削力的變化映射和影響到下一級加工過程的工件圓度。因此，對于工件圓度的檢測往往也希望能夠實現逐級檢測，而不是等待整個加工過程完成后機后檢測工件圓度。以常

見的“粗磨—精磨—光磨”的三級加工模式介紹磨加工主動量儀在同時檢測尺寸和圓度模式下的加工流程，如圖3所示。其中，工件為外徑時，尺寸信號點設定值 P1＞P2＞P3＞P4，其中 P4=0，即到尺寸。圓度信號點設定值 Y2＞Y3＞Y4，Y2、Y3、Y4分別為工件尺寸值到達 P2、P3、P4時要求達到的圓度值，其中Y4即最終圓度要求。

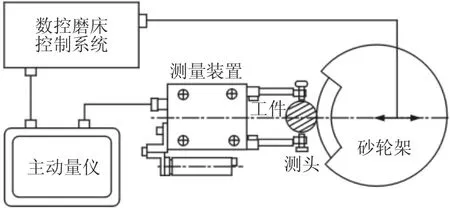
圖1 磨加工主動量儀Fig.1 Grinding Active Measuring Instrument

圖2 磨加工主動量儀“粗磨—精磨—光磨”模式Fig.2 The Mode of“Rough Grinding，Fine Grinding and Polishing”for Grinding Machine

圖中：P1、P2、P3、P4—主動測量控制器信號設定點；S1-S2—粗磨階段；S2-S3—精磨階段；S3—S4—光磨階段。

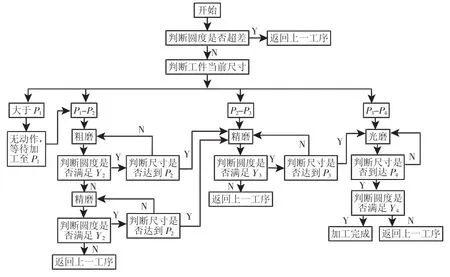
圖3 磨加工主動量儀檢測尺寸、圓度工作流程圖Fig.3 The Working Flow Chart of Measuring Dimension and Roundness of Grinding Machine

從磨加工主動測量對于尺寸、圓度的檢測工作流程中可以看出：圓度的在線檢測可以在加工過程中確定圓度不合格的工件，相比于機后圓度檢測可提高加工效率。磨削加工與圓度檢測同步進行的制造模式是必要的[1]。

目前，尺寸的主動測量已成為現有主動量儀最基本的功能，理論研究和技術應用都十分成熟。圓度在線評定方面，已經有學者做了一定的研究工作。文獻[2]設計了基于PMAC—PC下零件外圓表面磨削在線測量及加工系統；文獻[3]提出了基于IRM（改進反向法）和小波變換的圓度誤差在線檢測技術以實現主軸回轉誤差分離和環境噪聲消除；文獻[4]設計了一種基于LabView虛擬儀器技術的圓度誤差在線測量裝置；文獻[5]結合新一代GPS圓度誤差評定準則研究了磨加工主動測量儀在線圓度誤差評定技術及應用。但現有的在線圓度評定中“在線”基本上側重的是將圓度評定的硬件設備和軟件程序與加工設備相整合，也可以做到提高加工效率和一定的反饋控制。但是沒有考慮在線評定時加工進程對圓度的影響，在線圓度評定的原理與機后測量的圓度評定原理并無區別。因此，在考慮加工過程對在線圓度評定的影響基礎上，研究磨加工主動測量儀的在線圓度評定技術。

2 在線圓度評定技術

GB/T24632.1—2009中規定了四種圓度誤差評定方法[6]：最小二乘法、最小外接圓法、最大內切圓法和最小區域法。ISO/TC213發布的GPS規定[7]，切比雪夫擬合法也可以作為圓度誤差的評定方法。其中，最小區域法是圓度誤差的仲裁方法，計算精度高于其他方法，當其他方法出現爭議的時候，必須用最小區域法仲裁。最小外接圓法、最小內切圓法和最小區域法的算法難以簡單、快速確定擬合圓的圓心，一般通過移心算法實現，對于計算機編程而言較為復雜和困難。切比雪夫擬合法存在運算速度不高、初始值與算法關系的問題[6]。最小二乘法計算簡便，易于編程實現，可行性較高，故在實際應用中較為常見。對在線圓度的評定以最小二乘法為數學模型進行討論研究。

2.1 最小二乘法

圓的最重要信息在于圓心的位置和圓的半徑大小。最小二乘的擬合過程就是利用實際輪廓測得值確定擬合圓圓心和半徑值的過程。在圓度評定時，實際被測點的位置可以用極坐標（Ri，θi）表示，其中Ri是測點的極徑，θi是測點的極角，如圖4所示。將測點的極坐標轉化為直角坐標為：

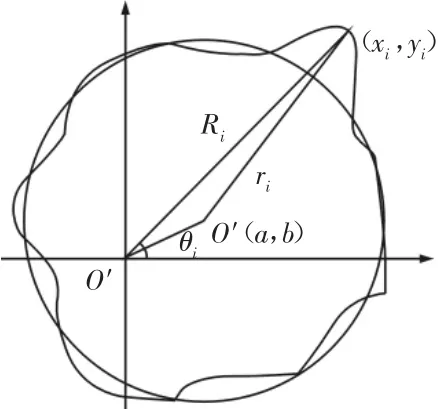
圖4 最小二乘數學模型示意圖Fig.4 Schematic Diagram of Least Squares Mathematical Model

設最小二乘圓的圓心坐標為（a，b），則相對于最小二乘圓心各實際測點的坐標和半徑分別為：最小二乘是使擬合圓半徑R與實測輪廓圓半徑的誤差的平方和為最小[8]。磨加工主動測量儀實際的圓度評定過程中，可以認為最小二乘圓的圓心與回轉類工件的回轉軸心十分接近，即a，b值極小。半徑誤差值 ei可近似表示為：ei=Ri-acosθi-bsinθi-R（i=1，2，…，m） （2）

同時，工件的圓度誤差與工件半徑相比是極小的。因此，由式（2）得：Ri=R+acosθi+bsinθ（ii=1，2，…，m） （3）

磨加工主動測量儀圓度評定時需要測量的點數m值很大，因此式（3）是一個超正定方程組。由文獻[9]可得：

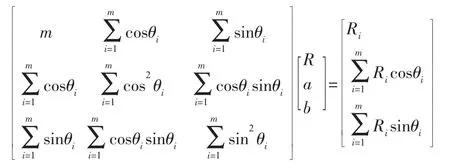
最小二乘圓法評定準則：以擬合最小二乘圓圓心為中心，作兩個同心圓包容實際被測輪廓，該輪廓上至少有一個測點與同心圓的內圓（外圓）相接觸。同心圓的半徑差即為最小二乘法所得圓度誤差[10]。設rmax、rmin為實際輪廓上測點至最小二乘圓心O′的最大半徑和最小半徑。則工件輪廓的最小二乘圓度誤差f為[5]：f=rmax-rmin（5）

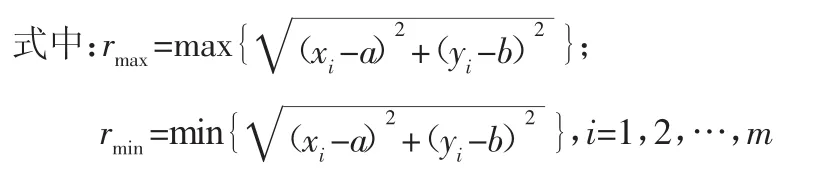
在主動測量儀測頭測得工件一周的測點極徑Ri和θi極角后，由式（1）、式（4）、式（5）即可計算得到最小二乘法圓度誤差評定結果。

2.2 在線圓度評定

應用最小二乘法進行圓度評定時，需要首先得到工件一周的輪廓位置信息，然后由測得數據計算得出圓度誤差。但是，對于在線圓度評定而言，應該考慮到磨削加工過程中，工件輪廓尺寸在被測量的同時也在被砂輪磨削，即工件輪廓尺寸也在不斷變化。工件磨削加工過程時工件橫截面示意圖，如圖5所示。

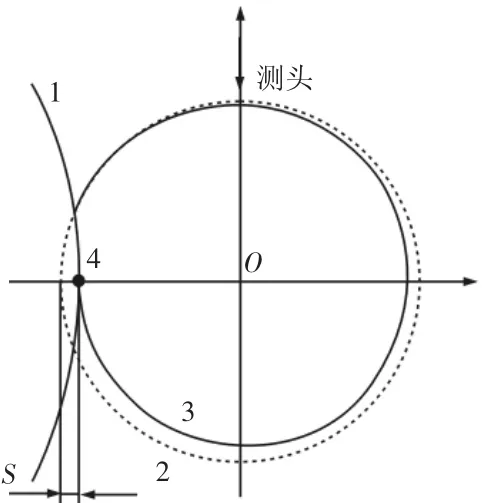
圖5 磨削過程工件橫截面示意圖Fig.5 Schematic Diagram of Cross Section of Workpiece in Grinding Process

圖中：曲線1—砂輪輪廓線；虛線2—砂輪不進給時工件理想截面；

實線3—砂輪進給時工件理想截面；點4—砂輪輪廓在砂輪

進給方向上點；S—工件旋轉一周時砂輪進給量；O—工件旋

轉軸心；測頭固定在工件正上方（可任意位置）。

磨削加工進行時，工件以一定轉速轉動的同時砂輪持續進給，假設砂輪進給速度不變，點4可認為是砂輪磨削工件的磨削點，工件磨削過程中實際輪廓3是工件旋轉是被磨削形成的，即線3由點4構成。點4勻速接近工件旋轉軸心O，并且工件勻速轉動。在幾何學知識中，一個點勻速離開（靠近）一個固定點的同時又以固定的角速度繞該固定點轉動而產生的軌跡稱為阿基米德螺線（等速螺線），其極坐標方程式為：r=a+bθ（a，b∈R）

通過對磨削過程中工件實際輪廓形成的分析，可以做出如下假設：工件勻速轉動，砂輪勻速進給時，不考慮工件旋轉偏心、機床振動、砂輪震顫等其他因素，在理想條件下，磨削過程中的工件表面輪廓橫截面是阿基米德螺線。磨削加工過程中的在線圓度評定實際就是對近似于阿基米德螺線的螺旋線的圓度評定。

在線圓度誤差評定相對于機后圓度誤差評定而言，工件實際輪廓半徑變化不僅僅來源于圓度誤差本身，還包括砂輪進給所造成的尺寸變化。而在磨削加工中，磨削到尺寸前往往有光磨階段，用以修整和降低工件圓度誤差。在光磨時可以消除砂輪進給時所造成的尺寸變化，即理想情況下，將工件輪廓截面的“阿基米德螺線”修整為圓。

在線圓度評定技術的原理就是由得到的磨削進程中的實際輪廓測點半徑值，先通過尺寸補償將“阿基米德螺線”補償為“圓”，然后求“圓”的圓度誤差，其原理如下：

（1）設工件實際輪廓表面測得極坐標為（Ri，θi），（i=1，2，…，m），其中Ri是測點的極徑，θi是測點的極角。對Ri其進行尺寸補償，設直線l為以θi為橫坐標，以Ri為縱坐標的直角坐標系中測點的最小二乘擬合線，斜率為k為補償后的極徑值，則

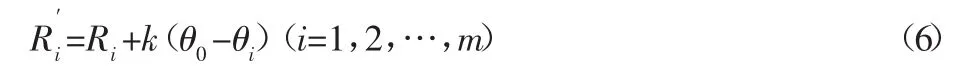
2.3 機后與在線圓度評定對比

為分析研究在線圓度評定理論的合理性、正確性，將在線圓度評定與機后圓度評定做對比分析。為方便分析起見，不妨假設最小二乘圓圓心與工件旋轉軸心重合，如圖5所示。橫坐標為工件圓周測點極角，縱坐標為測點極徑。機后圓度評定，其中實線la縱坐標值為最小二乘圓半徑R，實線la可以視為由最小二乘圓上的點構成，顯然也是所有測點最小二乘直線，如圖6所示。兩虛線為平行于實線la，包容所有測點且直線間距離最短的兩條線，則其圓度誤差評定值即為兩虛線間距離。主動測量在線圓度評定，其中實線lb為所有測點的最小二乘直線，如圖7所示。兩虛線為平行于實線lb，包容所有測點且直線間距離最短的兩條線，同理其圓度誤差評定值即為兩虛線間距離。θ為最小二乘直線與橫坐標夾角，設加工過程中，某時刻工件半徑平均值為r，工件旋轉一周時砂輪進給量為 s，則

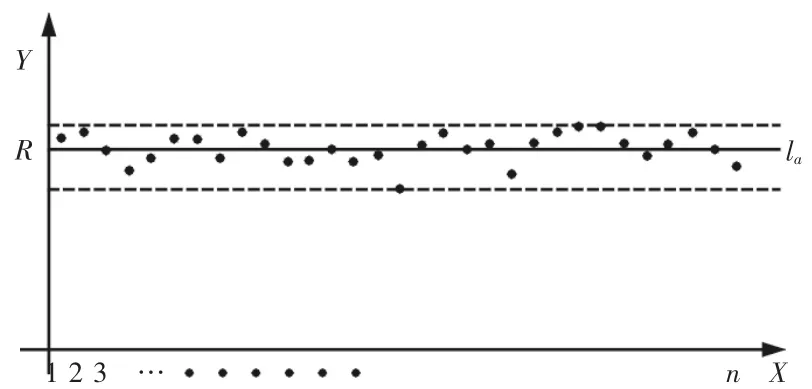
圖6 機后圓度評定Fig.6 After Machining Roundness Evaluation

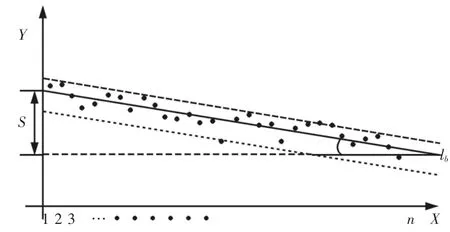
圖7 主動測量在線圓度評定Fig.7 On Line Measurement of Active Measurement

lb斜率不為0，這是因為在線圓度評定時砂輪在實時進給，工件實際輪廓半徑值不斷變化造成的。在線圓度評定中的尺寸補償就是將補償lb使其等價于la，將在線圓度評定變為機后圓度評定，進而求得圓度誤差值。同時，對比分析可知在線圓度評定和機后圓度評定一樣，理論方法符合最小二乘原理，評定原則滿足最小二乘評定準則。

3 實驗

實驗機床采用MGB1320E高精度半自動外圓磨床，如圖8所示。磨削工件材料為45鋼，磨削外圓直徑為24mm，外圓軸向尺寸為30mm；砂輪材質為棕剛玉，直徑400mm，厚度32mm，最高線速度35m/s；磨削液使用濃度為4%的乳化液；磨削方式為外圓切入磨削。實驗安排：砂輪以一定磨削切入速度進給一定加工余量后光磨至到尺寸，其中磨削切入速度、磨削加工余量和光磨余量分別設定兩個水平變量，如表1所示。實驗安排共計23=8組。

圖8 磨削實驗設備Fig.8 Grinding Experiment Equipment

表1 工藝參數水平表Tab.1 Level of Process Parameters

磨削過程中，使用磨加工主動測量儀分別由在線圓度評定模塊和機后圓度評定模塊測定磨削切入進給時的圓度誤差。磨削完成后，機后圓度評定模塊檢測工件最終的實際圓度誤差。最終實驗結果數據為在線模塊下磨削進程時圓度值A（μm）、機后模塊下磨削進程時誤差值B（μm）、磨削完成時工件實際圓度值C（μm），計算分析數據D為A相對于C的誤差、E為B與A的差值（μm），同時工件旋轉速度為300r/min，可計算得出工件旋轉一周時砂輪進給量F（μm）、G為E相對于F的誤差結果，如表2所示。由表2可以看出，在線圓度評定得到的圓度誤差值與磨削完成后實際圓度誤差值的差值絕對值最大不超過10%，證明了在線圓度評定理論的可行性；同時，常見的機后圓度評定在磨削進程時得到的圓度評定值B與在線圓度評定值A的差值E，與砂輪在工件旋轉一周時的進給量F的差值絕對值不超過18%，證明了機后圓度誤差評定與在線圓度評定得到的圓度誤差值的差主要來源于工件旋轉是砂輪的進給，間接證明了在線圓度評定尺寸補償理論的正確性。

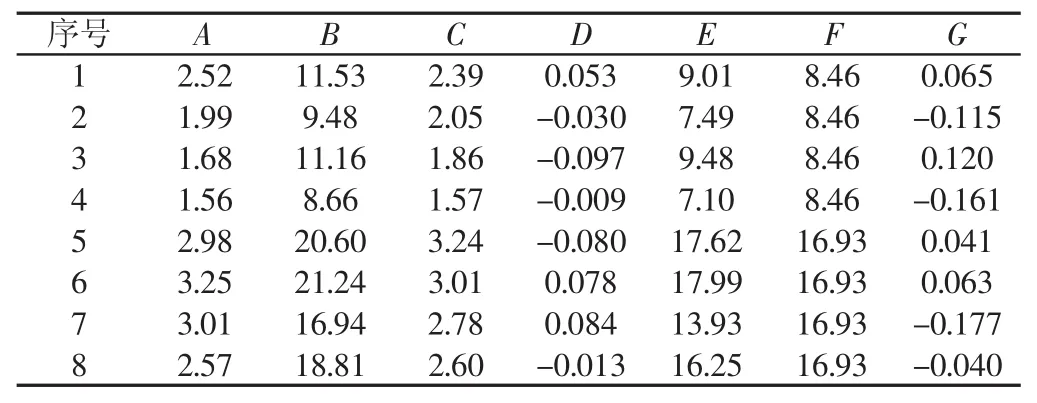
表2 實驗及分析結果Tab.2 Experimental and Analytical Results

4 結論

研究了高精密磨削加工中磨加工主動測量儀對工件尺寸和表面圓度同時檢測時的工作流程；通過對磨削進程時工件實際表面輪廓橫截面形成的分析，得出在理想條件下，工件在磨削加工時表面輪廓截面為阿基米德螺線。結合最小二乘法原理和評定準則，提出了一種尺寸補償法的在線圓度評定技術。通過實驗證明：在線圓度評定得到的圓度誤差值與磨削完成時工件實際圓度誤差值的差值絕對值最大不超過10%，驗證了在線圓度評定理論的可行性；機后圓度誤差評定與在線圓度評定得到的圓度誤差值的差值與工件旋轉一周時砂輪進給量的差值絕對值最大不超過18%，證明了機后圓度誤差評定與在線圓度評定得到的圓度誤差值的差主要來源于工件旋轉是砂輪的進給，間接證明了在線圓度評定理論尺寸補償的正確性。該研究對于實現磨加工主動量儀在線圓度評定具有重要意義。

［1］劉逸飛，鄒雪妹，談理.基于誤差分離技術的圓度自動檢測的研究［J］.機械設計與制造，2013（2）：147-149.（Liu Yi-fei，Zou Xue-mei，Tan Li.Research of roundness auto detection based on error separation technique［J］.Machinery Design&Manufacture，2013，（2）：147-149.）

［2］張珂，鄭朝方，吳玉厚.PMAC-PC下零件圓度誤差的在線測量［J］.沈陽建筑大學學報：自然科學版，2005（5）.（Zhang Ke，Zheng Chou-fang，Wu Yu-hou.On line measurement of roundness error of parts nnder PMAC-PC［J］.Journal of Shenyang Construction University：Natural Science Edition，2005（5）.）

［3］張玉梅，左春檉，李春芳.基于IRM和小波變換的圓度誤差在線檢測技術［J］.農業機械學報，2009，（7）：212-216.（Zhang Yu-mei，Zuo Chun-cheng，Li Chun-fang.Roundness on-machine measurement method based on IRM and wavelet transform［J］.Transactions of the Chinese Society for Agricultural Machinery，2009（7）：212-216.）

［4］史少杰.基于LabVIEW的新型在線圓度測量裝置的研究［D］.洛陽：河南科技大學，2015：1-5.（Shi Shao-jie.New on-line roundness measuring device based on lab-VIEW［D］.Luoyang：Henan University of Science and Technology，2015：1-5.）

［5］高方.磨加工主動測量控制的關鍵技術及應用［D］.鄭州：鄭州大學，2014：46-48.（Gao Fang.The application of the key technology of grinding active measurement control［D］.Zhengzhou：Zhengzhou University，2014：46-47.）

［6］王雪.基于切比雪夫逼近理論的形狀誤差評定算法研究［D］.北京：北京工業大學，2012：1-3.（Wang Xue.Algorithm for form error evaluation based on chebyshev approximation theory［D］.Beijing：Beijing University of Technology，2012：1-3.）

［7］方沁林.圓度誤差評定的算法研究與軟件設計［D］.武漢：華中科技大學，2007：6-7.（Fang Qin-lin.Research on roundness evaluation algorithm and programming［D］.Wuhan：Huazhong University of Science and Technology，2007：6-7.）

［8］黃長藝.機械工程測量與測試技術［M］.北京：機械工業出版社，2004.（Huang Chang-yi.Mechanical Engineering Measurement and Testing Technology［M］.Beijing：China Machine Press，2004.）

［9］李紅.數值分析［M］.武漢：華中科技大學出版社，2003：63-72.（Li Hong.Numerical Analysis［M］.Wuhan：Huazhong University of Science and Technology Press，2003：63-72.）

［10］岳奎.最小二乘圓法評定圓度誤差的程序設計［J］.工具技術，2006，（4）：79-81.（Yue Kui.Programming for evaluation of roundess error by least squares mean circle method［J］.Tool Technology，2006（4）：79-81.）