轉差對雙饋風機短路電流工頻分量的影響分析

付元歡 何 璇

（1.廣東電網有限責任公司電力調度控制中心，廣東廣州510600；2.廣東電網發展研究院有限責任公司，廣東廣州510080）

0 引言

隨著并網風電數量的增加，作為風電場主流機型的雙饋風力發電機（DFIG）[1]對短路電流的影響越來越不容忽視。文獻[2]將DFIG與鼠籠異步電機進行類比求解了三相短路電流，文獻[3]提出了求解短路電流的簡化線性模型，文獻[4]將含DFIG的分布式電源統一等效為受控電流源，文獻[5]則考慮了Crowbar電阻對短路電流的影響，但上述研究都未涉及轉差這一工況對短路電流工頻分量的影響。

本文利用DFIG的數學模型和電網故障下短路電流的表達式，分析了轉差較大和較小時DFIG工頻分量的構成；并通過Matlab/Simulink仿真驗證了本文分析結論的正確性。

1 DFIG數學模型

忽略磁飽和現象，定、轉子均采用電動機慣例，DFIG在定子三相靜止坐標系下電壓和磁鏈的標幺值空間矢量方程為[2]：

式中，vs、is、Ψs分別為定子電壓、電流和磁鏈矢量；vr、ir、Ψr分別為歸算至定子側轉子電壓、電流和磁鏈矢量；ωr為轉子角速度；Lm為勵磁電感；Rs、Ls（=Lm+Lsσ）、Lsσ分別為定子電阻、電感和漏電感；Rr、Lr（=Lm+Lrσ）、Lrσ分別為轉子電阻、電感和漏電感。

2 DFIG短路電流分析

設t=0時電網發生短路故障，Crowbar電路投入，DFIG端口電壓跌落深度為Kd。聯立式（1）、（2）可得DFIG短路電流的表達式為[5]：

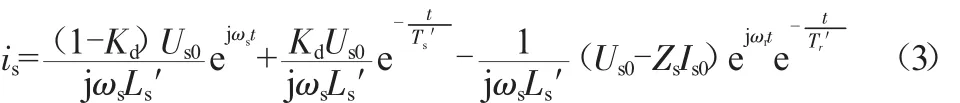
式中，Us0、Ls0為短路前定子電壓、電流；Zs（=Rcb+jωsLs′）為定子側等效阻抗；Rcb為撬棒電阻阻值；ωs為工頻角速度；Ls′=Ls-Lm2/Ls為定子暫態電感；Ts′=Ls′/Rs為定子暫態時間常數；Tr′=Lr′/（Rr+Rcb）為轉子暫態時間常數。

DFIG的短路電流與傳統同步發電機的短路電流不同，除了有穩態工頻分量和直流衰減分量外，還存在與轉子角速度有關的轉子頻率衰減分量。因此，當轉子角速度大小不同時，轉子頻率分量可能是工頻分量也可能是非工頻分量。

2.1 轉差較大時工頻分量

在傳統的電力系統分析中，一般將轉差在±2%～±5%的普通異步電機當作同步電機進行處理[6]。因此，當轉差在±5%以外時，轉子頻率分量可視作非工頻分量進行處理，即認為轉子頻率分量能被濾波器濾除。此時短路電流中工頻分量的大小為：

短路電流的工頻分量大小與時間無關，與端口電壓大小、端口電壓跌落程度和定子暫態電抗有關。

2.2 轉差較小時工頻分量

當轉差在±5%以內時，轉子頻率與工頻無異，轉子頻率分量可視作工頻分量。此時短路電流中工頻分量的大小為：

短路電流工頻分量的大小隨著電網故障發生后的時間而變化，呈現出一個指數衰減過程。在短路發生瞬間工頻分量最大。

3 仿真驗證

在Matlab/Simulink中搭建如圖1所示的9 MW的風電場模型進行仿真驗證。該風電場由6臺1.5 MW的風機組成，經過母聯、升壓變壓器和傳輸線后并入無窮大電網當中。通過在母聯出線端口處設置三相短路故障，來驗證本文對短路電流工頻分量的分析結論。

圖19 MW風電場結構拓撲圖

表1展示了轉差較大時（｜s｜＞0.05）三相短路電流工頻分量大小，其中三相短路故障帶有0.1 p.u.的過渡電阻。從表中可以看出，公式與仿真結果十分吻合，誤差都不超過1%。表明轉差較大時公式（4）能精確計算短路電流工頻分量。

表2展示了轉差較小時（｜s｜≤0.05）三相短路電流工頻分量大小，其中三相短路故障帶有不同大小的過渡電阻。從表中可以看到，公式與仿真結果誤差不超過5%，在誤差允許范圍內。表明轉差較小時公式（5）能精確計算短路電流工頻分量。

表2 短路瞬間工頻分量大小（轉差s=0）

4 結語

本文利用DFIG的數學模型和電網故障下短路電流的表達式，分析了轉差較大和較小時DFIG工頻分量的組成。轉差較大時DFIG短路電流轉子頻率分量不用被計及；轉差較小時轉子頻率分量相當于工頻分量，應當被計及。仿真結果驗證了本文分析結論的正確性。

[1]年珩，程鵬，賀益康.故障電網下雙饋風電系統運行技術研究綜述[J].中國電機工程學報，2015，35（16）：4184-4197.

[2]MORREN J,DE HAAN S W H.Short-Circuit Current of Wind Turbines With Doubly Fed Induction Generator[J].IEEE Transactions on Energy Conversion,2007,22(1):174-180.

[3]周宏林，楊耕.不同電壓跌落深度下基于撬棒保護的雙饋式風機短路電流特性分析[J].中國電機工程學報，2009，29（S1）：184-191.

[4]肖繁，張哲，尹項根，等.含雙饋風電機組的電力系統故障計算方法研究[J].電工技術學報，2016，31（1）：14-23.

[5]潘文霞，楊剛，劉明洋，等.考慮Crowbar電阻的雙饋電機短路電流計算[J].中國電機工程學報，2016，36（13）：3629-3634.

[6]何仰贊，溫增銀.電力系統分析[M].武漢：華中科技大學出版社，2002.