脈沖清灰系統噴嘴型面結構參數優化

趙安文，郭 聳，高 尚

（南京理工大學化工學院，江蘇南京210094）

隨著現代工業生產技術的不斷發展，以煙塵、粉塵等細微顆粒物為主的粉塵污染廣泛存在于電力、垃圾焚燒、噴涂、水泥、化工、重金屬礦等行業[1-2]。由于粉塵粒徑十分微小，難以捕捉，化工生產中通常采用以脈沖噴吹清灰方式為主的除塵設備來過濾和凈化作業場所環境氣體[3-5]，以降低空氣中粉塵、煙塵顆粒的含量。噴吹管作為脈沖噴吹除塵設備的核心部件，其結構參數的改變將直接影響除塵設備的清灰效果[6-7]。

目前關于脈沖噴吹管結構參數對除塵設備清灰效果的影響，國內外學者已在模型實驗和數值模擬兩方面進行了大量的研究工作。模型試驗測量方面，Lo等[8-9]和Yan等[10]采用不同開孔直徑脈沖噴吹管，結合脈沖噴吹清灰機理，對濾袋內部及其表面壓力場的分布規律進行了研究，結果表明：影響脈沖清灰效果的一個重要因素是噴吹管口氣流脈沖壓力，氣流壓力越大，粉塵受到的分離力越大，清灰效果越好。數值模擬方面，張景霞等[11]和樊百林等[12]針對脈沖噴吹管各出口氣流流量分布不均勻現象，提出了一套基于流量修正的管口孔徑迭代計算公式，有效地改善了噴吹管各出口氣流流量分布不均勻現象。隨后Li等[13]和Chen等[14]基于流量修正的噴嘴孔徑設計方法，分析研究不同開孔形狀以及不同開孔個數條件下噴吹管出口壓力大小，發現矩形噴嘴出口總壓值較小，適用于噴吹短濾袋，而圓形文丘里噴嘴出口總壓值較大，適用于噴吹中等長度濾袋。

學者已從多方面探討了噴吹管結構參數（噴嘴開孔直徑、噴嘴間距、噴吹管長度等）的變化，對噴嘴出口氣流壓力大小以及氣流流量分布均勻性的影響，而關于噴嘴出口截面氣流參數分布均勻性的研究內容卻未見報道。工程實際應用發現，除塵設備使用一段時間后，濾袋局部小面積損壞現象時有發生[15-16]，因此，基于前人的研究基礎，推測該現象的發生正是由于噴嘴出口截面各項氣流參數分布不均勻造成。改變噴嘴與噴吹管連接部位型面參數，對比分析噴嘴出口截面各項氣流參數的分布差異性，評估氣流機械能損失率，在優化噴嘴出口流場品質、延長濾袋使用壽命以及降低系統能耗等方面將具有重要影響意義。

1 噴嘴結構參數設計

1.1 確定噴嘴結構參數

數值模擬實驗研究目的在于改變噴嘴與噴吹管連接部位間的型面結構參數以及對比分析不同型面噴嘴出口截面氣流參數分布規律的差異性，故研究時可建立只包含單一噴嘴結構的噴吹管模型。根據噴嘴壁面與噴吹管壁面在連接部位的幾何位置關系，將噴嘴型面結構分為4類（假設兩者壁面間的夾角為α），分別為擴張型（0°＜α＜90°）、直角型（α=90°）、收縮型（90°＜α＜180°）和圓角型（連接部位型面以倒圓角方式光滑過渡）。考慮到氣體介質在噴吹管以及噴嘴內部的運動情況為等熵流動，對于收縮型和擴張型噴嘴結構，為避免收縮（擴張）過于劇烈而導致氣體與壁面分離，故收縮（擴張）角的取值大小在3～5°范圍內為宜[17]。相似地，噴嘴與噴吹管連接部位型面倒圓半徑同樣不宜過大。最終所有噴嘴模型的具體結構參數如表1所示，w表示噴吹管直徑，D表示噴嘴出口截面直徑，H表示噴嘴長度，α表示噴嘴壁面與噴吹管連接壁面間的夾角，R表示噴嘴壁面與噴吹管連接壁面間的倒圓半徑。

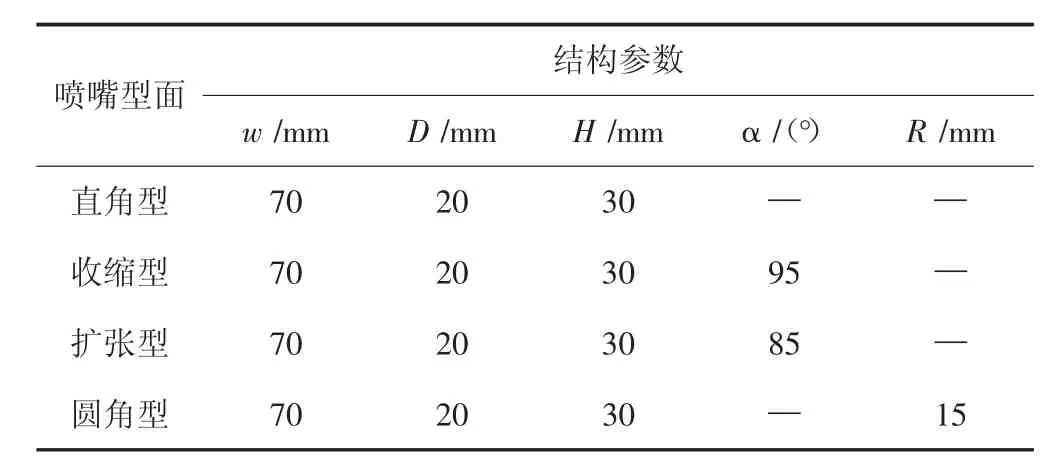
表1 不同噴嘴型面結構參數Tab.1 Different nozzle profile parameters

1.2 幾何建模與網格劃分

采用專業制圖軟件CAD建立噴吹管二維數值計算模型，圖1為4種噴嘴型面結構示意。L1表示噴嘴與噴吹管入口位置間距，L2表示噴嘴與噴吹管末端壁面間距。

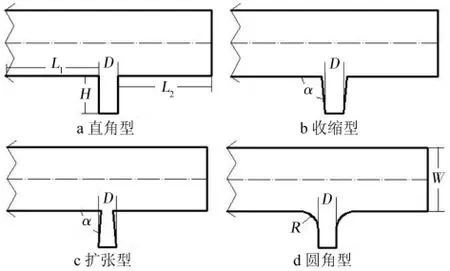
圖1 噴嘴型面結構示意Fig.1 Scheme of nozzle profile structure

模型建立完成后，采用四邊形主導網格劃分方法對模型進行網格劃分，根據黏性流體的流動特征，網格劃分時對噴吹管和噴嘴的近壁面區域流場網格進行加密處理，保證第1層網格單元位于層流底層（黏性子層）中。在計算過程中還對噴嘴主流場區域內的網格進行了自適應劃分處理，目的在于提高計算結果精度，確保數值計算結果與模型網格數量保持獨立。

1.3 數學模型與邊界條件

由于噴吹管內氣體流動的定常結算結果與非定常計算結果之間的誤差非常微小[18]，考慮到計算成本，數值模擬試驗將忽略各計算參數在時間坐標系下的離散化處理，采用基于壓力-速度修正的耦合求解器，并設置為定常（穩態）計算。操作環境壓力設置為一個標準大氣壓，氣體湍流運動控制方程采用κ-ε標準湍流模型[5，11-12]，選用空氣作為噴吹管內部流動氣體材料。由于氣體流動馬赫數超過0.3時，須考慮氣體壓縮效應對流場參數分布產生的影響，因此數值模擬中的氣體材料將假定為可壓縮流體，流體密度符合理想可壓縮氣體定律，計算殘差收斂精度設置為10-4（能量殘差精度為10-6）。此外，工業實際應用中通常采用空氣壓縮機為除塵設備提供壓縮氣體，故噴吹管入口采用壓力入口邊界條件：總壓為0.3 MPa，靜溫為300 K[3，5，7]；噴嘴出口設置為壓力出口邊界條件：回流壓力為-6 000 Pa[12]；所有壁面均設置為無滑移絕熱壁面。噴吹管入口位置處的湍流強度和水力學直徑[19]，根據下式確定：

式中：I為流體運動湍流強度；Re為湍流雷諾數；ρ為流體密度，kg/m3；D為管道直徑，m；υ為流體流速，m/s；μ為流體動力黏性系數，Pa·s；r為管道水力學半徑，m；Dhy為管道水力學直徑，m；A為噴吹管過流斷面面積，m2；S為噴吹管過流斷面潤濕周長，m。

2 結果分析與討論

氣體介質作黏性流動時，噴嘴近壁面流場內將會出現厚度較薄的黏性邊界層區域。由于氣流在黏性邊界層內的分布參數并不是本文中關注的重點，故所有分析計算內容將去除噴嘴壁面黏性邊界層（厚度為1 mm）內單元數據。圖2、3分別為噴嘴出口截面速度場和滯止壓力場的分布示意圖。

圖2 噴嘴出口截面速度場分布Fig.2 Velocity field distribution of nozzle outlet cross section

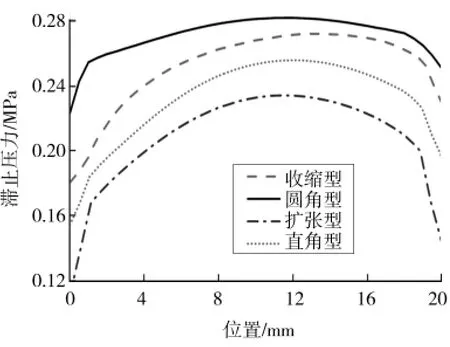
圖3 噴嘴出口截面滯止壓力場分布Fig.3 Pressure field distribution of nozzle outlet cross section

從圖2、3中可以看出，收縮型、直角型、擴張型和圓角型噴嘴出口截面速度場的分布性均較為理想。相似地，忽略近壁面邊界層區域，所有噴嘴出口截面滯止壓力場的分布均呈光滑拋物型，相比之下圓角型噴嘴出口截面滯止壓力參數的變化幅度最小。

標準偏差值能夠較好地反映樣本數據的變化幅度，因此噴嘴出口截面各項氣流參數的分布均勻性將依據所有網格單元數據標準偏差值來評判。噴吹管入口邊界條件保持相同時，表2所示為各噴嘴出口截面氣流參數標準偏差對比。

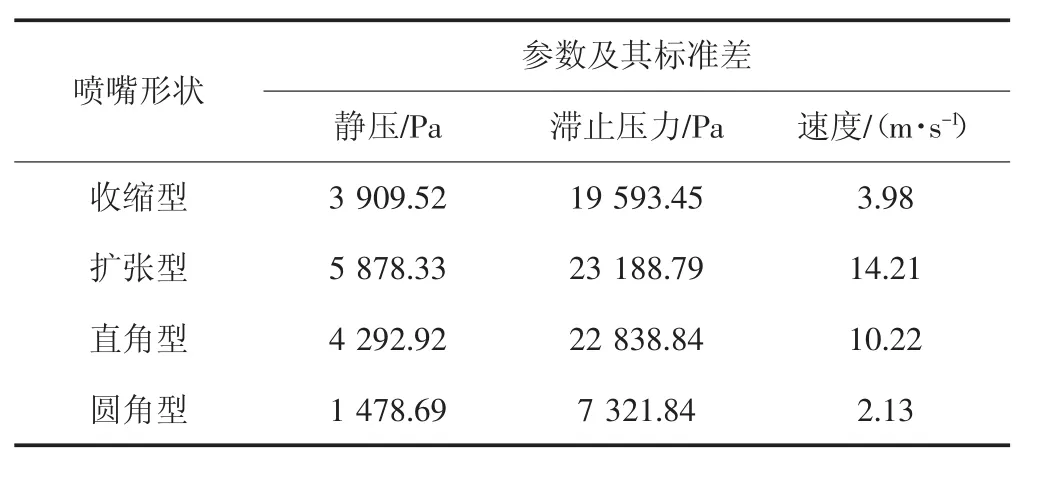
表2 氣流參數標準差分析Tab.2 Standard deviation analysis of airflow parameters

由表可知，圓角型噴嘴出口截面速度參數的標準偏差值最小，分別為收縮型、擴張型和直角型噴嘴對應參數的53.52%、14.99%、20.84%，表明圓角型噴嘴出口截面速度場的分布均勻性最優。

圓角型噴嘴出口截面靜壓參數的標準偏差值也最小，分別為收縮型、擴張型和直角型噴嘴對應參數的37.82%、25.15%、34.44%；相似地，圓角型噴嘴出口截面滯止壓力參數的標準偏差值分別為收縮型、擴張型和直角型噴嘴對應參數的37.37%、31.58%、32.06%，表明圓角型噴嘴出口截面滯止壓力場的分布均勻性最優。故可說明噴嘴與噴吹管壁面連接部位型面采用倒圓設計，噴嘴出口截面各項氣流參數的分布均勻性最優，流場品質最高，從而可有效避免濾袋局部小面積損壞現象的發生，延長濾袋的使用壽命。

已有研究結果表明[20]，脈沖壓力（滯止壓力）大小是評判除塵設備清灰效果的重要指標。噴嘴出口截面滯止壓力數值越大，表明系統清灰效果越好。圖4為不同型面噴嘴出口截面平均滯止壓力對比示意圖。

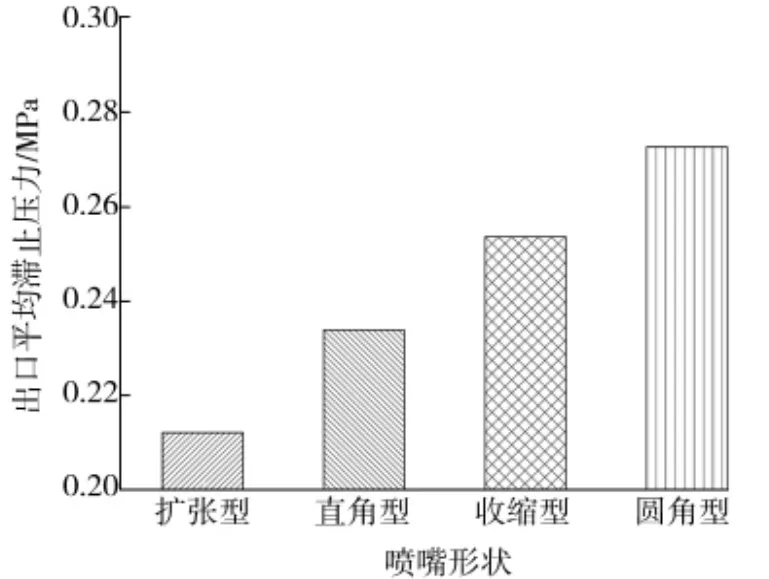
圖4 4種型面噴嘴出口截面平均滯止壓力對比Fig.4 Comparison of average stagnation pressure for outlet cross section of four kinds of nozzles

從圖中可以看出，噴吹管入口邊界條件保持相同時，噴嘴出口截面平均滯止壓力的大小關系為：擴張型＜直角型＜收縮型＜圓角型。以目前工業實際常用直角型噴嘴平均滯止壓力參數值為基準，收縮型、擴張型和圓角型噴嘴出口截面平均滯止壓力值分別為直角型噴嘴的1.09、0.91和1.17倍。

圖5為4種型面噴嘴內流場速度矢量分布示意圖。

圖5 4種型面噴嘴內流場速度矢量圖Fig.5 Flow field velocity vector of four kinds of nozzles

從圖中可以看出，在收縮型、擴張型和直角型噴嘴與噴吹管連接部型面流場內存在不同尺寸大小的渦旋區域，故氣流在此區域內將會產生較大的能量損失。

為進一步分析相同入口參數條件下，4種噴嘴出口位置氣流機械能損失量間的關系，采用如下公式計算氣流經過噴嘴后的平均滯止壓力損失率。

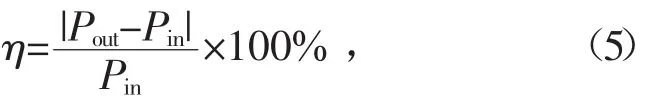
式中：η為氣流平均滯止壓力損失率；Pout為噴嘴出口截面平均滯止壓力，Pa；Pin為噴吹管入口截面平均滯止壓力，Pa。

根據公式計算得到氣流經過擴張型、直角型、收縮型和圓角型噴嘴后，平均滯止壓力的損失率分別為29.28%，22.03%，15.44%，9.10%，表明噴嘴與噴吹管壁面連接部位采用倒圓設計不僅能夠增大噴嘴出口截面平均滯止壓力，還可減少氣流機械能損失量，降低系統能耗。

3 型面參數優化

噴嘴與噴吹管連接部位型面采用倒圓型設計不僅能夠減少內部流體介質的機械能損失，還能提高噴嘴出口截面各項氣流參數分布的均勻性，優化流場品質，因此有必要針對不同開孔直徑的圓角型噴嘴，研究倒角半徑的變化對其出口流場品質的影響。

3.1 實驗設計

采用控制變量法進行實驗設計，只考慮噴嘴直徑與噴吹管連接部位曲面倒圓半徑對其出口截面各項氣流參數分布規律的影響。噴嘴直徑和倒圓半徑2個目標變量均以等差數列的形式線性變化，并且試驗進行時能保證2個目標變量的取值相互正交，共計開展25組實驗。

3.2 計算結果分析與討論

由于均方根法能夠更靈敏地反應樣本數據的分布均勻性，故構造如下形式的參數均方根計算公式：

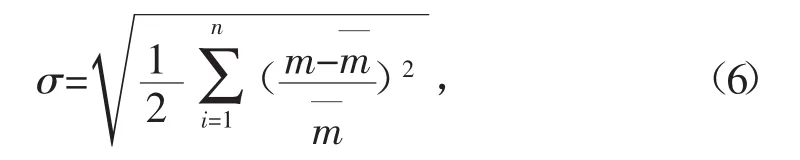
式中：σ為某一氣流參數分布均勻性的均方根值；n為噴嘴出口截面數據存儲（網格）單元數；m為每個數據存儲單元中對應氣流參數的數值；m為截面所有數據存儲單元中對應氣流參數的平均值。

根據各組數值模擬結果計算噴嘴出口截面對應氣流參數（靜壓、滯止壓力和速度參數）的均方根值。表3為每組實驗對應氣流參數均方根計算值，表中σsp、σtp、σvel分別表示噴嘴出口截面靜壓、滯止壓力和速度參數的均方根值。

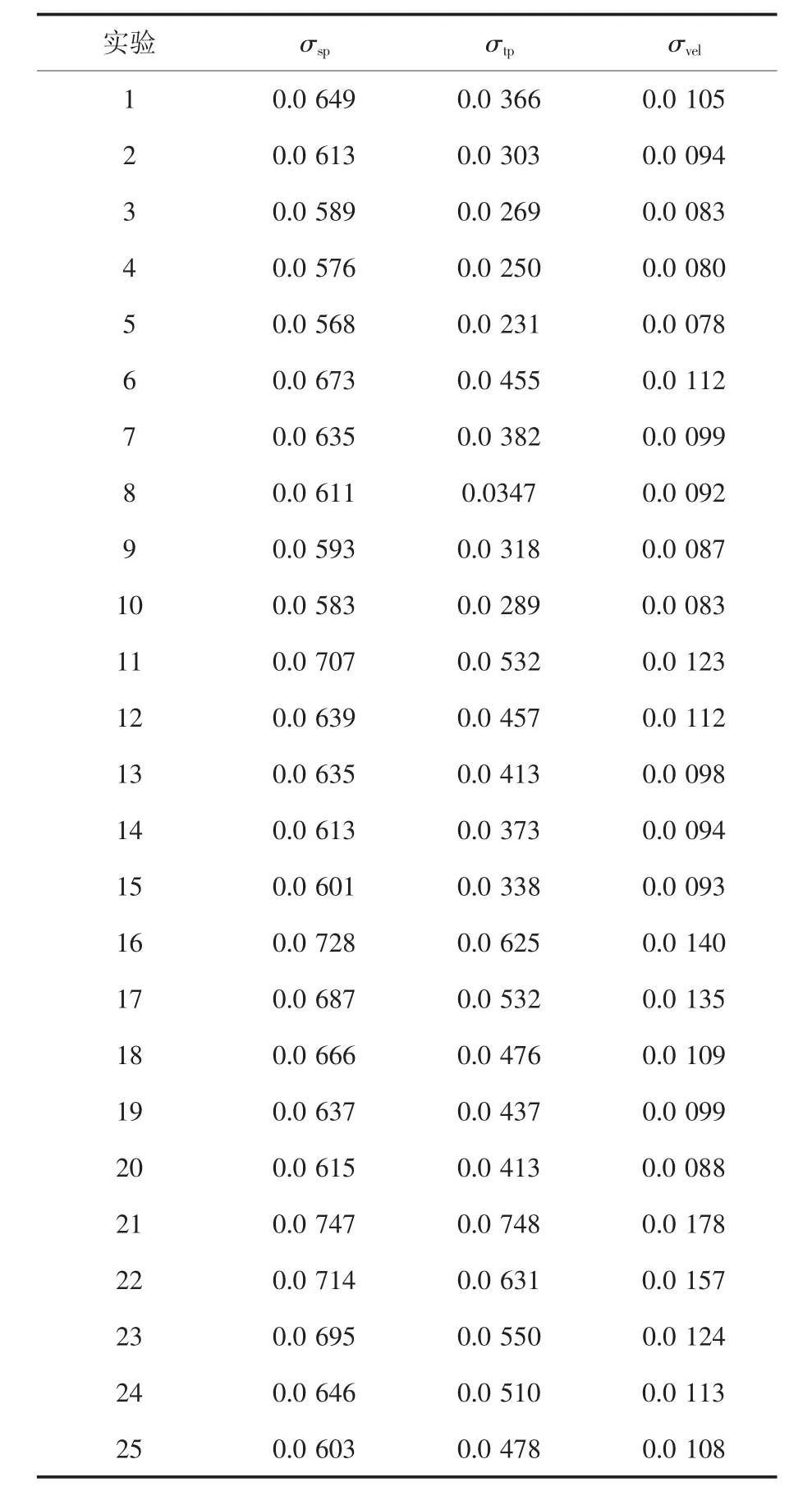
表3 氣流參數均方根計算值Tab.3 Square root of airflow parameters

從表中數據可以看出，同一氣流參數在各組實驗中的計算值各不相同，表明噴嘴直徑和連接曲面倒圓半徑2個結構參數的變化將對噴嘴出口流場各項氣流參數的分布均勻性產生影響。

為更加直觀地分析噴嘴結構參數與出口流場氣流參數分布均勻性間的影響關系，以滯止壓力參數的均方根值為例進行分析討論。圖6為曲面倒圓半徑與滯止壓力均方根值間的關系示意圖。

圖6 倒圓半徑與滯止壓力均方根值間的關系示意Fig.6 Variation trend between fillet radius and square root of stagnation pressure

從圖中可以看出，噴嘴直徑保持相同，隨著曲面倒圓半徑的增大，滯止壓力參數的均方根值在逐漸減小；表明增大曲面倒圓半徑，有利于提高噴嘴出口流場滯止壓力參數的分布均勻性。

圖7為噴嘴直徑與滯止壓力均方根間的關系示意圖。

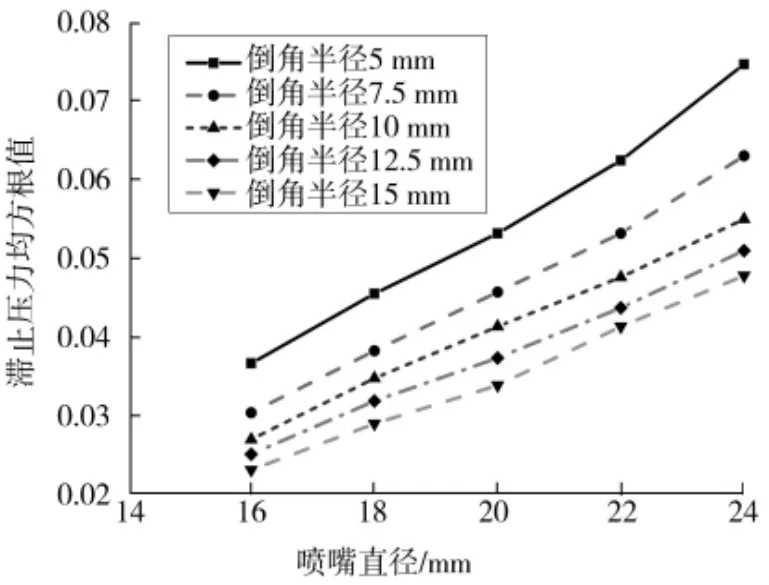
圖7 噴嘴直徑與滯止壓力均方根值間的關系示意Fig.7 Variation trend between nozzle diameter and square root of stagnation pressure

從圖中可以看出，曲面倒圓半徑保持相同，隨著噴嘴直徑的增大，滯止壓力參數的均方根值在逐漸增大；表明增大噴嘴直徑，將降低其出口流場滯止壓力參數的分布均勻性。

相似地，噴嘴直徑保持相同，隨著曲面倒圓半徑的增大，靜壓和速度參數的均方根值均逐漸減小；曲面倒圓半徑保持相同，隨著噴嘴直徑的增加，靜壓和速度參數的均方根值均逐漸增大。表明增大噴嘴與噴吹管連接部位曲面倒圓半徑，以及減小噴嘴開孔直徑，有利于提高噴嘴出口各項氣流參數的分布均勻性，改善流場品質。

4 結論

通過改變噴嘴與噴吹管連接部位型面結構參數，分析討論噴嘴出口截面各項氣流參數分布均勻性的變化，可得如下結論。

1）保持噴吹管入口邊界條件相同，擴張型、直角型、收縮型和圓角型噴嘴出口截面氣流滯止壓力的損失率分別為29.28%、22.03%、15.44%、9.10%，表明噴嘴與噴吹管連接部位型面采用圓角型設計可減少氣流機械能損失，降低系統能耗。

2）保持噴吹管入口邊界條件相同，圓角型噴嘴出口截面滯止壓力、靜壓和速度參數的標準偏差值均最小，表明噴嘴與噴吹管連接部位型面采用圓角型設計能夠提高噴嘴出口流場各項氣流參數的分布均勻性。

3）增大噴嘴與噴吹管連接部位曲面倒圓半徑，以及減小噴嘴開孔直徑，有利于提高噴嘴出口各項氣流參數的分布均勻性，改善流場品質。

（

）：

[1]FAN B L，WANG H W，HUANG G H.Interaction of local members in dust removal system[C]//USA:2014 International Academic Conference on the Environment，Energy and Power Engineering，2014:570-574.

[2]易玉枚，李顯杰，廖可兵，等.濾料脈沖噴吹清灰效果評價指標的試驗研究[J].中國安全科學學報，2014，24（7）:135-139.

[3]萬凱迪，王智化，胡利華，等.袋式除塵器脈沖噴吹清灰過程的數值模擬[J].中國電機工程學報，2014，34（23）:3970-3976.

[4]王巖，張明星，李倩倩，等.脈沖噴吹2 000 mm長濾筒的清灰性能[J].環境工程學報，2015，9（12）:5951-5956.

[5]鐘麗萍，黨小慶，勞以諾，等.脈沖袋式除塵器噴吹管內壓縮氣流噴吹均勻性的數值模擬[J].環境工程學報，2016，10（5）:2562-2566.

[6]LI Q Q，ZHANG M X，QIAN Y L，et al.The relationship between peak pressure and residual dust of a pulse-jet cartridge filter[J].Powder Technology，2015，136（283）:302-307.

[7]呂娟，顏翠平，付瑜，等.噴吹管對濾袋清灰性能的影響[J].環境工程學報，2017，11（3）:1667-1671.

[8]LO L M，CHEN D R，DAVID Y H.Experimental study of pleated fabric cartridges in a pulse-jet cleaned dust collector[J].Powder Technology，2010，197（3）:141-149.

[9]LO L M，CHEN D R，DAVID Y H.Numerical study of pleated fabric cartridges during pulse-jet cleaning[J].Powder Technology，2010，198（1）:75-81.

[10]YAN C P，LIU G J，CHEN H Y.Effect of induced airflow on the surface static pressure of pleated fabric filter cartridges during pulse jet cleaning[J].Powder Technology，2013，249（3）:424-430.

[11]張景霞，沈恒根，方愛民，等.袋式除塵器噴吹管內氣流數值模擬分析[J].電力環境保護，2008，24（3）:30-32.

[12]樊百林，李芳芳，王宏偉，等.袋式除塵器噴吹管的氣流均勻性研究[J].中國安全生產科學技術，2015，11（8）:77-82.

[13]LI H X，CHOI H J，LI B，et al.Numerical analysis on the gas flow dynamics from a rectangular slot-nozzle for pulse cleaning of filter unit[J].Powder Technology，2016，297（8）:330-339.

[14]CHEN S W，CHEN D R.Numerical study of reverse multi-pulsing jet cleaning for pleated cartridge filters[J].Aerosol and Air Quality Research，2016，16（8）:1991-2002.

[15]KIM J U，HWANG J，CHOI H J，et al.Effective filtration area of a pleated filter bag in a pulse-jet bag house[J].Powder Technology，2017，311（15）:522-527.

[16]鄭奎照.大型電袋復合除塵器脈沖濾袋清灰[J].環境工程學報，2014，8（12）:5419-5423.

[17]易仕和.超聲速與高超聲速噴管設計[M].北京:國防工業出版社，2013.

[18]樊百林，李芳芳，王宏偉，等.基于穩態與非穩態的噴吹管內流場的對比研究[J].工業安全與環保，2016，42（9）:30-33.

[19]HOSSEINI S A，VAHEDI T H.Modeling particle-loaded single fiber efficiency and fiber drag using ANSYS-Fluent CFD code[J].Computers&Fluids，2012，66（15）:157-166.

[20]張情，陳海焱，巨敏，等.誘導噴嘴改進濾筒脈沖清灰效果的實驗研究[J].環境工程，2012，30（1）:62-65.