基于PBM和DPM的噴霧冷凍流化床液滴霧化的數值模擬

李苗苗，徐 俊，王 新，徐 慶

（天津科技大學 機械工程學院；天津市輕工與食品工程機械裝備集成設計與在線監控重點實驗室，天津300222）

液滴在固體表面的流動變化，歷來是工程領域的一個研究熱點，張建林等[1]就對液滴在固體表面的鋪展情況進行了研究。流化床包覆是指芯材在某一溫度流化氣體的流化作用下處于流化狀態，霧化的壁材與芯材接觸將芯材包埋的技術，也是微膠囊常用的制備技術[2]。包覆的壁材既可以是親水性的糖類或蛋白類，又可以是親脂性材料。Litster等[3]認為包覆的過程主要分為3個步驟：1）液滴的潤濕和成核；2）顆粒的固化和生長；3）顆粒間磨損破碎，該理論也被用來解釋流化床包覆過程。Link等[4]總結了影響包覆效果和包覆過程的影響因素，主要分為液體特性、固體特性、系統和操作變量。

在頂噴的流化床包覆過程中，主要包括氣體的流化作用、液滴的霧化作用、顆粒與液滴之間的碰撞以及液滴在顆粒表面的沉積鋪展等等。霧化液滴在流化床內隨機運動進行碰撞，碰撞過程中，如果2個表面潤濕的顆粒接觸，會形成液橋，顆粒在冷空氣的作用下，固化會導致液橋向固橋轉變，形成團聚。顆粒的團聚和破碎經歷很多微觀過程，需要引進群體平衡模型（population balance model，PBM）[5]計算顆粒的一些變量，如粒徑分布、潤濕顆粒的數量等。

PBM的模擬對象主要是多相流中副相的粒徑分布情況，如液滴、氣泡以及固態顆粒等，需要得到合適的粒徑分布規律[6-9]。計算粒徑分布主要有2種方法，一種是拉格朗日法，即離散相模型（discrete phase model，DPM），另一種是歐拉法，即PBM法。由于DPM主要模擬離散相，且僅限于稀疏相的模擬，群體平衡模型因為稀疏相均可以模擬而被廣泛提出。

本文中基于PBM和DPM，對噴霧冷凍流化床包覆過程中的霧化液滴的產生、凝固、運動進行了數值模擬，主要對霧化過程中的速度、溫度及顆粒的團聚破碎規律進行了研究。

1 數學模型

在過去的幾十年時間里，計算流體動力學（computational fluid dynamics，CFD）已被廣泛應用于噴霧領域，比如霧滴的沉積特性研究[10]、霧化效果的研究[11]等，各種數值方法，例如流體體積法、DPM已經用于預測噴嘴的霧化特性和預測液滴的軌跡[12]。DPM方法是基于拉格朗日計算方法[13]，液滴軌跡使用單獨的控制方程計算；而體積流體應用歐拉法，把各相看作是相互聯系的相計算。模擬粒子過程主要有PBM和DPM兩大體系[14]。

1.1 氣相控制方程

計算流體力學需要了解流體的動力特性，這對研究霧化過程中的流場分布有著很重要的意義，因此，為了得出流體的流速與壓力等動力學特性，在計算中，將空氣作為連續相介質處理，采用SIMPLE算法求解，方程的通用形式表示為

式中：Φ為通用變量；ΓΦ為廣義擴散系數；SΦ為廣義源相。

1.2 群體平衡模型

霧化液滴在運行的過程中會出現，聚并和破碎的行為，這在研究流化床包覆的過程中也是必須要考慮的，關于顆粒的聚并和破碎的研究，在實驗中難以控制和實現，因此本研究中引入了群體平衡模型。群體平衡模型是一組描述顆粒聚并和破碎行為的偏微分方程[15-16]，反映顆粒成長和消亡的過程。其一般表示形式為

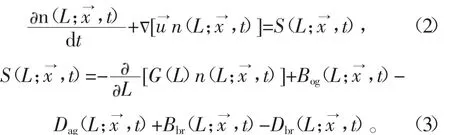
1.3 離散相模型

利用DPM可以對顆粒進行追蹤，因為它是在歐拉-拉格朗日法的基礎上建立的，所以認為液滴或顆粒是控制體內動量、質量和能量的源項。

由流化床頂部霧化器生成液滴的直徑是一組離散的尺寸，并且每種尺寸的液滴都各有其運動軌跡，沿著該軌跡的液滴的流動速度是固定的。在設定了空氣的溫度和速度后，各組尺寸液滴的控制方程就會進行迭代，計算它們的速度、軌跡、尺寸和溫度，直到這些液滴到達噴霧流化床的出口或碰撞到壁面。

追蹤顆粒軌跡是通過計算力平衡方程實現的，力平衡方程為：

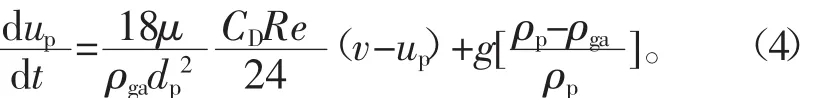
式中：v為連續相速度；up為顆粒速度；ρga為連續相密度；ρp為顆粒密度。

作用在顆粒上的力有重力、慣性力以及氣體曳力。

滑移雷諾數（Re）和曳力系數（CD）的計算公式為

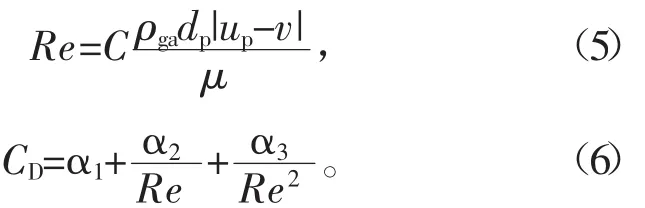
式中：dp為顆粒直徑；α1、α2、α3為顆粒球形度系數。

2 模型的建立

本幾何模型對噴霧流化床的模型[17]進行簡化，計算域如圖1所示。

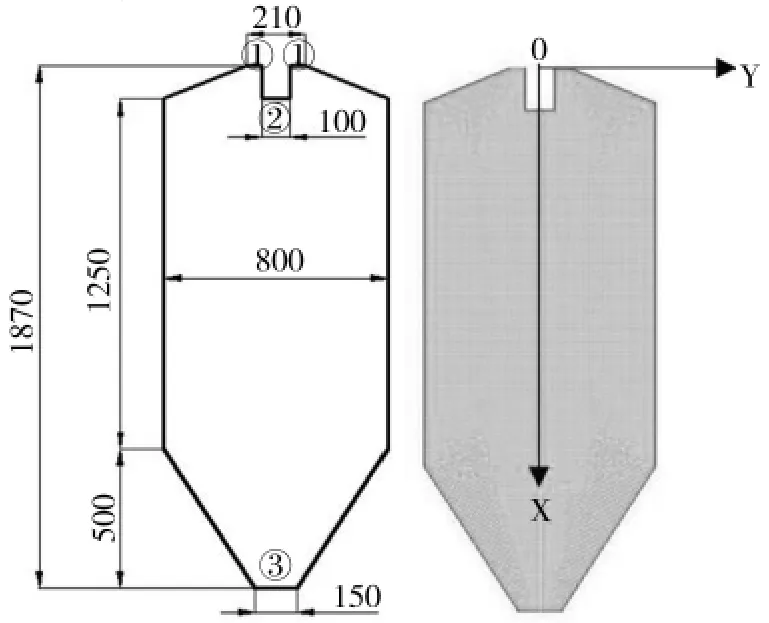
圖1 幾何模型尺寸和網格Fig.1 Size of geometric model and mesh

本研究中模型為柱錐形流化床，計算域使用二維空間進行模擬，幾何體相關尺寸參數及模型參數見表1。表中所列數據是參考了耿縣如等[17]的單液滴噴霧冷凍研究的有關數據，并進行了相關修改。

3 計算結果及討論

3.1 液滴的溫度

圖2為液滴溫度隨時間的變化圖。

表1 邊界條件和參數Tab.1 Boundary conditions and simulation parameters

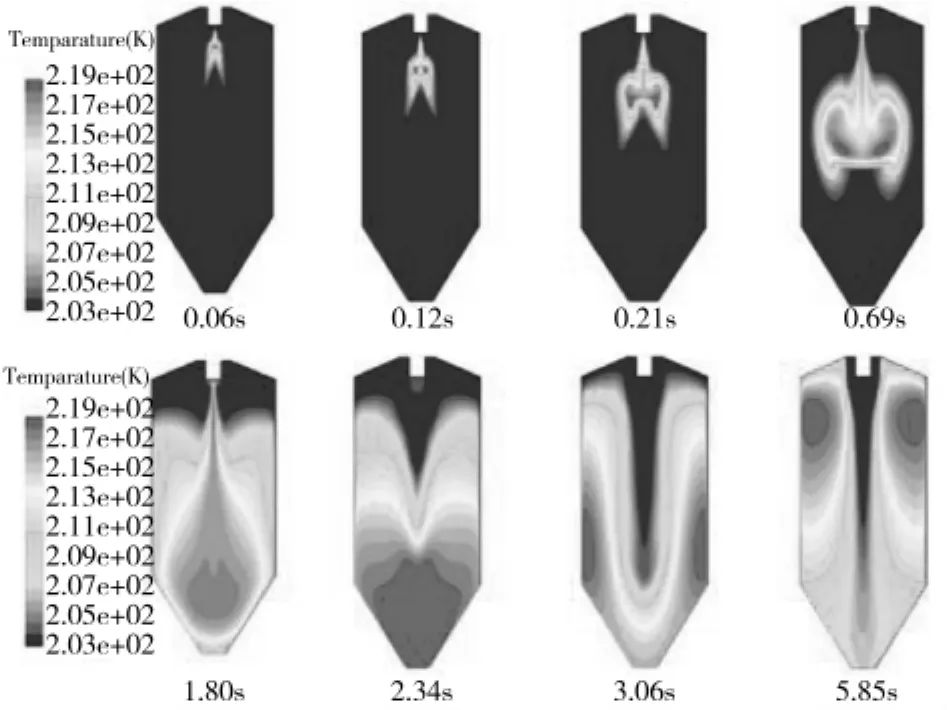
圖2 液滴溫度隨時間的變化Fig.2 Change of droplet temperature with time

由圖可知，液滴從入口噴出，在噴出時液滴溫度為300 K，由于環境溫度很低，為203 K，因此液滴在達到底部時已成凝固狀態。整個過程中，流化床內溫度在X軸兩側呈對稱分布，經過1.8 s到達錐體體部分，隨即底部溫度達到最大，繼而產生回流，之后流化床內溫度又呈對稱分布。整個過程當中，只有1.8 s到2.34 s底部溫度達到最大，到達5.85 s以后流化床內溫度在X軸兩側又呈對稱分布，這是因為霧化液滴在運動過程中，中心區域流速較大，所以會很快達到底部，而當整個過程達到穩定的過程中，霧化液滴與冷空氣接觸，溫度也逐漸下降，同時達到底部又產生回流，最終又呈現出兩邊的對稱分布。

本研究中以模型液滴入口為坐標原點，軸向為X方向，指向底部椎體部分的方向為X軸正方向。結果顯示，以X軸為軸線，兩邊成對稱分布，因此以下圖像只采取了模型的一半進行了研究。

圖3為流化床內溫度隨Y軸的變化圖。如前所述，霧化液滴的溫度會對液滴的霧化產生影響，因為液滴在溫度過低時會產生凝固現象。在流化床包覆過程中，一旦液滴涂敷在顆粒表面，是需要進行冷卻的，因此本文也研究了流化床內的溫度分布。

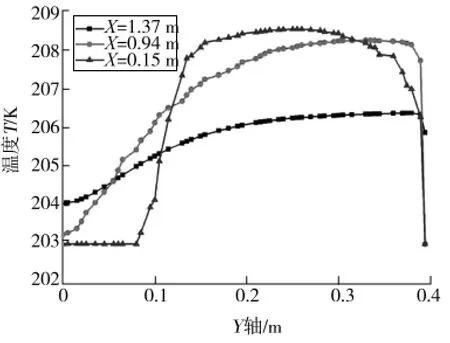
圖3 流化床內溫度隨Y軸的變化Fig.3 Temperature change with axis Y in a fluidized bed

圖3說明了霧化液滴在不同軸向位置上的溫度從Y=0 m處到壁面處的溫度變化，冷氣入口接近液滴噴射入口。由于冷氣初始溫度和幾何模型壁面溫度都均為203 K，而液滴溫度為常溫300 K，因此液滴在與冷氣接觸后，溫度會很快下降。因為流化床中心部位是氣體的噴射區，所以中間部位的溫度很低，由中心向兩邊溫度逐漸升高，而在壁面處，由于液滴的回流，會使得液滴能量損失，溫度與壁面溫度接近，因此出現流化床內接近壁面處溫度陡降，這與耿縣如等[17]所做關于液滴噴霧冷凍的溫度變化和分布規律相類似。

3.2 霧化液滴的運動

圖4為液滴在氣液兩相流的霧化特性圖。由圖4a可以看出，液滴從入口進入流化床內，液滴均具有一定初速度，因此液滴會很快到達流化床底部壁面，碰到壁面后，由于沖量作用，其方向發生了改變，這就會使得碰到流化床底部的液滴產生向上的回流，如圖4b所示。同時使得液滴的速度呈現出沿軸向逐漸減小，沿徑向中心高兩邊低的現象，如圖4c所示。這說明在液滴霧化的過程中，由于幾何模型結構的作用，會產生一定的回流這將對液滴霧化產生影響。同時比較圖4c和圖4d也可以看出，PBM模型和DPM模型在計算液滴霧化過程中有著相同的速度場分布，這與Taghipour等[13]對氣固流化床的研究結論是一致的。同時PBM又可以用于液滴的粒徑分布研究，因此本文采用了PBM模型來研究液滴的粒徑變化和分布情況。

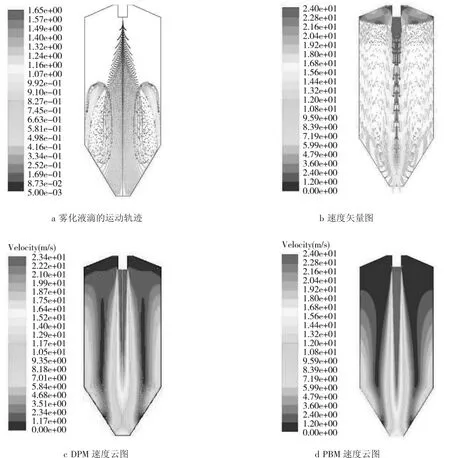
圖4液滴在氣液兩相流的霧化特性Fig.4 Atomization characteristics of droplets in gas-liquid two-phase flow

3.3 液滴的速度

圖5為液滴X方向速度隨Y坐標的變化圖。

霧化液滴之間會出現團聚和破碎的現象，這直接關乎液滴的霧化效果，同時也會對流化床包覆的研究產生影響。速度和溫度的分布對霧化液滴的團聚和破碎有著很大影響。

圖5a、5b說明了PBM和DPM模型在對液滴霧化進行計算過程中，在軸向上不同位置液滴軸向速度從Y=0處向壁面接近的變化。液滴的初速度為25 m/s，液滴噴出后，在幾何模型的中部，液滴有能量損失，因此圖中液滴在X=0 m處速度為23 m/s，并且越接近幾何體壁面，液滴的速度越小。在Y=0.21 m處液滴速度為零，從Y=0.21 m處到壁面即Y=0.4 m處，液滴速度方向改為向上，這是因為液滴在碰到壁面以后出現了回流現象，回流又會導致液滴之間的接觸和碰撞。這一現象將會使液滴的粒徑發生變化，同時由圖可知，2種模型的計算結果吻合，這也說明了由圖4c、d得出的可以用PBM來研究液滴的粒徑變化和分布情況的結論。

3.4 液滴的粒徑分布

本文中粒徑分布是指液滴在某種粒徑下的液滴數量，其具體分布情況如圖6所示。

圖6a、b、c表明了霧化液滴軸向上不同位置的粒徑分布，液滴的初始粒徑為1.26 μm。由圖可知，液滴在霧化過程中發生了團聚和破碎現象，形成了粒度不一的分布。團聚體數量最大的粒徑范圍為2.4～3 μm，最小范圍為0～0.5 μm。在軸向上，離噴口越遠處，液滴的團聚現象越明顯，即2.4～3 μm的液滴數量越多，而0～0.5 μm、0.5～0.79 μm的液滴數量比較少。這是因為在流化床的中心部位氣體的溫度，速度較大，而隨著液滴向流化床邊緣不斷的運動，液滴出現了團聚和破碎的現象如圖6d所示，ddroplet表示液滴的粒徑。由液滴的累積粒度曲線可以看出，液滴在噴口處和末端部位的數量是最多的，這主要是因為在流化床頂部接近入口處液滴速度較大，而在接近底部椎體部分液滴的碰撞比較明顯，碰撞后形成的小顆粒數量較多。

圖5 液滴X方向速度隨Y坐標的變化Fig.5 Change of X direction velocity of droplet with Y coordinate

圖6霧化液滴的粒徑分布Fig.6 Particle size distribution of atomized droplets

圖6b表示的是X=1.37 m直線上的液滴在徑向由中心向兩邊運動的過程中，1.8～2.4、0.6～1.2 μm粒徑的液滴數量的變化。由圖可知，由于初始粒徑為1.26 μm，在Y=0～0.2 m的過程中，液滴同時存在團聚和破碎現象，因此才會出現了1.8～2.4、0.6～1.2 μm的液滴數量不斷增加的現象。在Y=0.2 m處以后流化床內的溫度開始越來越接近壁面溫度即T=203 K，因此顆粒的溫度開始逐漸降低出現凝固現象，團聚后難以破碎，2.5～3 μm的液滴數量分布比較多，所以1.8～2.4、0.6～1.2 μm的液滴，尤其是1.8～2.4 μm的數量在這一區域比較少（說明：霧化的液滴在實際過程中由于噴嘴的作用，液滴可以被分散成很細小的單個液滴，出現幾微米的液滴屬合理現象）。

綜上所述，由模擬結果可知，液滴在霧化過程中，由于流化床壁面和入口氣體的溫度都為203 K，與液滴初始溫度相差較大，因此接近壁面處流化床內溫度會出現陡降。同時由于液滴的初速度為28 m/s，因此液滴在短時間內到達底部椎體部分，產生回流，造成液滴自身的能量損失，而這將會使接近壁面處的液滴出現大量團聚。

4 結論

本文中基于CFD中的群體平衡模型對流化床內液滴的霧化行為進行了二維數值模擬，并與離散相模型的計算結果進行對比，結果表明，群體平衡模型和離散相模型可以得出相同的速度場分布，群體平衡模型可以進一步得出更為詳細的粒徑分布，故群體平衡模型可以作為離散相模型的替代模型進一步研究液滴的聚并和破碎行為。

流化床內溫度呈現中間低、兩邊高的狀況，在液滴碰到錐形壁面時液滴產生回流，液滴在這一區域很容易團聚。在中心區域液滴速度較大，破碎現象比較明顯。

（

）：

[1]張建林，劉邱祖，賴成，等.液滴在固體表面流動特性的數值模擬及驗證[J].中國粉體技術，2016（3）:19-21.

[2]NIENOWA W.Fluidised bed granulation and coating:applications to materials，agriculture and biotechnology[J].Chemical Engineering Communication，1995，139：233-253.

[3]LITSTER J，ENNIS B.The science and engineering of granulation processes[J].Particle Technology，2004，15.

[4]LINK K C，ERNST-ULRICH S.Fluidized bed spray granulation investigation of the coating process on a single sphere[J].Chemical Engineering and Processing 1997，36：443-457.

[5]MUBASHIR，HUSSAIN，JITENDRA，et al.A new framework for population balance modeling of spray fluidized bed agglomeration[J].Particuology，2015，19（2）:141-154.

[6]REYNOLDS G K.Modelling of pharmaceutical granule size reduction in a conical screen mill[J].Chemical Engineering Journal，2010，164（2/3）:383-392.

[7]GRIFFIN D W，MELLICHAMP D A，DOHERTY M F.Reducing the mean size of API crystals by continuous manufacturing with product classification and recycle[J].Chemical Engineering Science，2010，65（21）:5770-5780.

[8]MORTIER S T F C，GERNAEY K V，BEER T D，et al.Development of a population balance model of a pharmaceutical drying process and testing of solution methods[J].Computers&Chemical Engineering，2013，50（9）:39-53.

[9]BASHEER I A，HAJMEER M.Artificial neural networks:fundamentals，computing，design，and application[J].Journal of Microbiological Methods，2000，43（1）:3.

[10]孫國祥，汪小旵，丁為民.基于CFD離散相模型霧滴沉積特性的模擬分析[J].農業工程學報，2012，28（6）:13-19.

[11]梁欽，高貴軍，劉邱祖.壓力型霧化噴嘴射流噴霧氣-液兩相流數值模擬[J].中國粉體技術，2015，21（2）:5-9.

[12]DUANGKHAMCHAN W，RONSSEWF，DEPYPERE F，et al.CFD study of droplet atomisation using a binary nozzle in fluidised bed coating[J].Chemical Engineering Science，2012，68（1）:555-566.

[13]TAGHIPOUR F，ELLIS N，WONG C.Experimental and computational study of gas solid fluidized bed hydrodynamics[J].Chemical Engineering Science，2005，60（24）:6857-6867.

[14]BARRASSO D，TAMRAKAR A，RAMACHANDRAN R.A reduced order PBM ANN model of a multi-scale PBM DEM description of a wet granulation process[J].Chemical Engineering Science，2014，119（119）:319-329.

[15]侯廣信，陳建義.顆粒碰撞團聚對旋風分離器分離性能影響研究[J].石油機械，2008，36（5）:1-4.

[16]MCGRAWR.Description of aerosol dynamics by the quadrature method of moments[J].Aerosol Science&Technology，1997，27（2）:255-265.

[17]耿縣如，徐慶，李占勇，等.噴霧冷凍法單個液滴凍結過程模擬[J].化工進展，2012，31（5）:981-986.