小波-支持向量機組合算法在地鐵沉降預測中的應用

(中鐵工程設計咨詢集團有限公司，北京 100055)

地鐵為緩解城市的交通壓力，提高城市通行效率作出了巨大貢獻。地鐵結構位于地下空間，容易受到列車振動、周圍地質條件等外界因素的影響而發生沉降[1，2]。當沉降變形超過一定的限度，勢必會影響列車運行的平順度，嚴重時可能會影響地鐵的運營安全。因此，進行持續性的沉降監測和預報對于地鐵的安全運營和維護具有重要意義。

精確提取地鐵沉降監測信息并做出可靠預報能夠為后續安全決策提供關鍵信息，最大限度地減少沉降變形帶來的危害[3]。地鐵沉降受到諸多因素的影響，且難以用一定的函數模型描述。同時，現有監測手段容易受到周圍環境的干擾，監測數據存在一定的誤差，如何準確提取監測數據中的穩定信息并以此為基礎做出可靠的預測成為熱點問題[4]。基于前期觀測數據建立數學模型，對未來沉降趨勢做出一定時間段的預測是目前常用的方法，如神經網絡法、灰色系統理論、支持向量機、時間序列模型等[5-7]。其中，基于結構風險最小化原理的支持向量理論具有較好的泛化能力。利用小波分析理論對實際觀測數據進行降噪處理，將降噪后的沉降監測信息用于支持向量機沉降預測，其預測精度優于單獨使用支持向量機沉降預測。

1 小波分析

對于地鐵沉降監測數據X(t)，由于在觀測過程中，儀器不可避免地受到周圍環境以及人為操作誤差的影響，其中含有一定的隨機誤差，則沉降數據可以表示為

X(t)=f(t)+ε

(1)

其中，f(t)為觀測數據中的有用信息，ε為觀測數據中的隨機噪聲[8]。小波分析是一種時域和頻域都可以變化的分析方法，具有局部化分析的功能[9]。根據小波分析的定義，序列X(t)與小波函數的內積為

W(a，b)={X(t)，ψa，b(t)}=

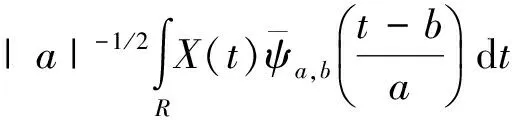
(2)

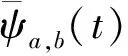
(3)

2 支持向量機

支持向量機理論(Support vector machine，SVM)是Vapnik團隊在1995年提出的一種模式識別方法，其基本原理基于統計學中結構風險最小化原則，具有很強的泛化能力，能夠在樣本量較小的情況下做出最優決策[10-12]。支持向量機理論的基本思想是將已知信息投影到高維超平面上，在高維空間將機器學習的正例和反例距離最大化。

SVM具體計算過程中，需要利用函數f(x)=wx+b對原始數據進行擬合，擬合函數為

(4)

其中αi和b通過優化公式求得

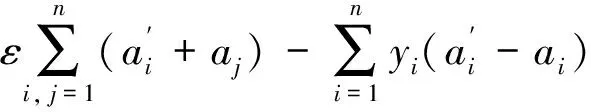
(5)

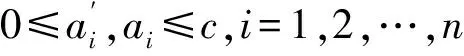
在利用SVM對實際數據進行處理時，需要根據數據特性選擇合適的懲罰函數和損失函數。求得上述參數后，將參數帶回公式(4)中得到決策函數，即可獲得最優的決策結果。

3 工程實例

為了檢驗小波-支持向量機組合算法在實際工程分析中的效果，基于某地鐵監測點25期沉降數據進行工程實例分析。其中，每期數據間隔為7 d，前20期用于監測模型的建立，后5期進行沉降預測。分別采用單獨SVM方法和小波-支持向量機方法(W-SVM方法)對后5期沉降數據進行預測，將預測結果與實際觀測數據進行對比，分析其預測精度。

3.1 小波去噪

實際沉降監測過程中，受周圍環境的干擾，監測數據中通常存在不規則的隨機誤差，會影響沉降數據分析的準確性和可靠性。因此，首先利用小波分析方法對地鐵的沉降監測數據進行分解降噪處理，以獲得較為可靠穩定的沉降信息。

采用小波進行4尺度分解，選擇合適分量進行小波重構，得到去噪后的重構序列。圖1為原始監測時間序列和小波去噪后的平滑序列。原始監測序列含有較多突起，并不平滑，不符合地鐵的沉降變化規律。經過小波去噪后，整體曲線平滑，趨勢明顯，有利于后續分析。

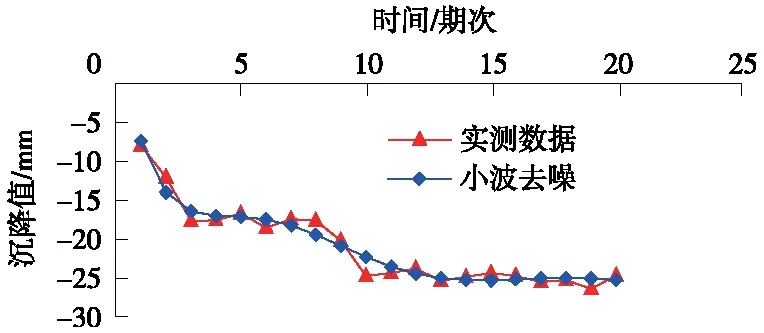
圖1 原始監測數據和小波降噪結果對比

3.2 沉降預測

以前20期原始沉降監測數據和去噪數據作為支持向量機訓練集，對21～25期沉降數據進行預測，將預測結果與實際觀測數據進行對比，分析兩種方法的精度和可靠性。

圖2為實際檢測數據、SVM預測、W-SVM預測結果的時間序列對比。由于1～20期的原始序列存在一定的波動，導致SVM預測結果與實際監測數據有較大偏差，而W-SVM采用小波去噪后的數據進行訓練，其預測結果與實際觀測數據更為接近，預測精度較高。

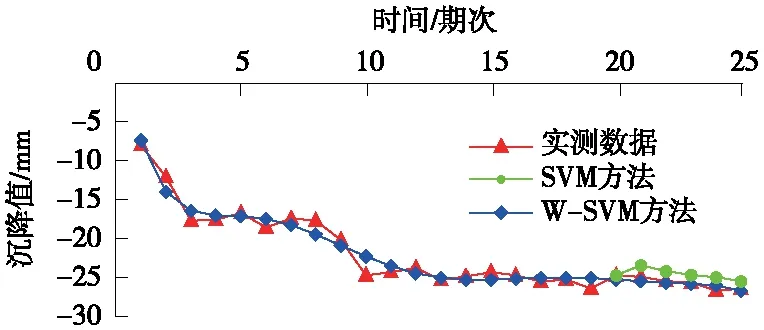
圖2 SVM和W-SVM預測結果與實際觀測結果的對比

3.3 精度統計

圖3 SVM和W-SVM預測誤差時間序列

以實際觀測數據為真值，對兩種預測方法的21～25期預測數據進行誤差統計。圖3為兩種預測方法結果的誤差時間序列，SVM方法預測結果誤差較大(-1.5 mm左右)，且存在一定的系統偏差。而W-SVM方法預測誤差在0附近波動，誤差分布在[-0.5，0.5] mm之間。表1為兩種預測方法的具體誤差統計。從表1可以看出，SVM方法的預測相對誤差在3.75%至6.37%之間，而W-SVM方法的預測相對誤差在0.58%至2.39%之間。綜上所述，基于小波分析去噪+支持向量機方法的預測精度明顯高于單獨的支持向量機方法。

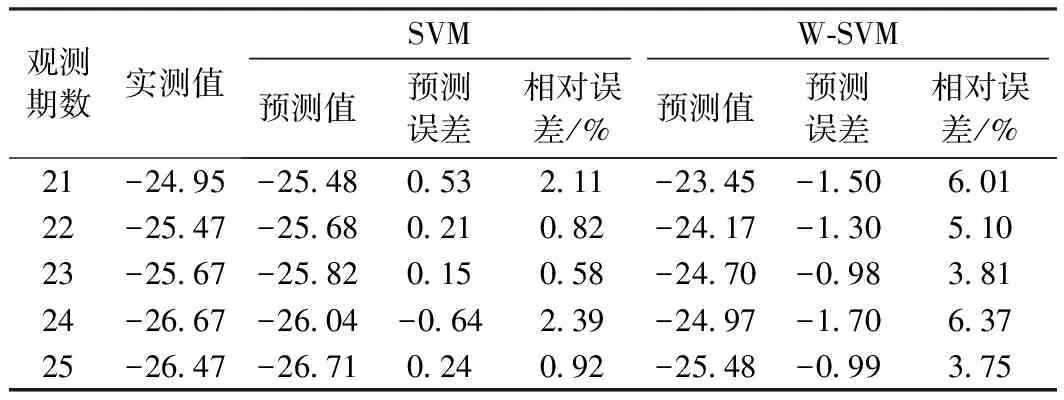
表1 SVM和W-SVM預測誤差統計 mm

4 結論

采用具有時頻域分析功能的小波算法對原始監測數據進行處理，得到較為平滑穩定的沉降信息，然后將去噪后的信息建立SVM訓練集，對后續沉降變化做出預測。與單獨SVM預測結果相比，W-SVM方法預測精度更高，不受局部隨機誤差的影響，預測誤差較小且沒有明顯的系統偏差。工程實例結果顯示，基于小波-支持向量機組合算法的地鐵沉降預測方法能夠有效抑制觀測數據中隨機誤差的影響。

[1] 張明希，許捍衛，葛文.基于小波分析與支持向量機的地鐵隧道沉降預測[J].工程勘察，2013，41(12):57-60

[2] 黃騰，孫景領，陶建岳，等.地鐵隧道結構沉降監測及分析[J].東南大學學報(自然科學版)，2006，36(2):262-266

[3] 李金鋒.遺傳BP神經網絡在地鐵工程沉降預測中的應用[D].北京：中國地質大學(北京)，2006

[4] 王堅，高井祥，鄭南山.基于小波理論的沉降監測數據序列分析[J].大地測量與地球動力學，2005，25(4):91-95

[5] 楊敏，盧俊義.基坑開挖引起的地面沉降估算[J].巖土工程學報，2010，32(12):1821-1828

[6] 劉杰，姚海林，任建喜.地鐵車站基坑圍護結構變形監測與數值模擬[J].巖土力學，2010(S2):456-461

[7] Mendes R， Mohais A S. DynDE: a differential evolution for dynamic optimization problems[C]∥Evolutionary Computation， 2005. The 2005 IEEE Congress on. IEEE， 2005，3：2808-2815

[8] 薛茹，毛靈濤，安里千.小波分析在動態實驗數據處理中的應用[J].湖南科技大學學報(自然科學版)，2007，22(1):59-62

[9] 劉明才.小波分析及其應用[M].北京：清華大學出版社，2013

[10] 張瀟瓏.基于自適應粒子群優化的SVM算法在建筑物沉降預測中的應用[J].測繪工程，2015(11):44-47

[11] 李鵬，高波.小波時間序列在廣州地鐵沉降監測數據處理中的應用[J].城市勘測，2012(2):156-159

[12] 王劉準，邱衛寧，花向紅，等.小波時間序列分析在高鐵沉降變形中的應用[J].測繪地理信息，2013，38(4):45-47