星間單差GPS實時精密衛星鐘差估計及精度分析

牟春霖

(中國鐵路設計集團有限公司，天津 300142)

1997年，美國噴氣動力實驗室(JPL)的Zumberge等人提出了精密單點定位(Precise Point Positioning，簡稱PPP)技術[1-3]。經過多年的發展，PPP技術的后處理靜態定位精度可以達到厘米級，動態精度可達厘米至分米級[4-6]。然而，后處理PPP技術的定位時效性受制于事后精密軌道與鐘差(如IGF、IGR)產品的延遲[7]；超快速衛星星歷與鐘差產品(IGU)雖然可以滿足PPP對于時效性的要求，但是其衛星鐘差產品精度較差，不能滿足某些生產對于精度的要求。基于PPP技術存在的上述問題，近年來，基于實時精密軌道和鐘差產品的精密單點定位技術[8-10]成為國內外學者研究的熱點之一。

利用GNSS區域參考站網數據，建立基于星間單差的觀測模型，利用IGU實時預報軌道，采用序貫最小二乘參數估計方法，對GPS衛星鐘差進行實時解算，并將解算的GPS衛星鐘差與IGS事后精密衛星鐘差進行對比分析；然后，將實時解算的GPS衛星鐘差用于不同區域站點的實時精密單點定位中，并將定位結果與IGS提供的準確坐標進行比較和分析，對實時解算的GPS衛星鐘差的精度及作用范圍進行探討。

1 數學模型

星間單差模型是在非差消電離層組合觀測方程的基礎上構造的，首先選擇一顆衛星作為參考衛星，其他衛星的觀測值與參考衛星觀測值作差，可以得到星間單差模型[11，12]的觀測方程，如式(1)、式(2)所示

(1)

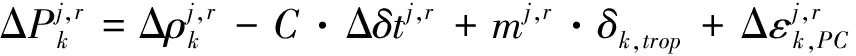
(2)

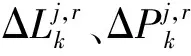
星間單差模型消除了接收機鐘差參數，避免了同時求解接收機鐘差和衛星鐘差時產生的秩虧現象。從星間單差的觀測方程可以看出，相對衛星鐘差與相對衛星模糊度之間存在較強的相關性，在解算時，很難在短時間內將兩者有效分離。可在傳統星間單差模型的基礎上附加歷元間差分模型，以消除初始相位模糊度對衛星鐘差參數解算的影響。

初始歷元和第二歷元及以后歷元星間單差的載波相位及偽距觀測方程分別如式(3)～式(6)所示

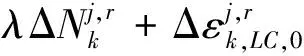
(3)

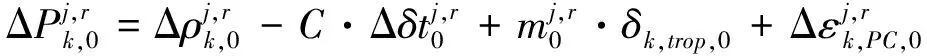
(4)

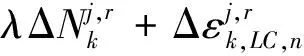
(5)

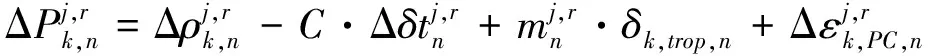
(6)

式中，0代表初始歷元；n代表第二及以后歷元。

聯合式(3)、式(4)及式(5)、式(6)，對第n歷元構造新的觀測方程，如式(7)所示

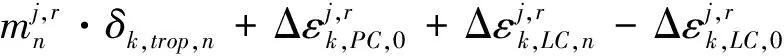
(7)

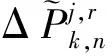
將式(7)進行變換，可以得到新構造觀測模型的誤差方程，如式(8)、式(9)所示

V=B·dΔX-L

(8)

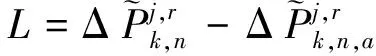
(9)

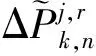
幾個朋友探討目前創業環境問題時，有人說：“沒有系統的鼓勵年輕人創業，是浪費資源且不切實際的。”這一點讓我好好思考了一下這些年自己創業，以及輔導年輕人創業的經驗。

根據衛星的高度角對各衛星觀測數據賦予不同的權值。若定義權矩陣為P，則觀測模型的法方程如式(10)所示

BT·P·B·dΔX=BT·P·L

(10)

由于GNSS區域參考站網中各測站間的距離較近，測站間的對流層延遲相關性較強，如果同時對多個測站的觀測數據進行聯合平差解算，會使解算方程產生病態性。首先在每個測站對衛星鐘差進行實時解算，然后對單站解算的衛星鐘差進行加權聯合處理，得到最終的衛星鐘差結果。在加權處理時，依據測站的非參考衛星和參考衛星的高度角進行定權，如式(11)、式(12)所示

(11)

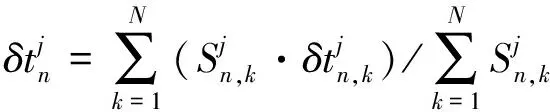
(12)

2 數據處理和結果分析

2.1 鐘差解算

借助作者研制的基于星間單差的實時衛星鐘差估計程序，基于GNSS區域參考站網數據，采用序貫最小二乘參數估計方法，對GPS衛星鐘差進行實時解算；然后，將解算的衛星鐘差與IGS最終鐘差產品進行精度對比，并對影響衛星鐘差解算精度的因素進行分析。

選取中國國家海洋局GNSS業務觀測系統的5個測站(分別為NCST、NLHT、NLKO、NQHD及NZMW)作為區域參考站網(如圖1所示)，區域參考站網中測站的觀測數據為2009年11月3日24 h的數據，數據采樣率為30 s。

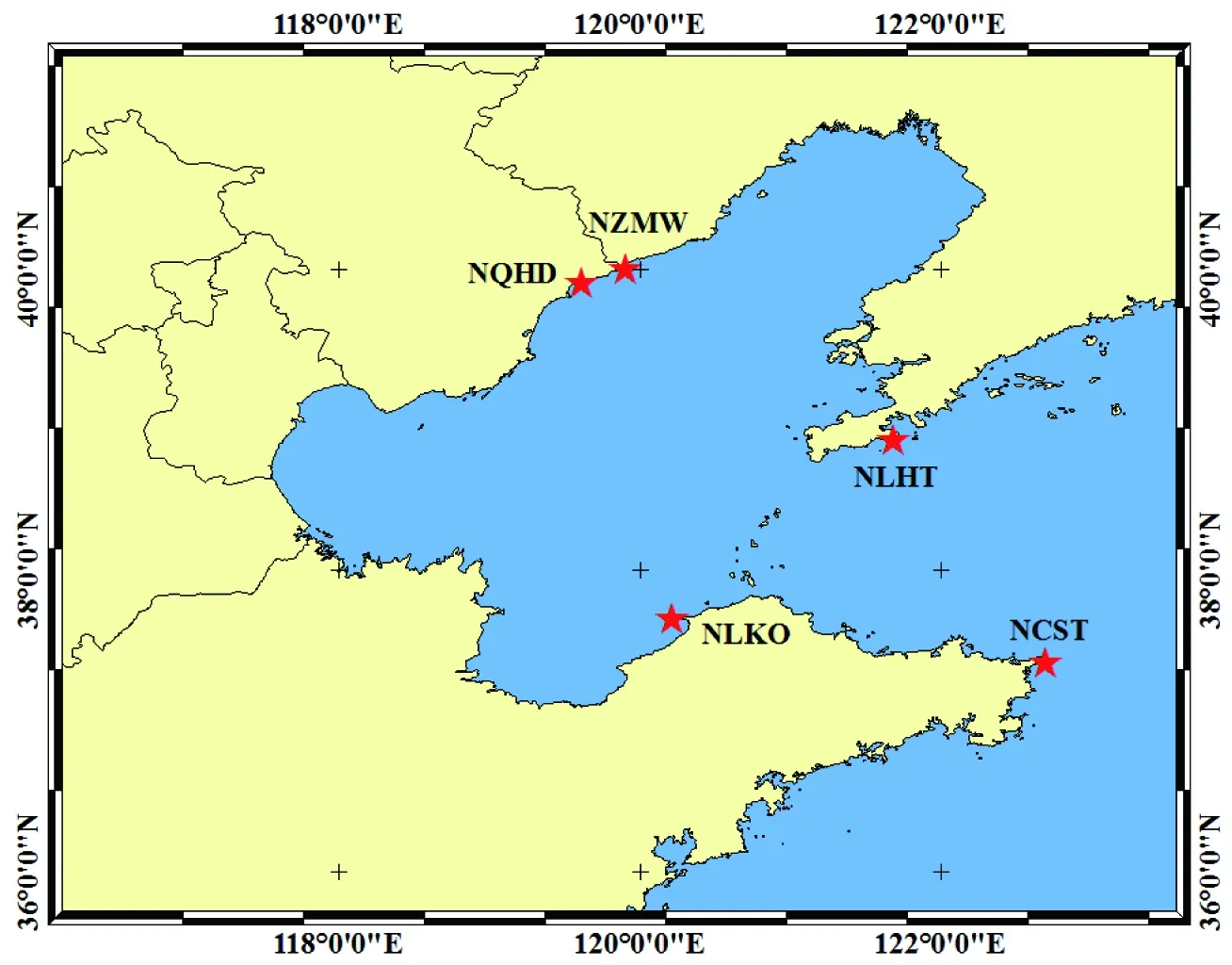
圖1 GPS衛星鐘差估計區域參考站網站點分布

以1 h為時間窗口對GPS衛星鐘差進行實時解算，選取時間窗口內高度角最大的衛星作為參考衛星，其他衛星為非參考衛星，解算得到非參考衛星的相對衛星鐘差結果，然后，將解算的衛星鐘差與IGS事后鐘差產品進行精度的對比。由于篇幅的限制，僅選取兩個時段(1～2 h和3～4 h)的解算結果進行精度的對比和分析。

解算的GPS相對衛星鐘差與IGS事后相對衛星鐘差之差如圖2和圖3所示。對1～2 h以及3～4 h時間窗口解算的衛星鐘差與IGS事后衛星鐘差之差進行誤差統計，如表1和表2所示。

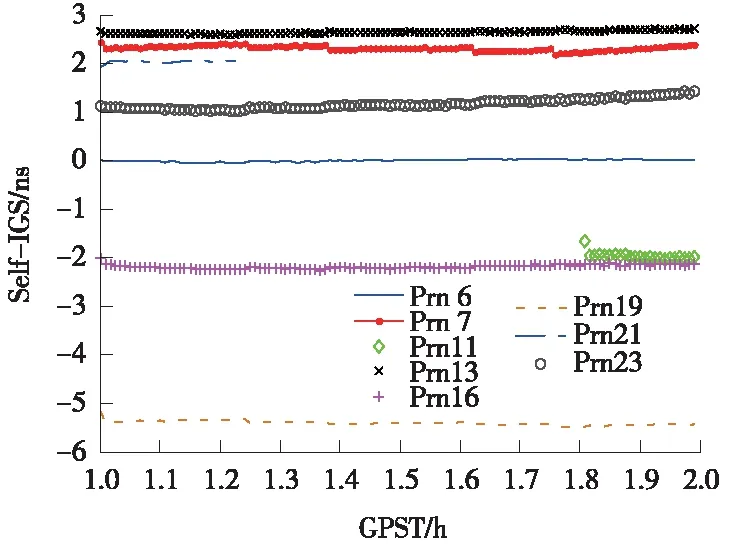
圖2 1～2 h時間窗口解算的GPS相對衛星鐘差與IGS相對衛星鐘差產品之差

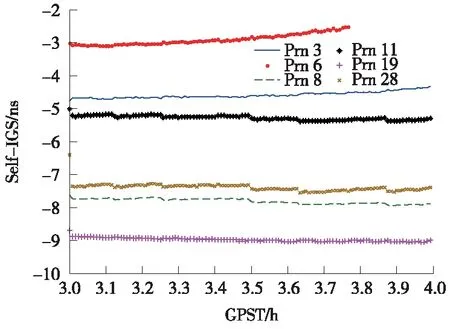
圖3 3～4 h時間窗口解算的GPS相對衛星鐘差與IGS相對衛星鐘差產品之差

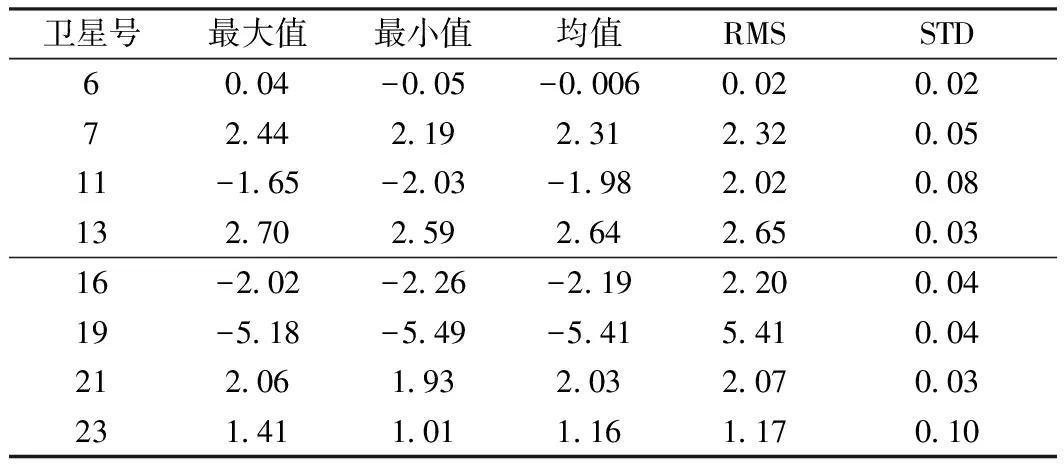
表1 1～2 h時間窗口解算的GPS相對衛星鐘差誤差統計 ns

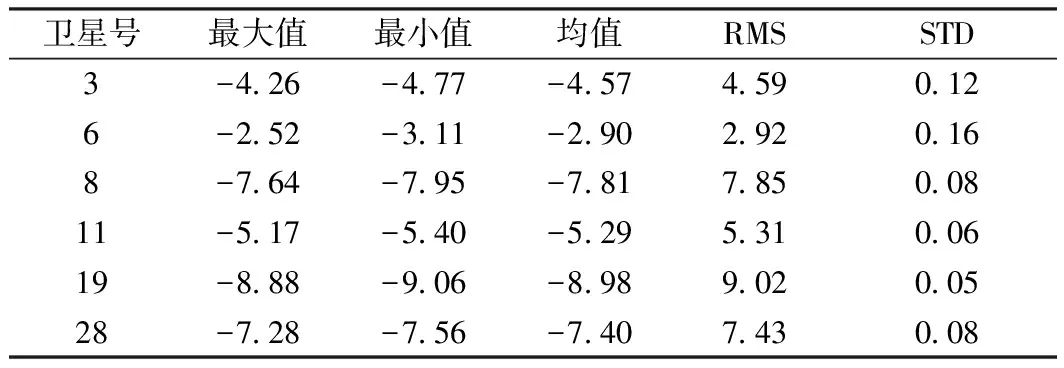
表2 3～4 h時間窗口解算的GPS相對衛星鐘差誤差統計 ns

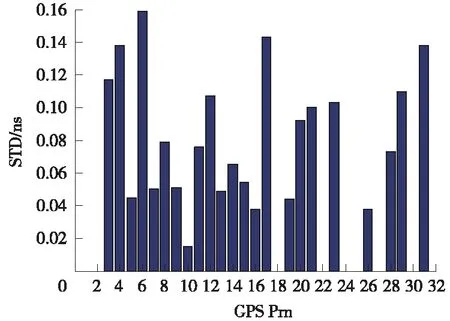
圖4 所有GPS相對衛星鐘差標準差(STD)

表3 所有GPS相對衛星鐘差的STD統計 ns

從圖2、圖3及表1、表2可以看出，由于初始歷元偽距觀測值其他誤差項的影響，解算的GPS相對衛星鐘差與IGS事后相對衛星鐘差相比，每顆衛星的相對衛星鐘差均方根誤差(RMS)普遍較大，但其為一固定值，可被精密單點定位模糊度浮點解吸收，并不影響PPP定位結果的精度，影響PPP解算結果精度的誤差項為衛星鐘差的標準誤差(STD)。

從圖4及表3的整體解算結果來看，大部分衛星的相對衛星鐘差解算精度(STD)優于0.12 ns，少數衛星的相對衛星鐘差解算精度較低，但是均優于0.16 ns，能夠滿足厘米級精度實時PPP的應用要求。

2.2 鐘差估計精度影響因素分析

從鐘差解算模型來看，可能影響衛星鐘差解算精度的因素有測站觀測數據質量及IGU實時預報軌道(包括參考衛星及非參考衛星)的精度，而數據質量直接體現在衛星的高度角上。以1～2 h及3～4 h時間窗口為例，分別對兩個時間窗口GPS衛星的高度角和參考衛星及非參考衛星IGU實時預報軌道的誤差進行統計并進行分析。衛星高度角及IGU實時預報軌道的精度如圖5～圖8所示。

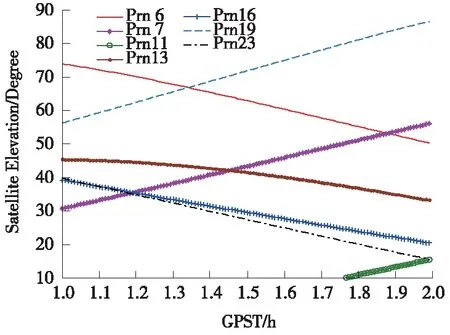
圖5 1～2 h時間窗口GPS衛星的高度角

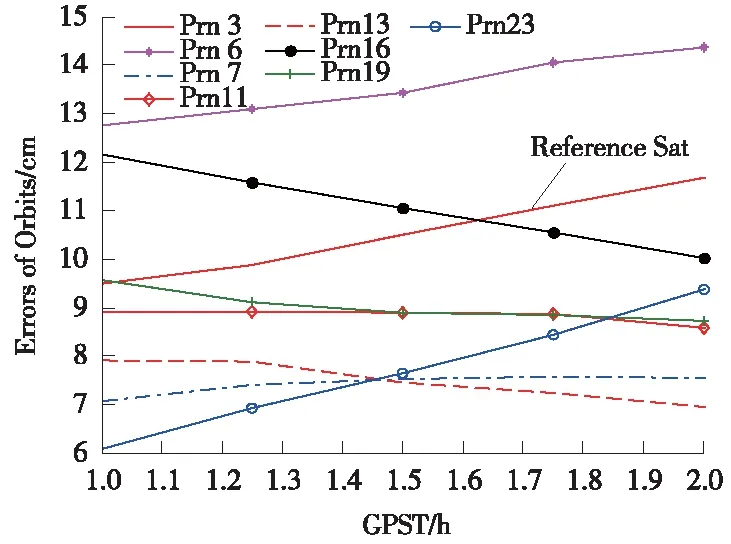
圖6 1～2 h時間窗口衛星軌道誤差

圖7 3～4 h時間窗口GPS衛星的高度角

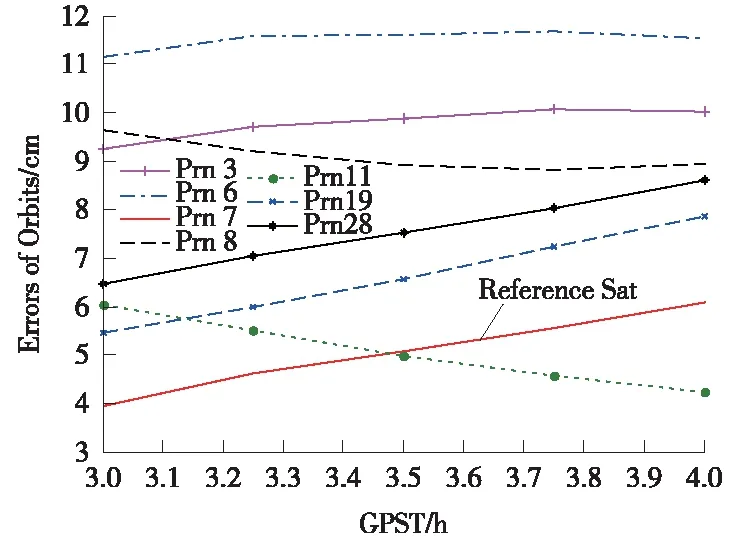
圖8 3～4 h時間窗口衛星軌道誤差

從圖5～圖8可以看出，參考衛星與非參考衛星的軌道誤差精度相當，在構造星間單差觀測模型時，以非參考衛星與參考衛星觀測值作差，可大大降低軌道誤差對相對衛星鐘差解算精度的影響，結合表1及表2的衛星鐘差誤差統計結果可以看出，星間單差的軌道誤差對鐘差解算精度影響較小。

1～2 h時間窗口解算的GPS相對衛星鐘差誤差(STD)最大的衛星分別為11號和23號，其他衛星的相對衛星鐘差誤差較小，結合圖5中各衛星的高度角進行分析，11號衛星的高度角一直小于20°，23號衛星的高度角一直處于下降趨勢，1.8 h時已經小于20°，其他衛星的高度角一直較大；3～4 h時間窗口解算的GPS相對衛星鐘差誤差(STD)最大的衛星分別為3號和6號，其他衛星相對衛星鐘差誤差較小，結合圖7各衛星的高度角進行分析，3號和6號衛星的高度角一直在減小，并且分別在3.3h和3.7 h時低于20°，其他衛星的高度角一直較大或一直處于上升狀態。

綜上所述，當衛星高度角一直處于下降趨勢，特別是當衛星高度角小于20°時，測站接收機接收到的GPS觀測數據噪聲較大，會直接對鐘差解算精度產生較大的影響；另外，當參考衛星與非參考衛星的軌道誤差精度相當時，構造的星間單差觀測模型可將非參考衛星與參考衛星的軌道誤差相互抵消，大大降低了軌道誤差對鐘差解算精度的影響。

2.3 PPP結果及精度分析

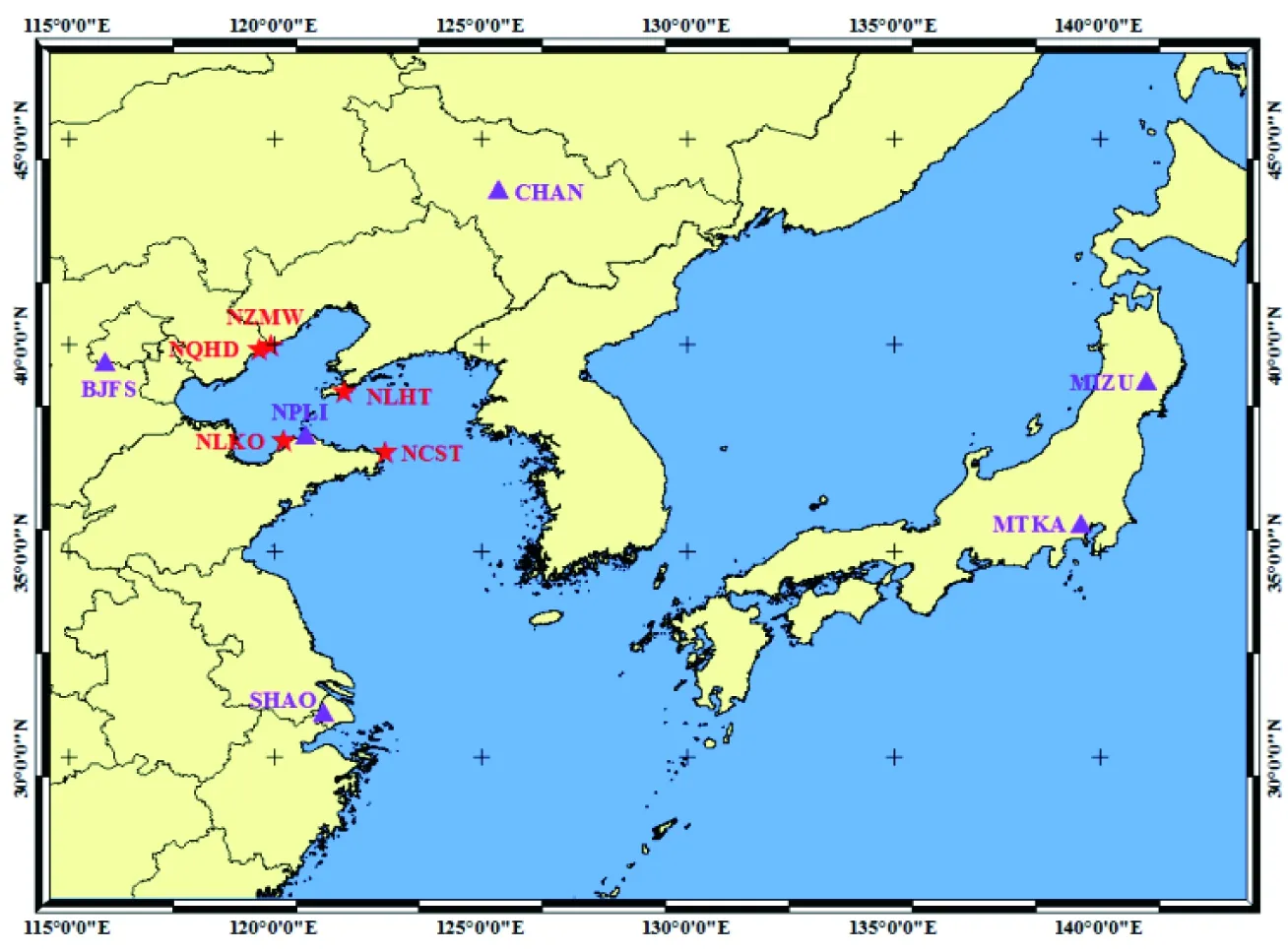
圖9 GPS實時精密單點定位站點分布

為了分析解算的衛星鐘差對實時PPP解算精度的影響，并分析鐘差作用的距離，將解算的衛星鐘差用于不同站點的GPS實時精密單點定位中，通過各站點PPP精度的對比，探討基于區域參考站網估計的衛星鐘差的可擴展性。試驗方案站點分布如圖9所示，用于試驗的6個測站分別為BJFS、NPLI、CHAN、SHAO、MIZU、MTKA。其中，BJFS和NPLI與鐘差估計站網中心距離小于500 km，CHAN與SHAO與鐘差估計站網中心距離為500～1 000 km，MIZU和MTKA與鐘差估計站網中心距離大于1 000 km。

以1～2 h時間窗口為例，將解算的衛星鐘差數據用于上述6個站點的實時PPP中，將解算的各站點坐標與IGS提供的精確坐標進行對比，得到兩者之間的坐標差(dN，dE，dU)，如圖10所示。將上述坐標差進行誤差統計，見表4。

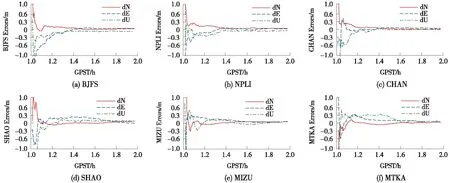
圖10 各測站PPP坐標差

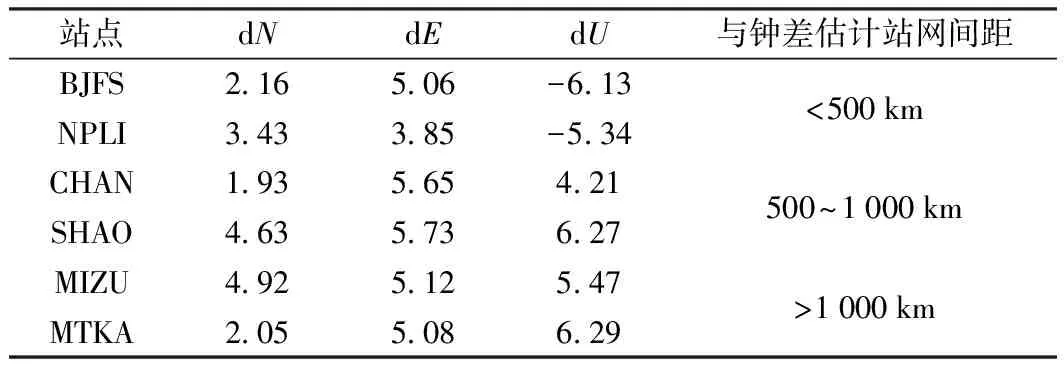
表4 各測站PPP結果誤差統計 cm

由圖10及表4數據可以看出，各測站PPP收斂情況較好，GPS實時精密單點定位的結果并不受衛星鐘差系統誤差的影響，驗證了2.1節中提出的GPS衛星鐘差的系統誤差可被PPP模糊度浮點解吸收的結論；由表4各站點與鐘差估計站網間距及PPP誤差統計結果可以看出：各站點的水平分量精度均優于6 cm，高程分量精度均優于7 cm，表明解算的衛星鐘差能夠滿足厘米級精度實時精密單點定位的應用要求；另外，即使PPP站點距離鐘差估計區域參考站網較遠(>1 000 km)，PPP解算精度也較高，表明估計的實時衛星鐘差作用距離較遠，可擴展性強。

3 結論

基于星間單差觀測模型建立衛星鐘差解算模型，采用GNSS區域參考站網數據，借助自編程序進行GPS實時衛星鐘差的解算及精度分析。衛星鐘差解算結果表明，所有衛星的相對衛星鐘差精度(STD)均優于0.16ns，能夠滿足厘米級精度實時PPP的應用要求。對影響衛星鐘差解算精度的因素進行了分析，結果表明，當衛星高度角處于較低水平，特別是小于20°時，測站接收機接收到的GPS觀測數據噪聲較大，會直接對鐘差解算精度產生較大的影響；另外，當參考衛星與非參考衛星的軌道誤差精度相當時，構造的星間單差觀測模型可將非參考衛星與參考衛星的軌道誤差相互抵消，大大降低了軌道誤差對鐘差解算精度的影響。為了分析解算的衛星鐘差對實時PPP精度的影響及衛星鐘差作用距離，將解算的相對衛星鐘差用于不同站點的實時PPP中，試驗結果表明，各站點的水平分量精度均優于6 cm，高程分量精度均優于7 cm，各站點PPP解算精度并不隨站點與鐘差區域參考站網距離的增大而明顯降低，說明解算的GPS衛星鐘差能夠滿足厘米級精度實時PPP的應用要求，鐘差的作用距離遠，可擴展性較強。

[1] Zumberge J F， Heflin M B， Jefferson D C， et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research Solid Earth， 1997，102(B3):5005-5017

[2] 李浩軍，王解先，胡叢瑋，等.基于歷元間差分技術的精密單點定位研究[J].宇航學報，2010，31(3):748-752

[3] 易重海.實時精密單點定位理論與應用研究[D].長沙：中南大學，2011

[4] 劉焱雄，彭琳，周興華，等.網解和PPP解的等價性[J].武漢大學學報(信息科學版)，2005，30(8):736-738

[5] 易重海，陳永奇，朱建軍，等.一種基于IGS超快星歷的區域性實時精密單點定位方法[J].測繪學報，2011，40(2):226-231

[6] 范士杰，秦學彬，吳紹玉，等.不同星歷和鐘差產品的PPP驗潮試驗及結果分析[J].海洋測繪，2014，34(4):43-46

[7] Kouba J. A guide to using International GPS Service (IGS) products[J]. Maryland Biological Stream Survey Data Versar Inc， 2003，4(3):106

[8] Muellerschoen R J， Barsever Y E， Bertiger W I， et al. DECIMETER ACCURACY: NASA’S GLOBAL DGPS FOR HIGH-PRECISION USERS[J]. Gps World， 2001，12

[9] 李星星.GNSS精密單點定位及非差模糊度快速確定方法研究[D].武漢：武漢大學，2013

[10] 宋偉偉.導航衛星實時精密鐘差確定及實時精密單點定位理論方法研究[D].武漢：武漢大學，2011

[11] 高旺，高成發，潘樹國，等.基于區域參考站網絡的精密衛星鐘差估計及其在實時精密單點定位中的應用[J].東南大學學報(自然科學版)，2013(S2):400-405

[12] Gao C， Gao W， Pan S， et al. High-Precision Oceanic Real-Time Positioning Application Based on Regional Continuous Operation Reference Stations[J]. Journal of Coastal Research， 2015，73：325-330