基于模糊神經網絡的油氣運輸管道調度技術

王 子， 朱朋勇

(中石油管道有限責任公司 西氣東輸分公司, 杭州 310006)

引言

油氣管道是油氣運輸的重要載體，油氣運輸管道網絡的優化節點部署設計是保障油氣運輸網絡可靠穩定運行的關鍵，通過對油氣運輸管道網絡的優化路徑規劃和調度設計，降低管道部署的開銷，提高油氣運輸的吞吐性能。油氣運輸管道網絡具有自組織性，以各個壓氣站為節點進行全局網絡設計，在整個管道組網設計中，受到地理環境、用戶分布情況以及壓氣站分布情況等各種因素的影響，導致油氣運輸管道運輸調度變得復雜，油氣運輸的管道調度是一項系統性的綜合網絡工程，需要研究一種優化的油氣運輸管道調度技術，提高油氣運輸管道的全局穩定性和暢通性，保障大型油氣運輸工程的安全穩定運行[1]。

對油氣運輸管道調度是建立在對管道網絡的綜合節點定位和路由優化設計基礎上的，通過建立管道網絡的無線組網結構模型，采用自適應傳感器組網設計方法進行路由分發設計，提高管道網絡的連通性和覆蓋能力，傳統方法中，對油氣運輸管道組網和調度方法主要有最大角度路由選擇算法、不規則三角網組網調度方法、最少跳數路由調度方法等[2-3]，通過優化的路由算法設計，最大化油氣運輸管道的覆蓋范圍和吞吐量，提高管道油氣運輸能力，取得了一定的研究成果。其中，文獻[4]中提出一種剩余能量均衡調度的油氣運輸管道的組網調度模型，采用動態自適應性路由節點定位技術進行管道節點的組網設計，設計均衡控制方法提高油氣運輸管道網絡傳輸的均衡性，但該組網控制方法抗局部干擾能力不強，全局均衡性不好；文獻[5]提出一種基于量化傳感融合跟蹤識別的油氣運輸調度技術，采用無線傳感組網技術進行管道節點的優化部署設計，結合量化分析方法提高管道節點對油氣的自組織收發能力，整個網絡的暢通性較好，但該組網結構復雜，在應對大規模的油氣運輸管道調度時的工程實踐應用性不好。

針對上述問題，本文提出一種基于變結構模糊神經網絡控制的油氣運輸管道調度技術。首先采用三層變結構的PID神經網絡模型進行油氣運輸管道的網絡結構模型，然后采用地理位置尋優算法進行油氣運輸管道組網的最優路由設計，以各個壓氣站為Sink節點進行能量融合均衡調度，建立油氣運輸管道調度的控制目標函數并進行全局穩定性求證，根據模糊神經網絡的積分控制方法進行管道調度的路徑規劃最優解求解，縮短了管道組網路徑，提高管道網絡的吞吐性能和均衡性。最后進行仿真測試，得出有效性結論。

1 油氣運輸管道的網絡結構模型

1.1 三層變結構的PID神經網絡

為了實現對油氣運輸管道調度優化，首先進行網絡組網結構模型分析，采用三層變結構的PID神經網絡模型進行油氣運輸管道的網絡結構模型研究[6]，如圖1所示。

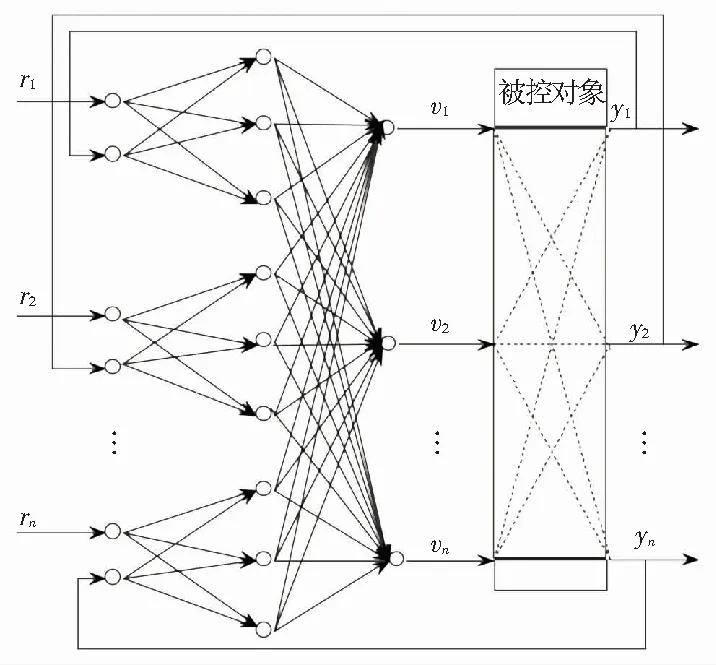
圖1 油氣運輸管道三層變結構的PID神經網絡

Fig.1ThreelayervariablestructurePIDneuralnetworkforoilandgaspipeline

在圖1所示的油氣運輸管道組網PID網絡結構模型中，輸入層有2n個相同的神經元，作為網絡的Source與Sink節點，神經元的輸入為油氣運輸管道的當前負載:

(1)

油氣運輸管道網絡過載邊的神經元狀態為：

usi(k)=netsi(k)

(2)

式(2)表示油氣運輸管道網絡過載邊，輸入層神經元的輸出為：

(3)

表示每個轉運節點的能量消耗和路徑損耗，為了使得整個網絡的路徑消耗最小，選定任意一個結點作為開始結點進行均勻遍歷，給定能量閾值，令管道運輸的失效過載比可表述為：

(4)

當不考慮整個油氣運輸管道調度系統的不確定因素時，通過2×(m0-1)條有向邊連接每個壓氣站節點，得到管道網絡的拓撲控制函數描述為：

(5)

在上述構造的三層變結構的PID神經網絡模型中，采用地理位置尋優算法進行油氣運輸管道組網的最優路由設計，實現管道優化調度。

1.2 地理位置尋優算法

地理位置尋優算法的原理是將運輸管道的遍歷過程看作一個時間離散的馬爾科夫過程[7]，在不同管道鋪設路段中，以管道的流量和阻抗狀態為約束參量，構造管道調度的滑模面，定義為：

s=ce1+e2

(6)

則根據流量模型可以確定管道網絡有向邊的分布特征函數：

(7)

令:

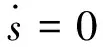
(8)

則得到油氣運輸管道調度的阻抗模型為：

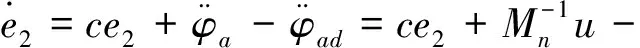
(9)

從已生成的網絡中選擇終端結點，各支路輸出量x1，x2，…，xn分別乘上權重值w1j，w2j，…，wnj，得到油氣運輸管道調度的等效控制律為：

(10)

考慮系統存在不確定因素，在任意時刻t，對模糊神經網絡的第j個神經元進行自學習優選控制，選擇到達律為：

(11)

遍歷管道網絡的結點列表，得到油氣運輸網絡的路由分配函數為：

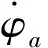
(12)

對上式進行Lyapunove泛函，實現油氣運輸網絡鋪設組網的地理位置自適應尋優，有效降低組網的路徑開銷。

2 油氣運輸管道調度模型優化

2.1 能量融合均衡調度

在上述構建了油氣運輸管道的網絡結構模型的基礎上，進行油氣運輸管道調度算法優化設計，本文提出一種基于變結構模糊神經網絡控制的油氣運輸管道調度技術，以各個壓氣站為Sink節點進行能量融合均衡調度[8]，給出第r輪，節點ni的最優接收油氣流量的輸出函數由f(·)決定，以神經元狀態uj為自變量，得到管道的輸出流量狀態函數為：

xj(k)=f(uj(t))

(13)

這里采用Sigmoid函數作為能量融合的傳導模型，其表達式為：

(14)

采用模糊神經網絡控制方法進行管道節點輸出流量的自適應調節，對于神經網絡的2個Sink神經元，在任意采樣時刻k，其輸入的油氣吞吐量為：

neti(k)=ri(k)i=1,2

(15)

在最優調度策略下，輸入層神經元的油氣流量控制狀態函數為：

(16)

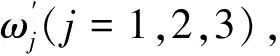
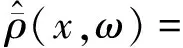
(17)

(18)

2.2 油氣運輸管道調度全局穩定性分析

下面對所設計的油氣運輸管道調度模型的穩定性進行證明分析。

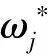
(19)

假設2在全局綜合調度過程中，油氣運輸量和路徑損耗存在不確定控制約束變量的上界滿足：

(20)

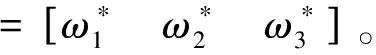
(21)

(22)

定義Lyapunov函數為：

(23)

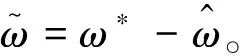
(24)

基于Lyapunove穩定性原理，得到本文設計的基于模糊神經網絡的油氣運輸管道調度模型是全局漸進穩定的，系統的穩定性得證。

3 仿真實驗與性能測試

為了驗證本文設計算法在實現油氣運輸管道優化調度中的應用性能，進行仿真實驗，實驗采用Matlab仿真軟件設計，實驗以1 000 m×1 000 m二維平面作為油氣運輸管道網絡的覆蓋區域，管道的Sink節點數量為100，Source節點數量為12，管道網絡區域分割的網格大小為24 m2，簇頭分布節點數目分別為15,30,30,50,100，在管道中的油氣傳輸速率記為10 Mbps，路由跳數間歇時間為0.2 s，簇首節點的最大覆蓋距離為50 m，神經網絡的級數為24，神經元個數為100，信道衰減常數為12，傳輸能量損失為3.249 77 KJ，根據上述仿真環境和參量設定，進行油氣運輸管道調度仿真，在不同流場下測試不同的調度模型進行油氣運輸管道調度的均衡性，得到結果如圖2所示。

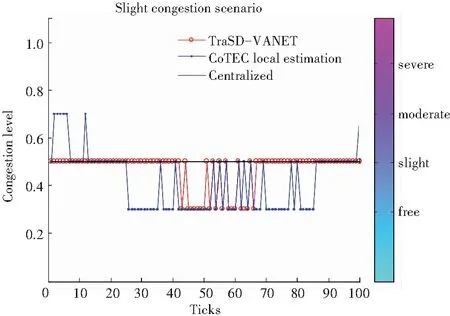
(b)石油流場(b) Oil flow field

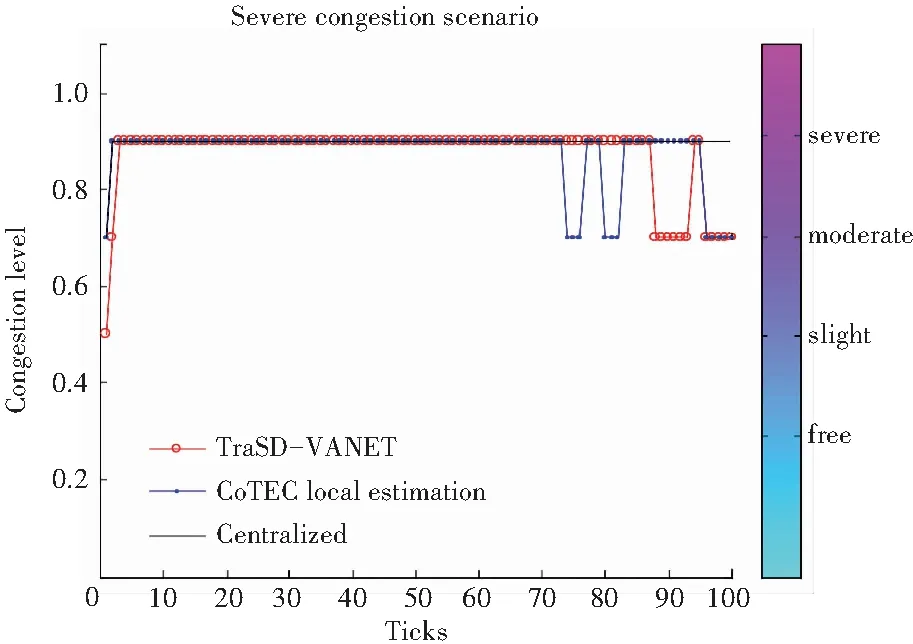
(c)混合流場(c) Mixed flow field圖2 不同流場下不同模型進行調度均衡性對比

Fig.2Comparisonofschedulingequilibriaofdifferentmodelsunderdifferentflowfields

分析圖2結果得知，采用本文模型進行油氣運輸管道調度的均衡性較好，輸出流量分布曲線的平滑性較好，說明管道輸出的全局穩定性較好，最后統計分析得知，本文方法提出的油氣運輸管道調度的吞吐量比傳統方法提高了25.87%，管道鋪設路徑節省12.65%，效能改善顯著。

4 結束語

本文研究一種優化的油氣運輸管道調度技術，提高油氣運輸管道的全局穩定性和暢通性，提出一種基于變結構模糊神經網絡控制的油氣運輸管道調度技術。采用三層變結構的PID神經網絡模型進行油氣運輸管道的網絡結構建模，采用地理位置尋優算法進行油氣運輸管道組網的最優路由設計，進行管道運輸的能量融合均衡調度，并對調度模型進行全局穩定性分析，研究表明，采用本文模型進行油氣運輸管道調度的均衡性較好，縮短了管道組網路徑，提高管道網絡的吞吐量和油氣運輸的平穩性。

[1] 尤冬石,劉亞龍,殷若鵬. 基于定量遞歸分析的天然氣管線輸送流量均衡調度方法[J]. 智能計算機與應用,2016,6(4):16-19.

[2] JIANG Yizhang, CHUNG Fulai, WANG Shitong, et al. Collaborative fuzzy clustering from multiple weighted views[J]. IEEE Transactions on Cybernetics, 2015, 45(4): 688-701.

[3] LONG Mingsheng, WANG Jianmin, DING Guiguang, et al. Adaptation regularization: A general framework for transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(5): 1076-1089.

[4] PATRICIA N, CAPUTO B. Learning to learn, from transfer learning to domain adaptation: A unifying perspective[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH, USA:IEEE, 2014: 1442-1449.

[5] SUN Leilei, GUO Chonghui. Incremental affinity propagation clustering based on message passing[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(11): 2731-2744.

[6] 李可,米捷. 基于變結構PID的仿生機器人機電控制算法[J]. 河南工程學院學報(自然科學版),2016,28(2):32-37.

[7] 崔永君,張永花. 基于特征尺度均衡的Linux系統雙閾值任務調度算法[J]. 計算機科學,2015,42(6):181-184.

[8] 薛明,許德剛. 基于云網格集成調度的防擁堵車輛路徑規劃算法[J]. 計算機科學,2015, 42 (7):295-299.

[9] 龔聰. 改進神經網絡煤礦安全評價模型仿真研究[J]. 計算機仿真,2012,29(1):156-159.

[10]宋明紅,俞華鋒,陳海燕. 改進量子進化算法在計算機網絡路由選擇中的應用研究[J]. 科技通報,2014,30(1):170-173.