基于雙橢圓弧型中弧線的系列翼型設計方法

張 森，席德科，劉治斌，陳寶峰

?

基于雙橢圓弧型中弧線的系列翼型設計方法

張 森1，席德科1※，劉治斌2，陳寶峰2

（1. 西北工業大學航空學院，西安 710072； 2. 山西安瑞風機電氣股份有限公司，運城 044402）

為了能夠方便快捷的設計和修改翼型，采用兩段橢圓弧來構造翼型的中弧線，并推導了描述中弧線的方程式。用該方法構造的中弧線光滑連續，且不存在拐點。選用現有翼型的厚度分布，與中弧線分布函數進行疊加，并引入厚度比例因子來實現對厚度的調整，最終得到了一種基于雙橢圓弧型中弧線的翼型設計方法，稱之為DEA（double ellipse arcs）翼型。選用Clark-Y翼型作為基礎翼型，設計了多款DEA翼型，并利用X-foil軟件對翼型氣動性能進行求解，分別研究了最大相對彎度、最大彎度相對位置、最大相對厚度以及翼型中弧線的形狀因子對翼型氣動性能的影響。研究表明：增加最大相對彎度，可以提高翼型的升力系數，同時使翼型的升阻特性得到一定的改善；最大彎度位置前移，可以提高翼型在小攻角下的升力系數，同時增加翼型高效升阻比的攻角范圍；增加最大相對厚度可以提高翼型的最大升力系數，以及增大失速攻角，同時，高效升阻比的攻角范圍也隨著翼型最大相對厚度的增大而增加；中弧線前、后緣形狀因子對翼型氣動性能的影響相對較小。

設計；翼型；數值分析；中弧線；橢圓弧

0 引 言

翼型作為航空技術發展的產物，被廣泛的應用于流體機械產品的設計中，如壓縮機、軸流風機、軸流泵、風力機等，翼型的氣動特性是決定流體機械性能優劣的一個關鍵因素[1-5]。

當選擇已有的翼型尚不能滿足工程要求時，需要重新設計或者對原有翼型進行修型。目前此項工作主要依靠計算空氣動力學的方法設計，以減少甚至取代翼型風洞試驗，具體實施方法有直接法和逆設計[6-8]。直接法基本過程：首先確定目標，然后人工修改翼型型線或數據，計算氣動特性并與設計要求比較分析，重復進行修正，直到滿足要求，該方法要求設計者有較深厚的專業知識和豐富的設計經驗。逆設計基本過程：給定壓力分布目標函數和約束條件，通過智能優化方法自動修改翼型外形，經過多次迭代，達到收斂條件為止，該方法可以進行多點/多目標的設計，但計算量大，特別是設計變量較多時尤為突出[9-15]。

翼型的型線決定了繞翼型流場特性參數的分布，即翼型的氣動性能，是翼型分析的基礎和關鍵。翼型的型線表達方法主要有：外形參數化方法[16]、形函數擾動法[17]、解析函數法[18-19]。Ray T等[20]采用翼型的特征參數對翼型外形參數化，設計變量幾何意義明確，但未能給出解析表達式。形函數擾動法是由原始翼型和擾動形函數的線性疊加實現[21-22]。解析函數法就是用一個解析函數直接表示翼型形狀，例如早期用多項式表達的NACA的4位數、5位數系列翼型，此外也有研究用級數表達翼型的方法[23]。

Mark[24]于1989年開發了X-foil翼型分析與設計系統，該軟件對于黏性流體采用了面元法和邊界層理論，由于其計算簡單方便，適合于低速翼型的快速分析和設計，因此得到了廣泛應用[25-29]。Ashok G等[30]對比了NLF(1)-0416和NLF(1)-0215F翼型的X-foil計算結果與試驗數據，指出X-foil程序可以用于優化設計中計算不同外型的翼型氣動性能。鄧磊等[31]研究并發展了一套進行高升阻比自然層流翼型多設計點/多設計目標的優化設計方法。為減少設計中的計算量，使用了X-foil程序進行流場計算，進一步驗證了該軟件的可靠性。

本文采用兩段橢圓弧來構造翼型的中弧線，并推導了中弧線的方程式，最終得到了一種基于雙橢圓弧型中弧線的翼型設計方法，利用X-foil軟件分析了翼型幾何特征參數對該系列翼型氣動性能的影響規律，并給出翼型設計指導準則。

1 翼型幾何特征參數

圖1中給出了翼型的幾何特征參數。

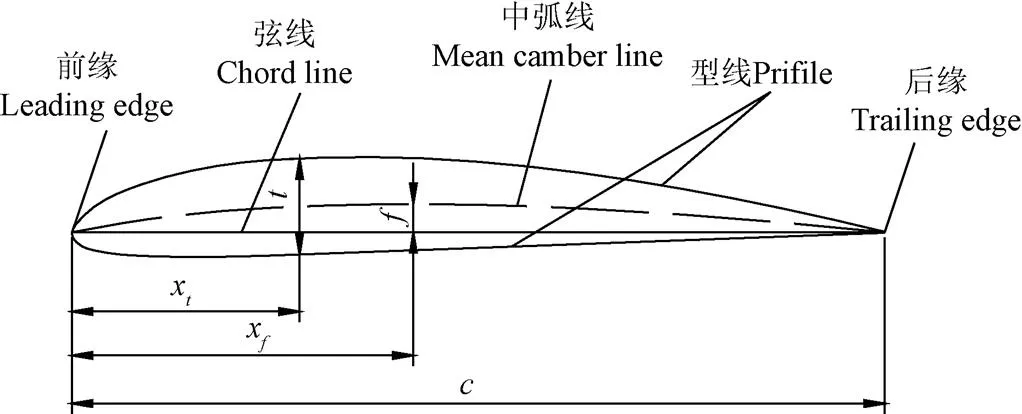
注：c表示翼型的弦長，mm，將c設定為1；t表示翼型的最大相對厚度；f表示翼型的最大相對彎度；xt表示翼型最大厚度相對弦長的位置；xf表示翼型最大彎度相對弦長的位置。

2 雙橢圓弧型中弧線函數的構造

2.1 雙橢圓弧型中弧線函數的求解

采用頂點重合的2個橢圓上截得的橢圓弧來構造翼型中弧線，具體方法如圖2所示，為了方便描述，將翼型的弦長定義為1。

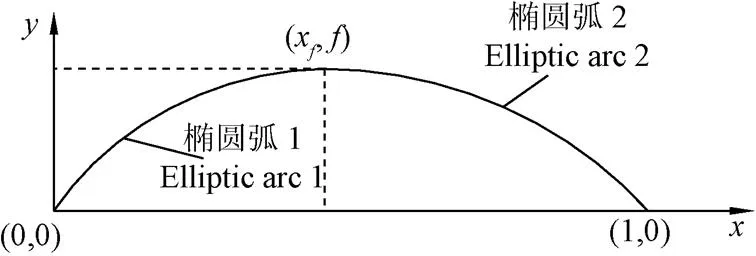
圖2 雙橢圓弧型中弧線示意圖

圖2中，點(0,0)與(1,0)分別為翼型的前緣點和后緣點，點(x,)為橢圓的頂點。中弧線型線方程y如式（1）所示。

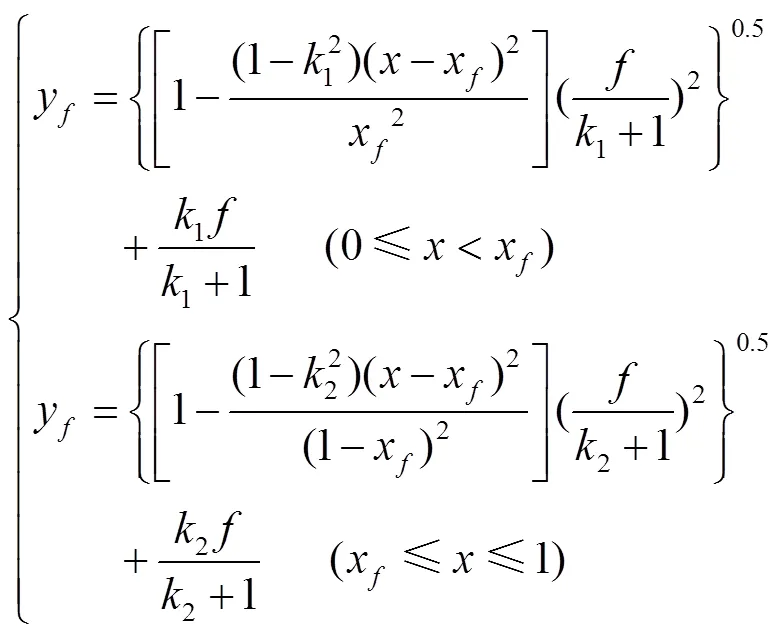
式中1為翼型中弧線前緣形狀因子，?1<1≤0；2為翼型中弧線后緣形狀因子，?1<2≤0。

2.2 中弧線形狀因子k1和k2對中弧線形狀的影響

當翼型中弧線的最大相對彎度和最大彎度相對位置x一定時，通過調整方程（1）中形狀因子1和2的大小可以局部調整中弧線的形狀。

為了研究形狀因子1和2對中弧線形狀的影響，在圖3中給出了最大相對彎度=3.43%，最大彎度相對位置x=40%時，中弧線前緣形狀因子1=?0.99，中弧線后緣形狀因子2分別為0、?0.2、?0.5、?0.7、?0.99，和中弧線后緣形狀因子2=?0.99，中弧線前緣形狀因子1分別為0、?0.2、?0.5、?0.7、?0.99時的型線圖。

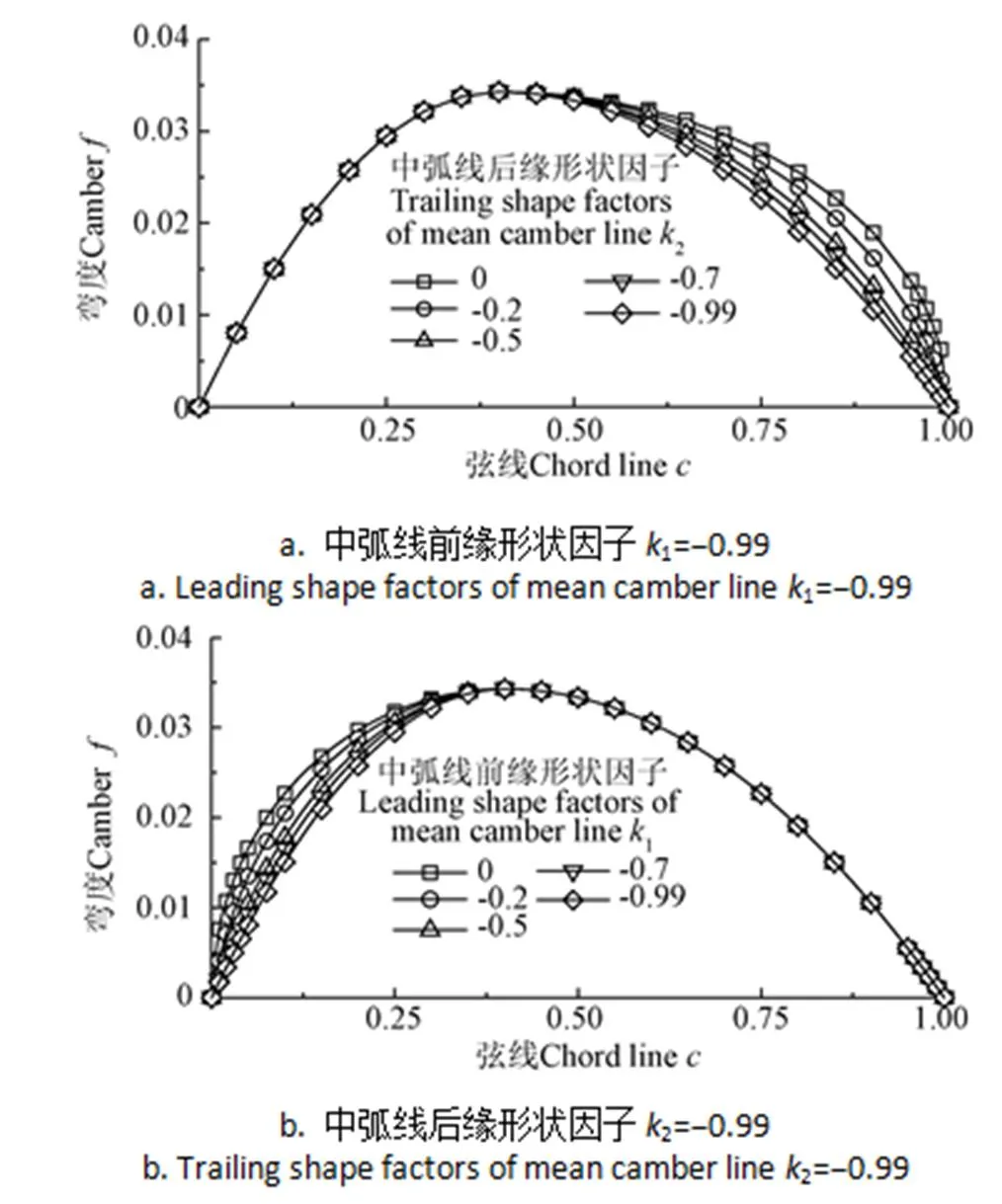
圖3 不同k1和k2時的中弧線型線

由圖3可知，當中弧線前緣形狀因子一定而中弧線后緣形狀因子變化時，前緣點至最大彎度處翼型中弧線型線保持不變，翼型后緣氣流出口角隨著中弧線后緣形狀因子的增大而增大，當中弧線后緣形狀因子2=0時，達到最大值。同樣，當中弧線后緣形狀因子一定而中弧線前緣形狀因子變化時，最大彎度至后緣點翼型中弧線型線保持不變，翼型前緣氣流出口角隨著中弧線前緣形狀因子的增大而增大，當中弧線前緣形狀因子1=0時，達到最大值。結果表明，當中弧線的最大相對彎度和最大彎度相對位置一定時，隨著形狀因子1與2增大，翼型中弧線型線變得飽滿，對應的氣流角也逐漸增大，且形狀因子1與2對型線的影響以最大彎度位置為分界點，相互獨立。

3 系列翼型設計方法

翼型的型面函數可以表示為中弧線分布函數與厚度分布函數的疊加，如式（2）所示。

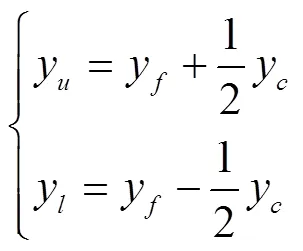
式中y、y分別表示翼型的上表面型面函數和下表面型面函數；y表示翼型的厚度分布函數。

式（2）中的中弧線分布函數y使用本文推導的式（1），厚度分布函數則選用現有翼型的厚度分布。為了能夠調節翼型最大相對厚度的大小，引入了厚度比例因子，其表達式為

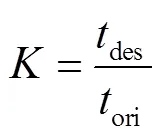
式中des表示設計翼型的最大相對厚度；ori表示原始翼型的最大相對厚度。

因此，可根據實際需要，通過調整厚度比例因子的大小得到理想的最大相對厚度。在式（2）的厚度項y前乘以系數，得到

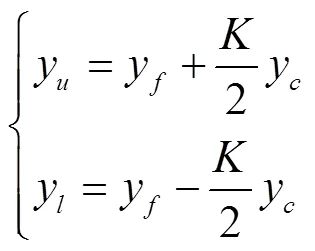
式（4）給出了最終的翼型型面函數表達式。本文將該方法構造的翼型稱之為DEA（double ellipse arcs）翼型。

4 結果與分析

選用Clark-Y翼型作為基礎翼型，運用上述DEA翼型設計方法進行翼型設計。Clark-Y翼型的幾何特征參數如下：最大相對厚度=11.71%，最大厚度相對位置x=28%，最大相對彎度=3.43%，最大彎度相對位置x=42%。在與Clark-Y翼型具有相同幾何特征參數的條件下，取中弧線形狀因子1=?0.8，2=?0.99，設計了一款DEA翼型，如圖4所示。

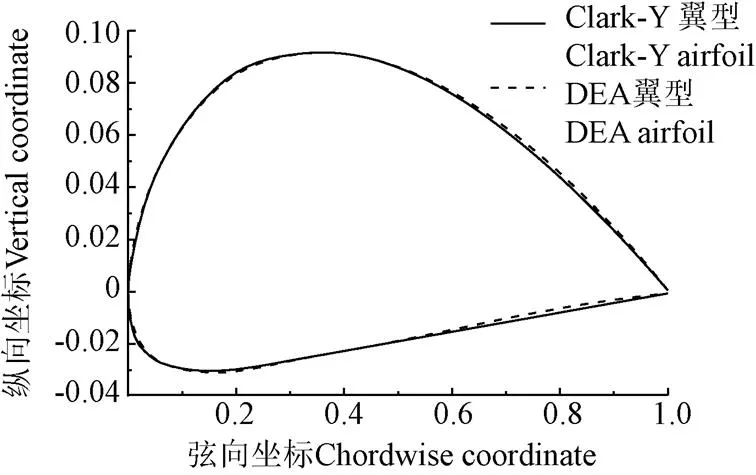
圖4 Clark-Y翼型與DEA翼型的型線對比

Clark-Y翼型與DEA翼型的型線對比結果顯示，兩者的型線有較好的重合度，采用DEA翼型設計方法能夠便捷的對現有翼型進行參數化。

為了研究幾何特征參數對DEA翼型氣動性能的影響，本文利用X-foil軟件對翼型氣動性能進行求解，取雷諾數=1.0×105。

4.1 最大相對彎度f對DEA翼型氣動性能的影響

在最大相對厚度=11.71%、最大厚度相對位置x=28%和最大彎度相對位置x=42%的情況下，取中弧線形狀因子1=?0.8，2=?0.99，分別設計了最大相對彎度為3.42%、4%、5%、6%時的翼型，氣動性能計算結果如圖5所示。

由圖5可看出，在最大相對厚度、最大厚度相對位置和最大彎度相對位置相同的情況下，基礎翼型Clark-Y與最大相對彎度=3.43%時的DEA翼型的性能曲線有較高的重合度，這里進一步驗證了用DEA翼型參數化設計方法設計翼型的可靠性。當只改變最大相對彎度時，翼型的升力系數曲線在小攻角范圍內基本保持平行，在同一攻角下，隨著最大相對彎度的增大，升力系數也隨之增大。此外，隨著最大相對彎度的增大，翼型的升阻比曲線也發生了變化，當最大相對彎度=6%時，在0°、6°和12°攻角處，翼型的升阻比相對于Clark-Y翼型分別提高了6.88%、1.59%和24.49%。研究表明，在翼型厚度、最大厚度位置和最大彎度位置不變的情況下，增大相對彎度，可以提高DEA翼型的升力系數，同時使翼型的升阻特性得到一定的改善。

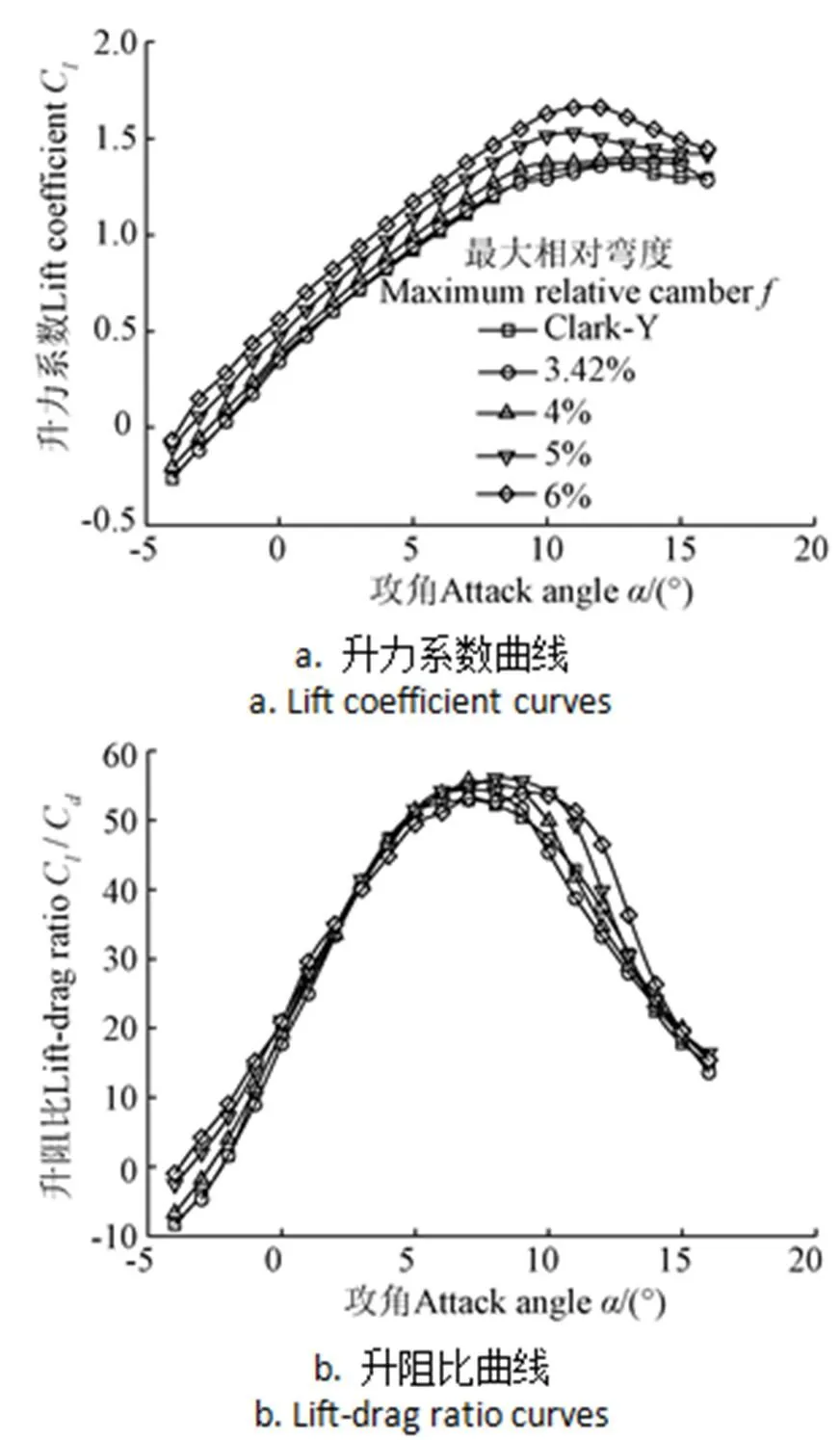
注：表示翼型攻角，(o)；Cl表示翼型的升力系數；Cd表示翼型的阻力系數；Cl/Cd表示翼型的升阻比。

4.2 最大彎度相對位置xf對DEA翼型氣動性能的影響

為了研究最大彎度相對位置x對DEA翼型氣動特性的影響，在最大相對厚度=11.71%、最大厚度相對位置x=28%和最大相對彎度=3.43%的條件下，取中弧線形狀因子1=?0.8，2=?0.99，分別設計了最大彎度相對位置x為25%、42%、50%、60%時的翼型，并對其氣動性能進行了計算，計算結果如圖6所示。

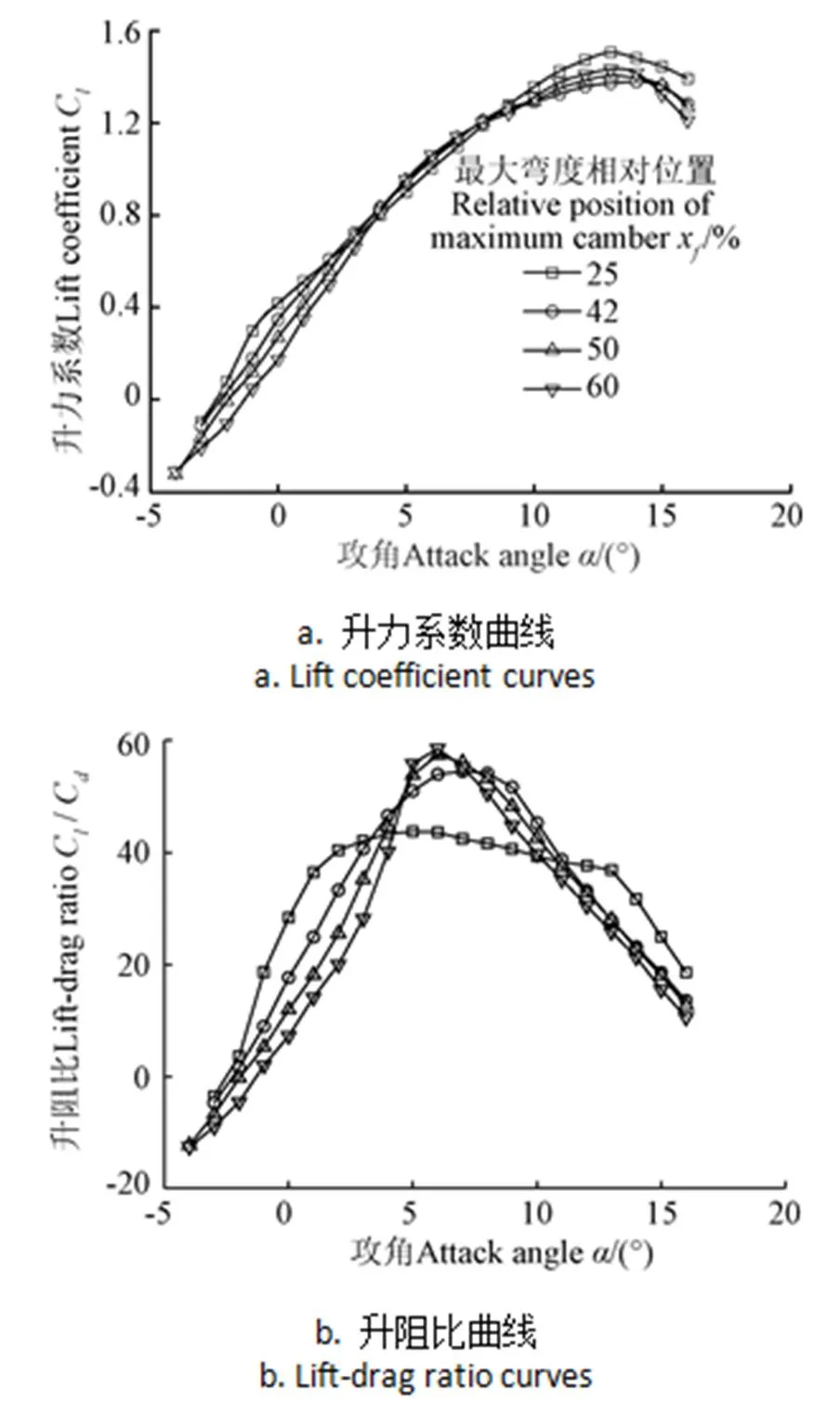
圖6 不同xf下的DEA翼型氣動性能曲線

4.3 最大相對厚度t對DEA翼型氣動性能的影響

由薄翼理論可知，對于理想不可壓縮流體的翼型繞流，如果氣流繞翼型的迎角、翼型厚度、翼型彎度都很小，則繞流場是一個小擾動的勢流場。這時，翼面上的邊界條件和壓強系數可以線性化為厚度、彎度、迎角三者影響的疊加。因此翼型的厚度對氣動性能也起到至關重要的影響。圖7中給出了最大彎度相對位置x=25%、最大厚度相對位置x=28%、最大相對彎度=3.43%，最大相對厚度分別為6%、8%、10%和11.71%時的DEA翼型氣動特性曲線，中弧線形狀因子取1=?0.8，2=?0.99。

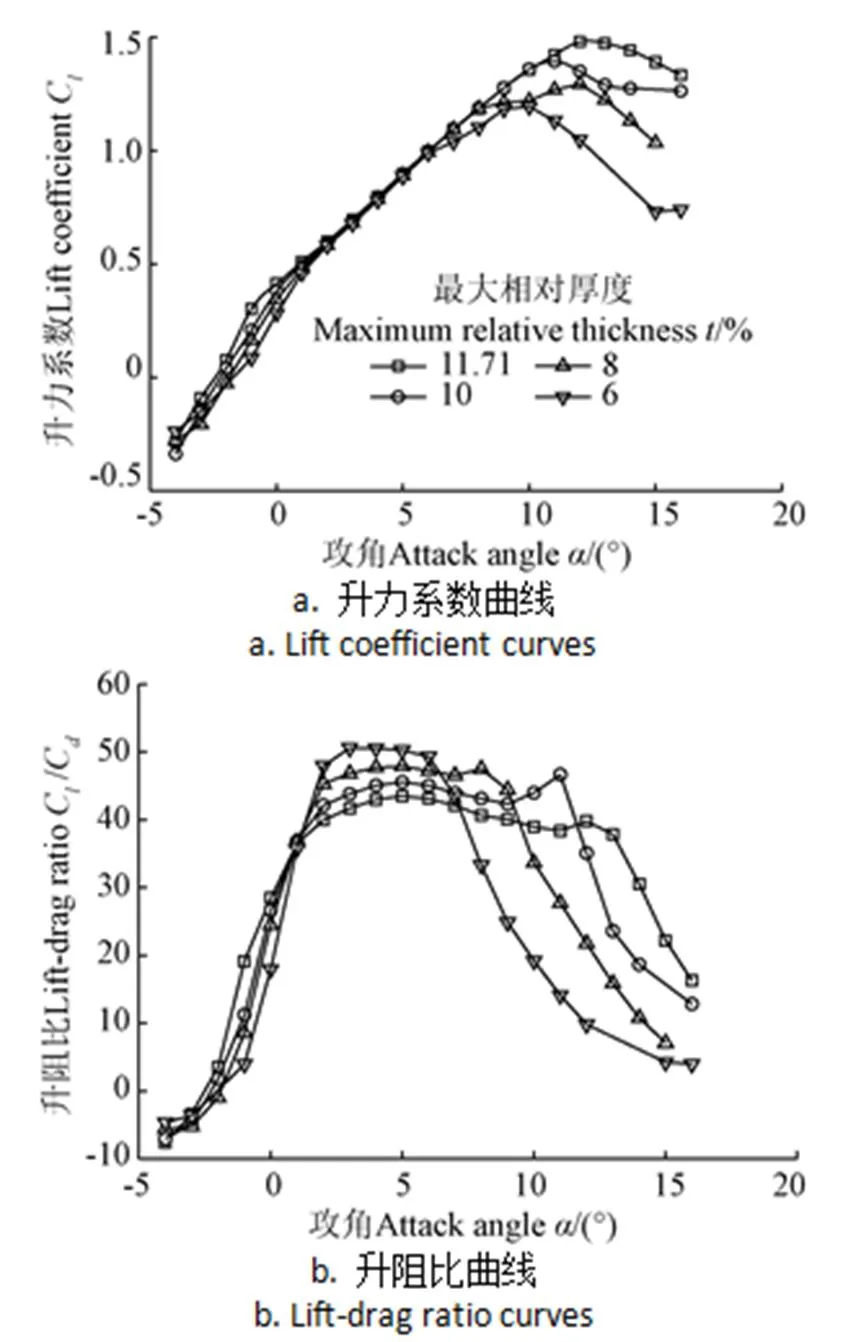
圖7 不同t下的DEA翼型氣動性能曲線

4.4 中弧線形狀因子k1與k2對DEA翼型氣動性能的影響

為了研究中弧線形狀因子1和2對DEA翼型氣動特性的影響，分別設計了最大相對厚度=11.71%、最大彎度相對位置x=42%、最大厚度相對位置x=28%、最大相對彎度=3.43%時，中弧線形狀因子1=?0.2、?0.5、?0.7、?0.99，2=?0.99和1=?0.99，2=?0.2、?0.5、?0.7、?0.99的翼型，性能計算結果如圖8和圖9所示。

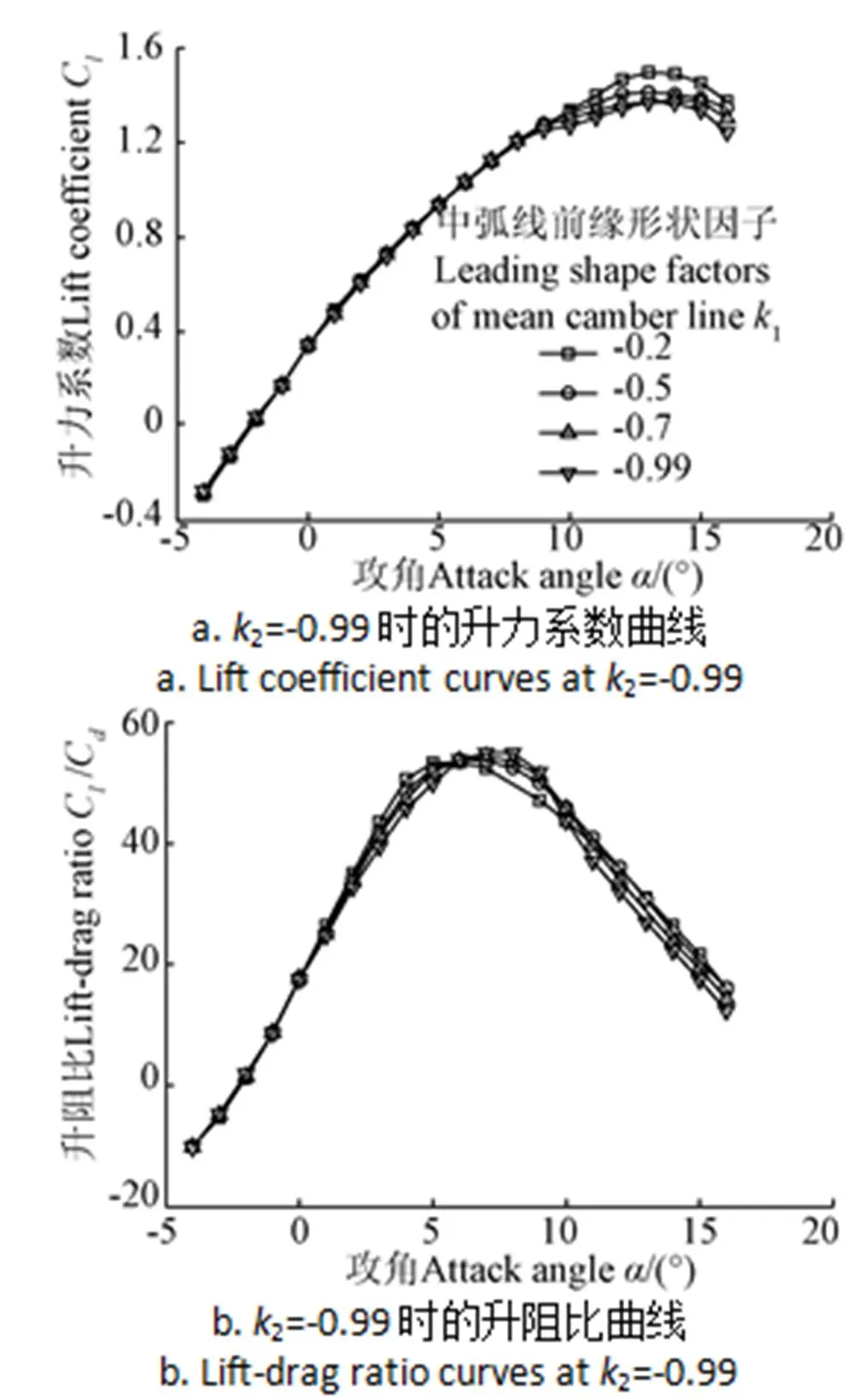
圖8 不同k1下的DEA翼型氣動性能曲線

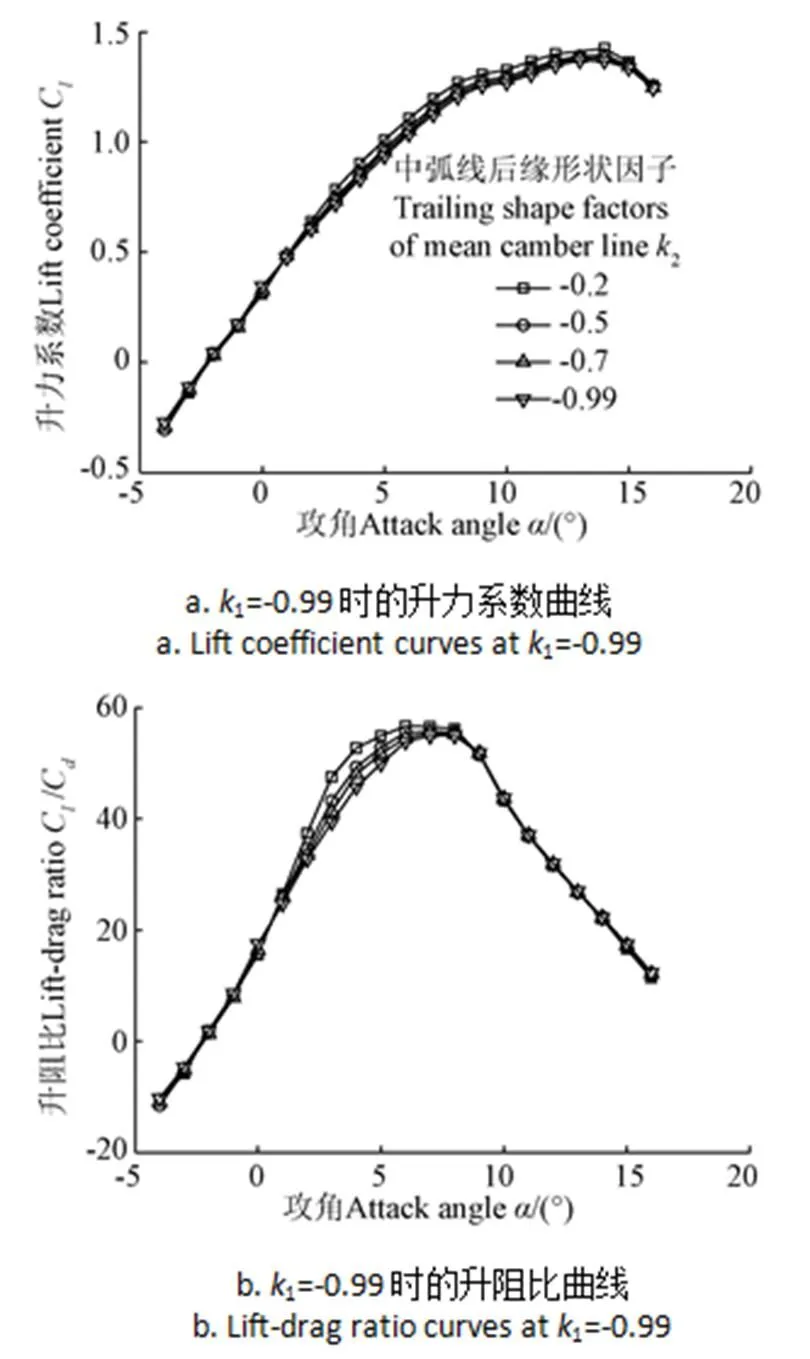
圖9 不同k2下的DEA翼型氣動性能曲線

5 結 論

1）采用兩段橢圓弧來構造翼型中弧線，并推導了中弧線方程式，該方程通過改變最大彎度和最大彎度相對位置對中弧線形狀進行控制，并由翼型中弧線形狀因子實現局部微調。用該方法構造的中弧線光滑連續，且不存在拐點。

2）選用現有翼型的厚度分布，與中弧線分布函數進行疊加，并引入厚度比例因子來實現對厚度的控制，最終得到了一種基于雙橢圓弧中弧線的翼型設計方法，本文將該方法構造的翼型稱之為DEA（double ellipse arcs）翼型。

3）選用Clark-Y翼型作為基礎翼型，設計了多款DEA翼型，并利用X-foil軟件對翼型氣動性能進行求解，分別研究了最大相對彎度、最大彎度相對位置、最大相對厚度，以及翼型中弧線的形狀因子對翼型氣動性能的影響。研究表明：增加最大相對彎度，可以提高翼型的升力系數，同時使翼型的升阻特性得到一定的改善；最大彎度位置前移，可以提高翼型在小攻角下的升力系數，同時增加翼型高效升阻比的攻角區間，但最優升阻比會逐漸減小；增加最大相對厚度可以提高翼型的最大升力系數，以及增大失速攻角，同時，高效升阻比的攻角區間也隨著翼型厚度的增大而增加，但最優升阻比會逐漸減小；中弧線形狀因子對翼型氣動性能的影響較小。

依據上述參數的調整變化原則，可設計出新的翼型或者對原翼型進行修型以滿足目標任務的需要。

[1] Mojtaba Tahani, Ghazale Kavari, Mehran Masdari, et al. Aerodynamic design of horizontal axis wind turbine with innovative local linearization of chord and twist distributions[J]. Energy, 2017, 131: 78－91.

[2] 項松，王吉，張利國，等. 一種高效率螺旋槳設計方法[J]. 航空動力學報，2015，30(1)：136－141.

Xiang Song, Wang Ji, Zhang Liguo, et al. A design method for high efficiency propeller[J]. Journal of Aerospace Power, 2015, 30(1): 136－141. (in Chinese with English abstract)

[3] 沙毅，侯麗艷. 葉片厚度對軸流泵性能影響及內部流場分析[J]. 農業工程學報，2012，28(18)：75－81.

Sha Yi, Hou Liyan. Effects of blade thickness on performance of axial flow pump and analysis of internal flow field[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(18): 75－81. (in Chinese with English abstract)

[4] 汪泉，陳進，王君，等. 基于連續攻角的風力機翼型整體氣動性能提高的優化設計[J]. 機械工程學報，2017，53(13)：143－149.

Wang Quan, Chen Jin, Wang Jun, et al. Wind turbine airfoil optimal design with high whole aerodynamic performance considering continuous angle of attack[J]. Journal of Mechanical Engineering, 2017, 53(13): 143—149. (in Chinese with English abstract)

[5] 徐浩然，楊華，劉超. 尾緣加厚的DU系列翼型氣動性能數值分析[J]. 農業工程學報，2014，30(17)：101－108.

Xu Haoran, Yang Hua, Liu Chao. Numerical value analysis on aerodynamic performance of DU series airfoils with thickened trailing edge[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(17): 101—108. (in Chinese with English abstract)

[6] Srilatha K R, Dwarakanath G S. Design of a natural laminar flow airfoil for a light aircraft[J]. Journal of Aircraft, 1990, 27(11): 966－968.

[7] 王驥月，叢茜，梁寧，等. 基于海鷗翼型的小型風力機葉片仿生設計與試驗[J]. 農業工程學報，2015，31(10)：72－77.

Wang Jiyue, Cong Qian, Liang Ning, et al. Bionic design and test of small-sized wind turbine blade based on seagull airfoil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(10): 72—77. (in Chinese with English abstract)

[8] Green B E. An Approach to the Constrained Design of Natural Laminar flow Airfoils[M]. NASA Langley Technical Report Server, 1997.

[9] 嚴敬，劉小兵，周緒成，等. 基于奇點分布法的軸流泵葉片翼型設計與計算[J]. 農業工程學報，2016，32(7)：100－105.

Yan Jing, Liu Xiaobing, Zhou Xucheng, et al. Design and calculation of airfoil profile of blade in axial flow pump based on singularity approach[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(7): 100－105. (in Chinese with English abstract)

[10] 龍騰，劉莉，孟令濤，等. 基于代理模型的翼型多目標集成優化設計[J]. 系統仿真學報，2010，22(7)：1604－1608.

Long Teng, Liu Li, Meng Lingtao, et al. Multi-objective integrated optimization of airfoil based on surrogate model[J]. Journal of System Simulation, 2010, 22(7): 1604－1608. (in Chinese with English abstract)

[11] Lee J D, Jameson A. Natural-laminar flow airfoil and wing design by adjoint method and automatic transition prediction [C]// 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, Florida, 2009.

[12] Youngren H. Multi-Point design and optimization of an natural laminar flow airfoil for a mission adaptive compliant wing[C]// AIAA Aerospace Sciences Meeting and Exhibit. 2008:485601-485605(5).

[13] Driver J, Zingg D W. Optimized natural-laminar flow airfoils, AIAA-2006-247[R]. Toronto: American Institute of Aeronautics and Astronautics, 2006.

[14] Ashok G, Michael S S. Low speed NLF airfoils: Case study in inverse airfoil design[J]. Journal of Aircraft, 2001, 38(2): 57－63.

[15] 朱國俊，馮建軍，郭鵬程，等. 基于徑向基神經網絡-遺傳算法的海流能水輪機葉片翼型優化[J]. 農業工程學報，2014，30(8)：65－73.

Zhu Guojun, Feng Jianjun, Guo Pengcheng, et al. Optimization of hydrofoil for marine current turbine based on radial basis function neural network and genetic algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(8): 65－73. (in Chinese with English abstract)

[16] Liang Xiao, Meng Guanglei, Tong Shengxi, et al. Rapid design and optimization of airfoil based on improved genetic algorithm[J]. Acta Aerodynamica Sinica, 2016, 31(6): 803－812.

[17] 王迅，蔡晉生，屈崑，等. 基于改進CST參數化方法和轉捩模型的翼型優化設計[J]. 航空學報，2015，36(2)：449－461.

Wang Xun, Cai Jinsheng, Qu Kun, et al. Airfoil optimization based on improved CST parametric method and transition model[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 449－461. (in Chinese with English abstract)

[18] 姜海波，趙云鵬. 基于中弧線—厚度函數的翼型形狀解析構造法[J]. 圖學學報，2013，34(1)：50－54.

Jiang Haibo, Zhao Yunpeng. Analytic expression method of airfoil profile shape based on a mean camber and thickness function[J]. Journal of Graphics, 2013, 34(1): 50－54. (in Chinese with English abstract)

[19] 姜海波，程忠慶，趙云鵬. 翼型型線的參數表達式探討[J]. 機械設計與制造，2015，3：69－72.

Jiang Haibo, Cheng Zhongqing, Zhao Yunpeng. Study on parameter expressions of airfoil contour[J]. Machinery Design and Manufacture, 2015, 3: 69－72. (in Chinese with English abstract)

[20] Ray T, Tsai H M. Swarm algorithm for single and multiobjective airfoil design optimization[J]. AIAA Journal, 2004, 42(2): 366－373.

[21] David W Z, Timothy M L, Laslo D, et al. Improvements to a newton-krylov adjoint algorithm for aerodynamic optimization, AIAA-2005-4857[R]. Toronto: American Institute of Aeronautics and Astronautics, 2005.

[22] 劉周，朱自強，付鴻雁，等. 高升阻比翼型的設計[J]. 空氣動力學學報，2004，22(4)：410－415.

Liu Zhou，Zhu Ziqiang，Fu Hongyan，et al. Design of airfoil with high ratio of lift over drag[J]. Acta Aerodynamica Sinica, 2004, 22(4): 410－415. (in Chinese with English abstract)

[23] 陳進，張石強，Eecen P J，等. 風力機翼型參數化表達及收斂特性[J]. 機械工程學報，2010，46(10)：132－138.

Chen Jin, Zhang Shiqiang, Eecen P J, et al. Parametric representation and convergence of wind turbine airfoils[J]. Journal of Mechanical Engineering, 2010, 46(10): 132－138. (in Chinese with English abstract)

[24] Mark D. XFOIL: An analysis and design system for low reynolds number airfoils[J]. Lecture Notes in Engineering, 1989, 54: 1－12.

[25] Bangga G, Hutomo G, Wiranegara R, et al. Numerical study on a single bladed vertical axis wind turbine under dynamic stall[J]. Journal of Mechanical Science and Technology, 2017, 31(1): 261－267.

[26] Ananda G K, Sukumar P P, Selig M S. Measured aerodynamic characteristics of wings at low Reynolds numbers[J]. Aerospace Science & Technology, 2015, 42: 392－406.

[27] Morgado J, Vizinho R, Silvestre M A R, et al. XFOIL vs CFD performance predictions for high lift low Reynolds number airfoils[J]. Aerospace Science and Technology, 2016, 52: 207－214.

[28] Ramanujam G, ?zdemir H, Hoeijmakers H W M. Improving airfoil drag prediction[C]//Wind Energy Symposium, AIAA Scitech. 2016.

[29] Paulo A S F S, Léo D S, Taygoara F O, et al. Analysis of cavitation for the optimized design of hydrokinetic turbines using BEM[J]. Applied Energy, 2017, 185: 1281－1291.

[30] Ashok G, Michael S S. Low-speed natural-laminar-flow airfoils: case study in inverse airfoil design[J]. Journal of Aircraft, 2001, 38(1): 57－63.

[31] 鄧磊，喬志德，楊旭東，等. 高升阻比自然層流翼型多點/多目標優化設計[J]. 空氣動力學學報，2011，29(3)：330－335.

Deng Lei, Qiao Zhide, Yang Xudong, et al. Multi-point/ objective optimization design of high lift-to-drag ratio for NLF airfoils[J]. Acta Aerodynamica Sinica, 2011, 29(3): 330－335. (in Chinese with English abstract)

Design method for series airfoil based on mean camber line consisting of double ellipse arcs

Zhang Sen, Xi Deke, Liu Zhibin, Chen Baofeng

Institute of Aeronautics, Northwestern Polytechnical University, Xi’an, ChinaShanxi Anrui Fan Electric Co., Ltd, Yuncheng, China

Airfoil, as a product of aviation technology, has been widely used in the design of fluid machinery products. The aerodynamic characteristics of airfoils are a key factor in determining the performance of fluid machinery. When the existing airfoils are not able to meet the engineering requirements, it is necessary to redesign or trim the original airfoils. In this research, 2 ellipse arcs were used to form the mean camber line of the airfoil, and the corresponding equation was deduced. This equation controls the shape of the mean camber line by changing the maximum camber and the relative position of maximum camber, and adjusts the local shape by changing the 2 shape factors of the mean camber line. The mean camber line constructed by this method is smooth and continuous, and there is no knee point. Then the thickness distribution of the existing airfoil was superposed with the distribution function of mean camber line, and a thickness scale factor was introduced to adjust the thickness distribution. Ultimately, the design method for a series of airfoils based on mean camber line of double ellipse arcs is achieved, which is called DEA (double ellipse arcs) airfoil. The airfoil profile function constructed by this method has definite physical meaning, simple and reliable, and it is easy to realize serialization. In order to study the influence of airfoil characteristic parameters on aerodynamic performance of the DEA airfoil, the Clark-Y airfoil was taken as the basic airfoil, and a number of DEA airfoils were designed using the thickness distribution of the Clark-Y airfoil. Then the aerodynamic characteristics of the designed airfoils were solved by the X-foil software to study the influence of the maximum camber, the relative position of the maximum camber, the maximum thickness and the shape factors of the mean camber line on the DEA airfoil aerodynamic performance. There are 5 characteristic parameters in all that influence the shape of the DEA airfoil. We selected one of the 5 characteristic parameters as variable and fixed the other 4 characteristic parameters to design different DEA airfoils. And the aerodynamic characteristics were achieved at Reynolds number of 1.0×105. The calculation results of the 4 DEA airfoils with different values of maximum camber show that the increase of the maximum camber can improve the lift coefficient and ameliorate the characteristics of the lift-drag ratio. The calculation results of the 4 DEA airfoils with different values of relative position of the maximum camber show that as the relative position of the maximum camber moves forward, the lift coefficient under small angles of attack is improved, and the range of efficient lift-drag ratio gets broadened. The calculation results of the 4 DEA airfoils with different values of maximum thickness show that the increase of the maximum thickness can increase the maximum lift coefficient and the stall angle. At the same time, with the increase of thickness, the range of efficient lift-drag ratio also gets broadened. The calculation results of the DEA airfoils with different shape factors of the mean camber line also were achieved. At small attack angle, the change of the leading shape factors of the mean camber line has little influence on lift coefficient. With the decrease of the leading shape factors of the mean camber line, the interval of efficient lift-drag ratio has a tendency to move to high attack angle range. With the decrease of the trailing shape factors of the mean camber line, the lift coefficient and lift-drag ratio decrease gradually. Moreover, the interval of efficient lift-drag ratio also decreases and the decrease is mainly at the range of small attack angle. According to the adjustment principle of the above parameters, a new airfoil can be designed or modified to meet the needs of the target task.

design; airfoils; numerical analysis; mean camber line; double ellipse arcs

10.11975/j.issn.1002-6819.2018.02.006

TB126/TB21

A

1002-6819(2018)-02-0040-07

2017-07-07

2017-12-12

國家自然科學基金（11172243）；陜西省科技統籌創新工程計劃（2011KTCQ01-02）

張 森，河南新鄉人，博士生，研究方向為航空高科技軍轉民技術及流體機械設計。Email：sen96@mail.nwpu.edu.cn

席德科，教授，博士生導師，研究方向為風洞設計及流體機械設計。Email：xideke@nwpu.edu.cn

張 森，席德科，劉治斌，陳寶峰. 基于雙橢圓弧型中弧線的系列翼型設計方法[J]. 農業工程學報，2018，34(2)：40－46. doi：10.11975/j.issn.1002-6819.2018.02.006 http://www.tcsae.org

Zhang Sen, Xi Deke, Liu Zhibin, Chen Baofeng. Design method for series airfoil based on mean camber line consisting of double ellipse arcs[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(2): 40－46. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.02.006 http://www.tcsae.org