基于風向預測的偏航控制策略研究

文 | 路宏，田德，龐輝慶，吳志學，王若愚

風能是可再生能源，具有蘊含量大、分布廣泛、綠色無污染等諸多優點，其開發利用在世界范圍內得到了廣泛的重視。偏航系統是風電機組實現快速有效對風，提高風能利用率的重要執行機構，是水平軸風電機組不可或缺的關鍵部件。由于風的隨機性，風電機組根據采集的風向數據執行偏航時會產生偏航滯后、引起偏航誤差，進而導致風能利用率降低，并且使機組所受的不對稱載荷增加。因此，偏航系統性能直接決定風電機組的經濟性和安全性。

為提高風電機組的對風精度，提升風電機組偏航系統的工作效率，提高系統穩定性、可靠性及經濟性，研究者們提出了多種偏航控制策略。其中代表性的研究成果有：基于爬山法（HC）的偏航控制策略（其中包含風向標控制與爬山法相結合的基于V-HC算法的偏航控制策略以及結合卡爾曼濾波算法的基于K-HC算法的偏航控制策略）、基于CPSO算法的PIDNN偏航控制策略、基于模糊算法與傳統PID控制相結合的偏航控制策略以及基于人工神經內分泌免疫調節的偏航控制策略等。以上偏航控制策略主要根據歷史風向控制偏航系統，并未結合風向變化趨勢，無法保證機組偏航結束后的對風精度。隨著預測算法的逐步完善，有研究者結合風向預測提出了基于BP神經網絡風向預測的偏航控制策略、基于時間序列預測與卡爾曼濾波結合的風向預測的偏航控制策略，以及基于聚類算法和風向預測的偏航控制優化策略。這些基于風向預測的偏航控制策略以預測風向代替實際風向作為偏航系統的輸入，雖然提高了對風精度，但會增加偏航系統重啟次數。

基于此，本文提出一種基于時間序列模型預測的偏航控制策略。為避免偏航控制系統頻繁重啟，該策略仍采用傳統的偏航啟動策略，并且根據預測的平均風向執行偏航系統控制。仿真結果表明該偏航控制策略可在減少機組偏航動作次數的同時，提高對風精度。

偏航系統工作原理

偏航系統是一種對風裝置，一般由偏航驅動裝置、偏航傳動裝置、偏航計數器、偏航制動器、風速風向儀、偏航軸承、扭纜保護裝置等組成。

風電機組通過風向風速儀檢測風信號，將測得的信號傳輸到偏航控制器進行數據處理，控制器經過比較判斷后發送偏航命令至偏航執行機構，從而調整機艙位置實現對風。完成對風動作后，偏航電機停止工作，偏航制動器鎖緊，偏航結束。偏航工作原理流程如圖1所示。

圖1 偏航系統工作原理

圖2 傳統偏航控制原理

大型風電機組的偏航控制主要根據傳感器采集的風向信號和已設定的控制邏輯進行偏航。當檢測到過去一段時間內平均風向與當前機艙位置角的差值超過設定角度時，機組開始執行自動偏航實現精準對風。在傳統偏航控制策略下，機組重啟偏航的次數與采集平均風向時間及偏航容許誤差角度有關，提高對風精度會引起機組頻繁偏航動作。傳統偏航控制流程如圖2所示。

其中，θave為上一時刻的平均風向，θp為當前機艙位置，C為偏航容許誤差。

風向預測

風向是時刻變化的，具有很強的波動性和不確定性，而偏航系統作為一種基于風向變化的隨動系統在對風時存在一定的滯后性，為解決偏航滯后的問題，本文提出了一種基于平均風向預測的偏航控制策略。

預測模型是預測的核心，它的建立主要分為傳統統計學方法和人工神經網絡法兩大類。時間序列分析建模是統計學建立預測模型方法中的一種能建立一個反映該序列隨時間變化的模型。由于該模型簡單，建模時間短，可根據有限的樣本序列建立高精度預測模型，符合風向時刻變化的特性，適用于短期內的風向預測，偏航系統可結合預測風向確定偏航角度實現快速響應。基于此，本文選擇一種時間序列分析模型——ARIMA模型作為預測模型。

一、ARIMA模型建模

ARIMA模型又稱自回歸求和移動平均模型，是由自回歸模型（AR）與滑動平均模型（MA）組成。其建模的基本思想是使用差分法對非平穩時間序列進行平穩化處理，通過觀察相關函數截尾和拖尾特征自回歸階數p、差分階數d和移動平均階數q 三個參數，根據最小AIC準則選取AIC最小值確定p、q值建立ARIMA模型，進而對時間序列進行預測分析。ARIMA模型結構如下：

式中，yt代表t時刻的風向預測值，φi代表第i個自回歸系數，θj表示第j個滑動平均系數，ut為獨立的誤差項。

（一）自相關函數與偏自相關函數

在需要對一個時間序列建模時，應用序列的自相關與偏自相關對序列適合的模型類型進行識別，確定適宜的階數p、d、q。

1. 樣本自相關函數

式中，γk是自協方差函數，表達式如下：

式中，σ2＝D（ut），是白噪聲序列的方差。

2. 樣本偏自相關函數

偏自相關是指對于時間序列yt與yt-k之間的條件相關關系，其相關程度由偏自相關系數φkk度量。

式中，γk是滯后k期的自相關系數，

（二）AIC準則定階

AIC準則定階是指在（p,q）的一定變化范圍內尋求使得AIC（S）最小的點（）作為（p,q）的估計。

二、預測實例

選取某風電場2018年5月20日某臺機組的1704個風向數據采樣點284分鐘的風向數據作為研究對象，并選取每4分鐘風向平均值共70個作為第一組時間序列建模的平均風向采樣點，在Matlab中編寫基于時間序列模型預測程序。通過對各采樣點序列相關分析，確定差分次數，根據最小AIC準則選取AIC最小值確定p、q值并建立ARIMA模型，最終選取模型ARIMA（1,0,3）為最優模型（如圖3）。

由圖3可以看出，此預測模型能夠準確預測平均風向的變化趨勢，誤差范圍小，精度較高，可將預測的平均風向值作為偏航執行控制參數。

偏航控制系統優化與驗證

一、改進偏航控制系統

圖3 模型ARIMA（1,0,3）風向預測

圖4 改進偏航控制策略原理

圖5 改進偏航系統控制流程

圖6 機艙位置對比

傳統風電機組偏航控制系統是隨動系統，控制器根據風向與機艙位置的誤差角調整機艙位置。當風向波動頻繁時，機艙位置的調節不僅存在滯后性，還會因頻繁偏航造成嚴重機械磨損。

為解決此類問題，改進偏航控制策略如圖4、圖5所示。

二、仿真驗證及分析

選取某風電場2018年5月20日24小時風向數據作為研究對象，對改進的偏航控制系統進行Matlab仿真驗證。改進的偏航控制策略選取時間段0:00－6:45歷史風向數據進行建模，在6:45－23:59內根據預測的平均風向執行偏航。對比結果如圖6所示。

圖6表明，當風向波動較大時，傳統偏航策略控制的風電機組偏航系統頻繁重啟，其原因在于偏航系統不能根據風向變化趨勢調節機艙位置導致偏航滯后。而應用改進的新型偏航控制策略后機組偏航重啟次數大幅減少，說明其更能滿足對風需求。

圖7為傳統偏航控制和改進的新型偏航控制下的偏航誤差對比圖，傳統偏航控制策略下的偏航誤差波動性更強，新型偏航控制策略下的偏航誤差整體上小于傳統偏航控制策略下的偏航誤差，對風精度更高。根據機艙位置與實際風向數據，得出偏航誤差頻率分布直方圖如圖8所示。

圖7 偏航誤差對比

圖8 偏航誤差頻率分布對比

由圖8可以看出，兩種控制策略下的偏航誤差角度主要分布在[-8,8]，基本滿足偏航對風精度要求，而改進的新型偏航控制策略機組在小范圍偏航誤差內的概率分布更加集中，說明其對風精度高于傳統偏航控制策略下的對風精度。

為進一步分析，下文對均方誤差、平均絕對誤差、偏航時間及偏航次數進行比較。

均方誤差：

平均絕對誤差：

傳統策略偏航時間：新型策略偏航時間：

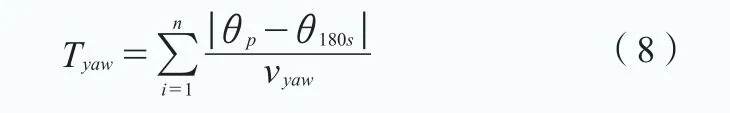
式中，N為風向采樣數，θp為當前機艙位置，θ180s為執行偏航前180秒平均風向，θpre為執行偏航前預測的風向，θpi為第i時刻的機艙位置，θwi為第i時刻的風向值，vyaw為偏航速度（取值0.5/s）。

由圖9和圖10可以看出，改進的新型偏航控制的機組與傳統機組相比，偏航次數由31次降到21次，偏航次數減少了32%；偏航時間由原來的515秒減少到193秒，偏航時間降低了62%。通過對偏航誤差統計，對風精度也有所提高，平均對風誤差由原來的8.11降低到7.86，均方誤差由10.4降低到10.04。對比結果見表1。

仿真結果表明，傳統偏航控制策略基本滿足對風要求，但偏航重啟次數較為頻繁，而改進的新型偏航控制系統可以在更少的偏航次數下滿足對風要求，且精度高于傳統偏航控制，說明新型偏航控制策略具有更好的控制效果。偏航次數和偏航時間的減少可有效降低偏航過程中的機械磨損，提高機組的可靠性和安全性。

圖9 偏航時間對比

圖10 偏航次數對比

結論

在大量的風電機組偏航控制策略研究中，偏航滯后的問題一直沒有得到有效解決。在風向變化頻繁的情況下，應結合風向變化趨勢制定偏航控制策略，從而在提高對風精度的同時降低偏航重啟次數。本文提出的基于風向預測的新型偏航控制策略在風電機組偏航重啟前根據歷史風向數據建立相應的ARIMA預測模型，并根據預測的平均風向進行偏航控制，結合風向變化趨勢的偏航控制提高了偏航系統的對風性能。通過仿真驗證，ARIMA模型預測的短期平均風向預測精度較高，應用基于ARIMA預測模型偏航控制策略的機組能夠更好地滿足對風要求，提高對風精度，減少偏航啟停次數。

表1 偏航控制策略對比

攝影：馬強