應用狀態方程預測液化天然氣的熱物理性質

苑偉民

中石化北海液化天然氣有限責任公司，廣西北海 536000

液化天然氣通常儲存在壓力為5～25 kPa、溫度為-163℃左右的低溫儲罐內。液化天然氣管路系統主要用于天然氣液化裝置與液化天然氣裝卸碼頭裝置，液化天然氣裝卸碼頭裝置與接收終端的液化天然氣儲罐，以及液化天然氣儲罐與氣化器的連接[1]，管路內的平均壓力在1 MPa左右，平均溫度在-156℃左右[2]。本文選取SRK、PR、LKP和MBWRS[3]四個狀態方程，對罐內儲存和管路輸送狀況下的液化天然氣的熱物理性質進行預測，并對預測的結果進行分析、討論。

目前，用于液態烴類計算的狀態方程主要有SRK、PR、LKP和MBWRS四個狀態方程，其中用于計算液化天然氣物性的主要是LKP狀態方程[2，4，5]，SRK和PR方程[6]多用于計算烴類的汽液平衡[7-15]，由于MBWRS狀態方程[16]形式復雜，文獻中較少用于液態計算[1]。本文運用四個狀態方程對液化天然氣的熱力學性質進行預測，重點對MBWRS狀態方程在預測液化天然氣熱物理學性質方面的適用性進行分析。

1 狀態方程

1.1 Soave-Redlich-Kwong（SRK）狀態方程[16]

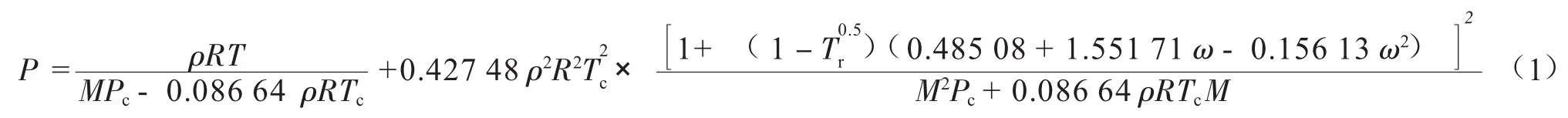
式中：P為系統壓力，kPa；ρ為流體密度，kg/m3；R為通用氣體常數，kJ/（kmol·K），取8.314 3；T為系統溫度，K；M為流體平均摩爾質量，kg/kmol；ω為Pitzer偏心因子；Pc為臨界壓力，kPa；Tc為臨界溫度，K；Tr為對比溫度，無量綱。

1.2 Peng-Robinson（PR）狀態方程[16]

兩參數立方方程，如SRK和PR狀態方程，其最佳適用范圍為：對于大多數烴類，偏心因子ω為0.35左右，亦即臨界壓縮因子Zc為0.26左右；對于氟化氫，ω為0.12左右，對于水，ω為0.229左右，對于惰性氣體，ω為0.286～0.311[10-11]。

1.3 Lee-Kesler-Plocker（LKP）狀態方程[4]

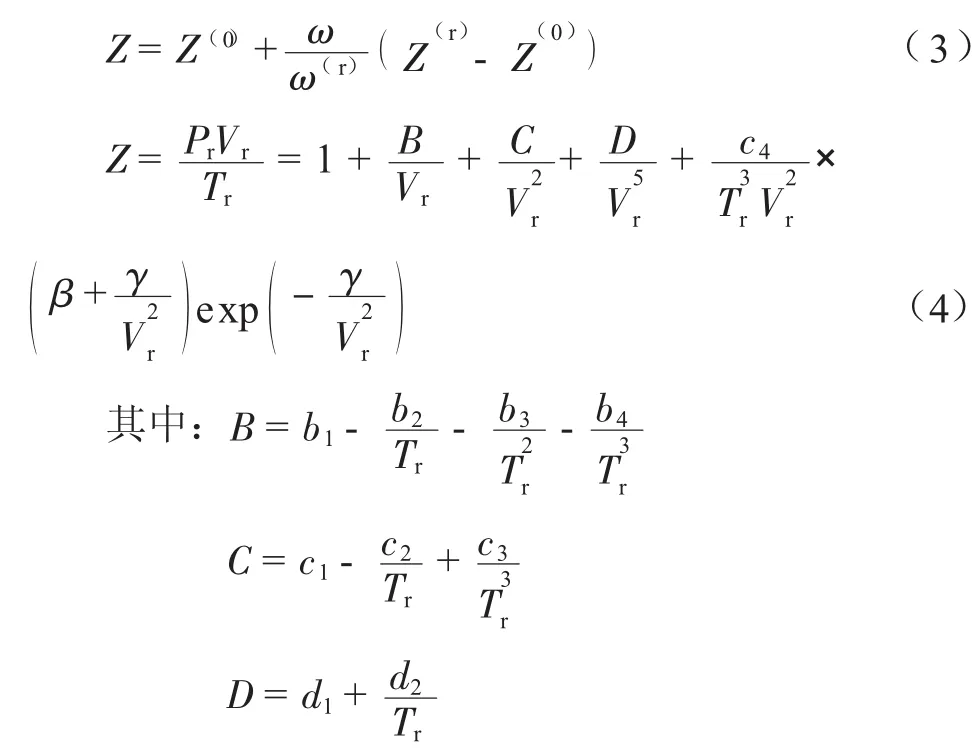
混合物的虛擬臨界屬性表達式為：

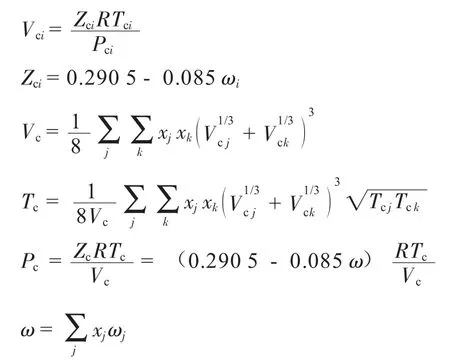
式中：Pr、Tr、Vr分別表示對比壓力、對比溫度、對比摩爾體積，無量綱；上標（0）、（r） 分別表示簡單流體和參考流體；下標i、j、k代表流體的組成；下標c表示臨界狀態；Vci表示第i種流體的臨界體積，kmol/m3；Zci表示第i種流體的臨界壓縮因子，量綱為1；xj、xk分別代表組分j、k的摩爾分數；Tci表示第i種流體的臨界溫度，K；Pci表示第i種流體的臨界壓力，kPa；ωi表示第i種流體的Pitzer偏心因子；b1、b2、b3、b4、c1、c2、c3、c4、d1、d2、β、γ為常數，其取值見表1。

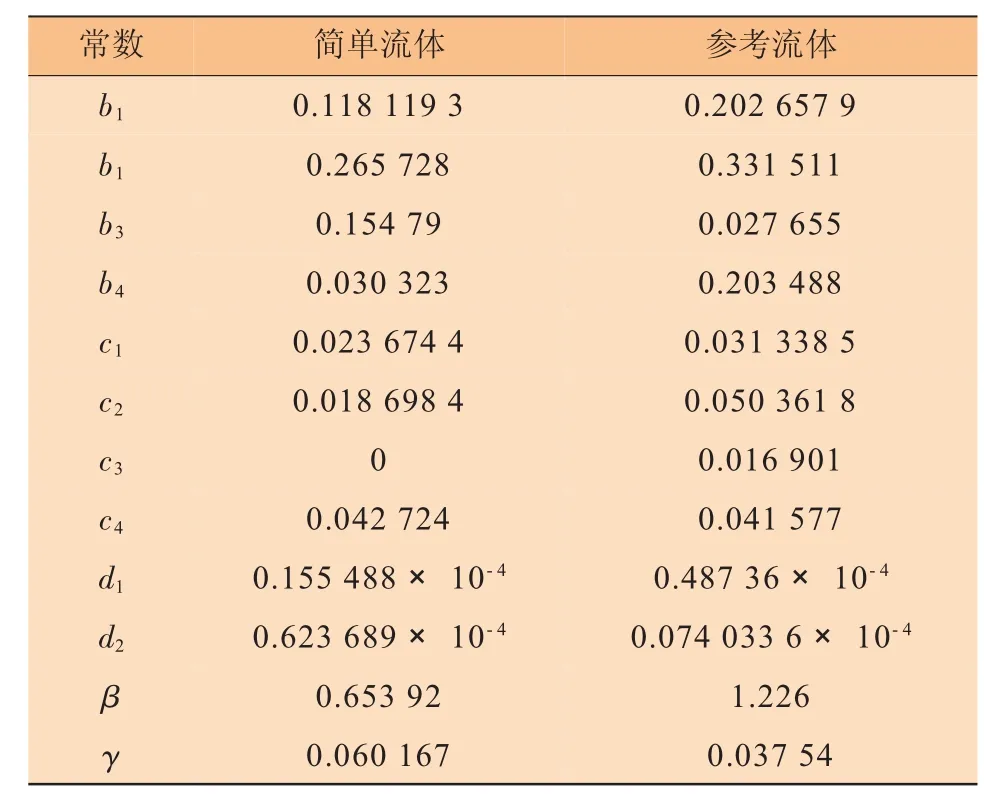
表1 常數的取值

1.4 Modified-Benedict-Webb-Rubin-Starling（MBWRS）狀態方程[3]

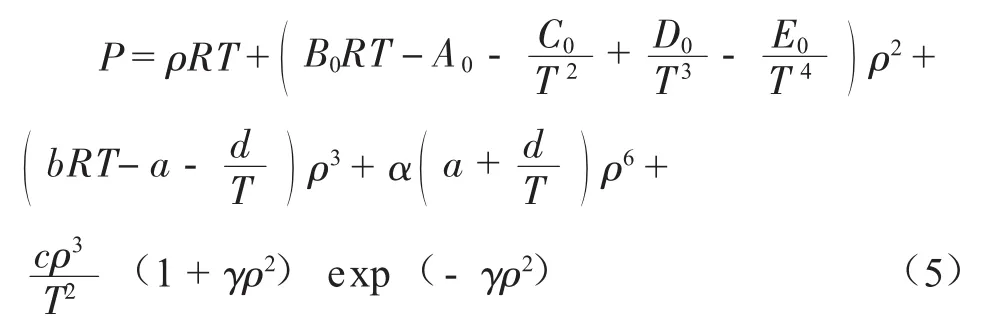
式中：P為系統壓力，kPa；T為系統溫度，K；ρ為氣相或液相的密度，kmol/m3；R為通用氣體常數，kJ/（kmol·K），取 8.314 3；A0，B0，C0，D0，E0，a，b，c，d，α，γ為方程中的11個參數[3]。

2 狀態方程分析

PR和SRK狀態方程廣泛應用于工業，特別是煉化和油氣儲層模擬。這兩個狀態方程的優點在于需要較少的輸入參數（僅需要臨界屬性和偏心因子這些普通數據），計算時間短，并且能夠較好地預測烴類的相平衡，這些對工藝流程設計很重要。然而，這兩個方程也有其短處，例如，不能很好地預測液相密度，大約有5%～10%的誤差，尤其是在接近臨界點時誤差更大，對于小于1.333 2 kPa的蒸汽壓預測也不十分準確。雖然有這些缺點，SRK和PR方程仍是在工業中廣泛應用的立方方程[17-19]。

BWR類型的狀態方程屬于擴展的維里方程的一種，可以把BWR類型的方程看成是一個封閉的維里方程，其包含的指數項可以看成是關于摩爾密度的無限級數項。最常用的是1972年STARLING K E和HAN M S提出的BWRS狀態方程，最近該方程又被擴展應用至25種氣體組分[3]。

STARLING KE和HAN M S使用BWRS狀態方程成功預測了38種混合物的超過1 400個數據點，包括LPG和天然氣（最多包含10種物質）。在溫度為-175～238℃和壓力為1.013×102～3.447×104kPa條件下預測得到的密度值，與實驗數據平均絕對偏差為1.16%；在溫度為-157～360℃和壓力為3.447×102～1.723×104kPa條件下預測的焓值，與實驗的焓值偏差為5.117kJ/kg；在溫度為-157～149℃和壓力為1.723×103～1.378×104kPa條件下預測的熵值，與實驗的熵值偏差為1.21×10-2kJ/（kg·K）。預測了包括正鏈烷烴、異丁烷、異戊烷、乙烯、丙烯、環己烷、苯、甲苯、氮、硫化氫、二氧化碳、硝酸氧化物在內的2 000個數據點，與實驗密度的平均絕對偏差為1.38%，與實驗焓值的偏差為4.047kJ/kg，與實驗的飽和蒸汽逸度偏差為1.08%[20]。

LKP狀態方程可以看成是使用對比態方法表示的BWR型狀態方程。

3 計算實例

選取北海液化天然氣接收站的工藝參數，對液化天然氣的熱物理性質進行求解。

3.1 管輸液化天然氣

取管道輸送部分絕對壓力為1 000 kPa，溫度為-158℃，求得對比壓力Pr為0.217 6，對比溫度Tr為0.595 7。使用HYSYS2006中SRK、PR、LKP方程求解，對MBWRS自行編程求解，組分見表1，結果見表2。

表1 L NG典型氣質組分（體積分數）

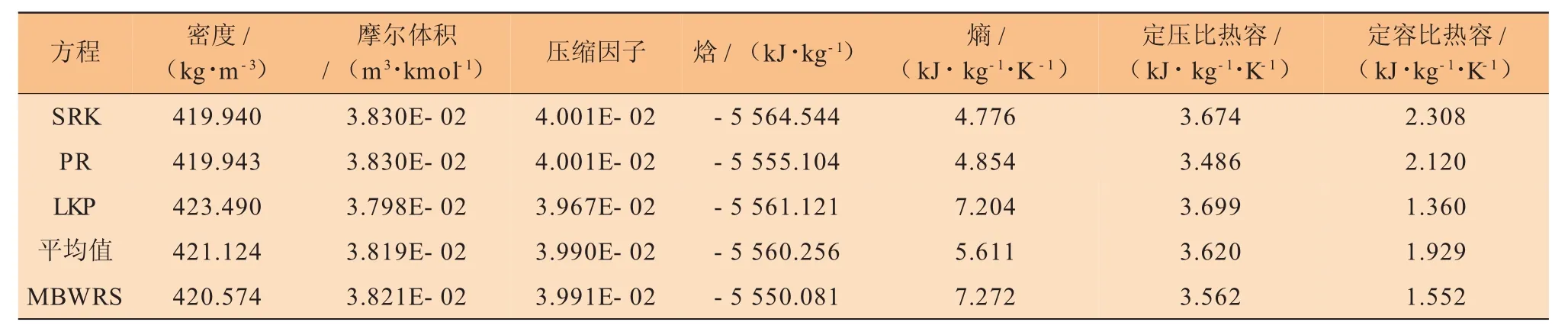
表2 L NG熱物理性質預測結果

3.2 LNG儲罐內液化天然氣

卸船期間，全包容罐儲罐最大允許操作壓力為25 kPa。取正常操作非卸船工況壓力為20 kPa，即絕對壓力為121 kPa，溫度為-162℃，求得對比壓力Pr為0.026 3，對比溫度 Tr為 0.575。使用 HYSYS 2006中SRK、PR、LKP方程求解，對MBWRS自行編程求解，結果見表3。

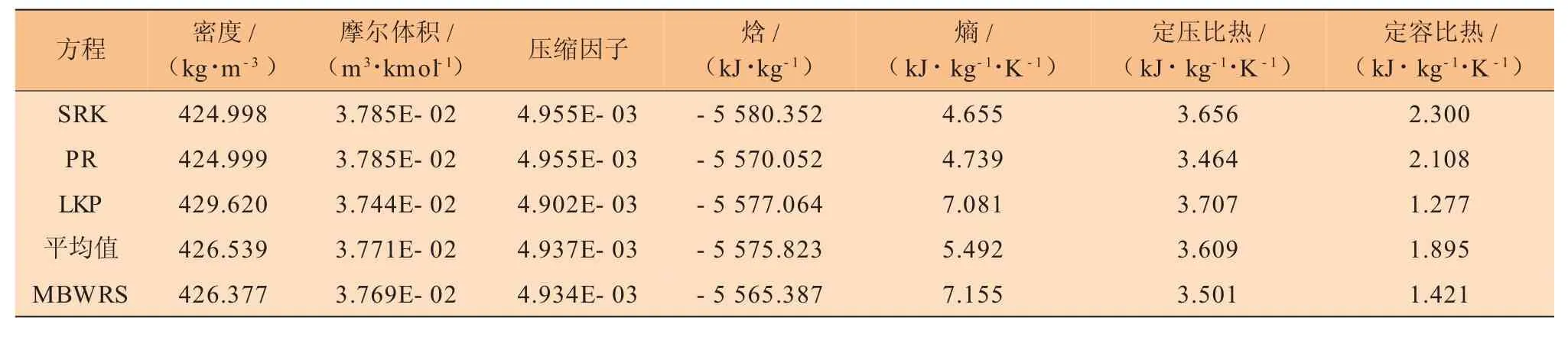
表3 L NG熱物理性質預測結果

4 結論

使用SRK、PR、LKP和MBWRS狀態方程對液化天然氣的熱物性參數進行了計算：

（1）從兩個實例計算的結果可以看出，第一種工況，SRK、PR和LKP狀態方程對密度的預測結果基本一致，MBWRS與SRK、PR狀態方程對密度的預測結果相近，LKP方程對密度的預測值與其他三個方程相差較大；第二種工況，MBWRS狀態方程對密度的預測值介于四個狀態方程之間，MBWRS和LKP狀態方程對密度的預測值偏大。

（2）兩種工況下，MBWRS方程預測的密度、摩爾體積、壓縮因子與SRK、PR、LKP三個方程預測結果的平均值基本一致。

（3）由于預測理想氣體焓、熵和比熱的經驗公式較多，以上方程預測的值相互之間也有較大出入。

（4）雖然兩種工況（Tr=0.595 7，Pr=0.217 6與Tr=0.575，Pr=0.026 3） 均超出了MBWRS狀態方程的適用范圍（Tr≥0.3），但是，從預測結果可以看出，使用MBWRS計算，預測值在一定誤差范圍內仍然準確。

（5）液化天然氣的運輸和存儲過程的壓力和溫度條件在MBWRS狀態方程的適用范圍內，計算結果可靠。

綜上所述，將MBWRS狀態方程用于液化天然氣工藝計算是準確、可行的。

[1]顧安忠，魯雪生，汪榮順，等.液化天然氣技術[M].北京：機械工業出版社，2004.

[2]陳保東，李慶杰，洪麗娜，等.液化天然氣管道輸送工藝參數的計算[J].油氣儲運，2011，30（1）：15-17.

[3]苑偉民.修改的BWRS狀態方程[J].石油工程建設，2012，38（6）：9-12.

[4]石玉美，顧安忠，汪榮順，等.天然氣物性的LKP方程求解[J].能源技術，2001，22（2）：62-64.

[5]位雅莉.天然氣液化工藝模擬與分析[D].成都：西南石油學院，2004.

[6]苑偉民，賀三，袁宗明，等.求解BWRS方程中密度根的數值方法[J].天然氣與石油，2009，27（1）：4-6.

[7]梁平，王治紅，李志銘，等.基于SRK狀態方程的烴類液相密度計算校正[J].西南石油大學學報（自然科學版），2009，31（3）：118-120.

[8]陳雪，李明.LNG儲罐內BOG動態模擬研究[J].油氣儲運，2008，27（11）：36-40.

[9]熊光德，毛云龍.LNG的儲存和運輸[J].天然氣與石油，2009，27（1）：4-6.

[10]童景山，高光華，高裕品.化工熱力學[M].北京：清華大學出版社，1995..

[11]王紅，白改玲，李艷輝，等.LNG接收站流程模擬計算[J].天然氣工業，2007，27（11）：108-109.

[12]金光，李亞軍.LNG接收站蒸發氣體處理工藝[J].低溫工程，2011，179（1）：51-56.

[13]李朋，鄧靜.LNG輕烴分離流程的優化研究[J].新疆石油天然氣，2010，6（1）：78-81.

[14]李軍，吳洪松.液化天然氣相平衡計算[J].煤氣與熱力，2007，27（10）：18-21.

[15]苑偉民，青青，袁宗明，等.輸氣管道模擬狀態方程[J].油氣儲運，2010，29（3）：194-196.

[16]童景山.流體熱物性學——基本理論與計算[M].北京：中國石化出版社，2008.

[17]HASAN O，STANLEY I，SANDER.Modeling vapor-liquid equilibria：Cubic equations of state and their mixing rules[M].United Kingdom：Cambridge University Press，1998.

[18]STANLEYI，SANDER.Models for thermodynamic and phase equilibria calculations[M].New York：MarcelDekker，lnc.，1993.

[19]苑偉民.PR氣體狀態方程的顯式化[J].油氣儲運，2017，36（5）：532-536.

[20]STARLING K E，HANM S.Thermo data refined for LPG（14）Mixture[J].Hydrocarbon Processing，1972，51（5）：129-132.