碳排放限額約束下的企業(yè)動態(tài)生產決策研究

蘭梓睿，孫振清，靖富營

（1.天津科技大學 經濟與管理學院，天津 300222；2.電子科技大學 經濟與管理學院，成都 610054）

0 引言

碳排放問題已經成為全球學者研究的最熱門方向之一，針對碳排放減少問題，各個國家或地區(qū)已經紛紛提出了自己的減排目標和減排政策，其中作為碳排放規(guī)制政策之一的碳排放限額政策也得到了大多數(shù)國家的普遍應用。碳排放限額政策的實施給高碳企業(yè)在經營管理中帶來了挑戰(zhàn)，同時也成為其在生產經營中不得不考慮的決策因素。目前，在碳排放限額政策下高碳企業(yè)生產決策研究中，主要研究體現(xiàn)在碳排放限額背景下的企業(yè)制造/再制造生產決策等方面的研究[1-3]，供應鏈管理研究[4-6]和訂貨決策研究[7]等，但是少有學者的研究興趣在于碳排放高的企業(yè)收集數(shù)據信息等預測時域問題，尤其在碳排放限額政策背景下。

收集并解析未來多長時間的有效數(shù)據是碳排放高的企業(yè)在生產決策時面臨的第一問題。這一類問題被定義為預測時域問題。碳排放限額背景政策下，預測時域的多少與高碳排放的企業(yè)生產批量的生產決策緊密聯(lián)系，這是因為預測時域的大小影響著未來數(shù)據信息（需求、成本等）收集與解析，預測時域偏長代表了未來一段時間將有更多的數(shù)據信息需要收集和解析，進一步預示了需要投入更多的人、財、物和時間成本從而提高了預測費用，然而當時間越來越長，所收集到的數(shù)據信息的準確性也逐漸變低，所以每個決策階段的后半部分所獲取的數(shù)據信息對前半段時間內生產決策的影響也慢慢變得不可信；而預測時域的偏短可能會導致獲取到缺失的信息數(shù)據，但是當前的決策結果得不到保證[8]。因而，在碳排放限額政策約束下，預測時域的大小和合理性將直接關系著高碳排放企業(yè)的費用大小和生產決策結果的可利用性，從而影響了該企業(yè)在運營管理中的效率。

本文考慮了碳排放限額政策構建了成本最小化模型，并且在此基礎上提出相對應的網絡流問題，分析得到包括最小成本解等在內的特性，不僅進一步建立了再生集合，而且設計出此研究方向的動態(tài)規(guī)劃方法從而尋找到預測時閾以及各個影響因素。借助數(shù)值實驗方法分析得出當高碳排放企業(yè)的生產固定成本和缺貨成本增加了，預測時閾隨之增加；而當該企業(yè)的倉儲成本增加了，預測時域將降低，從而為高碳企業(yè)（鋼鐵、電力、化工企業(yè)等在生產過程中產生高碳排放的生產企業(yè)）進行生產決策提供了合理的建議，也為政府給予高碳企業(yè)進行低碳生產、轉型補貼提供了理論依據。

1 模型構建

碳排放限額約束具體指高碳企業(yè)進行生產所需要的碳排放配額是政府限定的，當碳排放配額過剩或缺少時，企業(yè)不能在碳排放權交易市場出售或購買排放權。本文只考慮碳排放配額缺少的情況，因為碳配額過剩等同于配額不受限，并不影響高碳企業(yè)的生產決策。碳排放限額約束下，高碳企業(yè)由于碳排放配額受限造成了該企業(yè)缺貨，而且缺貨策略是過期不補，只在當期產生缺貨成本。

在正式構建模型前，需要對以下符號進行定義和說明：

T：時間周期；

P(t)：t-周期問題，t=1，2，···，T；

xt：在t周期期初產品的生產數(shù)量，t=1，2，···，T；

dt：周期t產品的需求，t=1，2，···，T；

It：在t周期期末產品的庫存數(shù)量，t=1，2，···，T；

St：碳排放限額約束下的周期t產品缺貨數(shù)量，t=1，2，···，T;

pt：單位產品的生產成本；

ht：單位周期內單位產品的倉儲持有成本；

σt：固定成本；

st：碳排放限額造成的單位缺貨成本；

令：

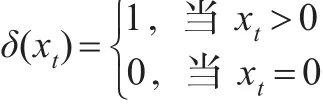
在本文中暗含如下假設：

假設1：缺貨過期不補，且缺貨成本大于單位生產成本，即st＞pt。

以上假設界定了所研究問題的環(huán)境，假設也是符合現(xiàn)實的，假設1，如果當期缺貨成本小于生產成本，則各期需求都不會被滿足，因為企業(yè)不生產是最優(yōu)的。假設2描述了此問題中成本變動是有條件的，并且涉及到了一種特殊情形（單位產品不變的缺貨成本），也適用于小幅度范圍內波動的單位缺貨成本情形，在現(xiàn)實中，企業(yè)為降低庫存持有成本，都盡可能滿足當期的需求，而不是當期需求缺貨而持有庫存滿足未來周期需求。

碳排放限額政策背景下的高碳排放企業(yè)包括多周期在內的生產計劃問題將借助以下優(yōu)化決策模型刻畫。高碳排放企業(yè)的生產計劃目標是在T周期內達到固定成本，生產成本，倉儲持有成本和缺貨成本之和最小，目標函數(shù)表示為：

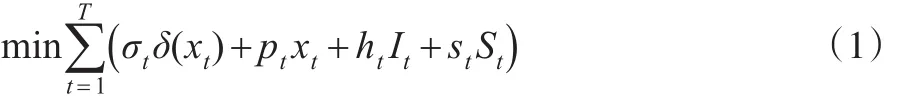
約束條件：

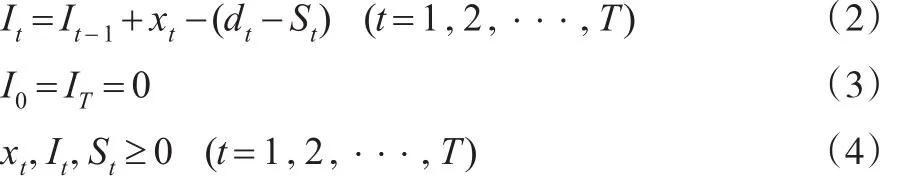
約束條件（2）表示商品產出數(shù)量、缺貨數(shù)量和需求之間的關系。為了滿足一般性情況，本文將初始時期和結束時期的庫存假設為0，也就是約束條件（3）。約束條件（4）表示生產數(shù)量，庫存數(shù)量以及缺貨數(shù)量的非負性。

依據上述問題的刻畫，也可以利用圖1所示的網絡流問題再一次描述所研究問題。節(jié)點1，2，…，T代表各周期的需求，如t期的需求為dt，節(jié)點P代表利用生產使得各周期的需求得到供應，節(jié)點S代表通過缺貨滿足各周期的需求，有向弧(t，t+1)代表通過上一周期所剩余的庫存滿足下一個周期需求。參考費用與網絡流，可以發(fā)現(xiàn)如下性質：

（1）有向弧(P，t)代表生產xt的費用流，假設xt=0，此費用流為0；假設xt＞0費用流為σt+ptxt。

（2）有向弧(t，t+1)代表庫存費用流，假設It=0，此費用流為0；假設It＞0費用流為htIt。

（3）有向弧(S，t)代表缺貨St的費用流，假設St=0，此費用流為0；假設St＞0費用流為stSt。

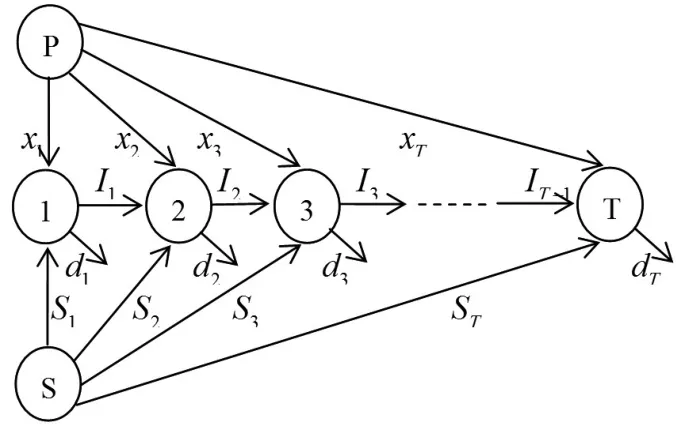
圖1 缺貨情況網絡流問題

2 碳排放限額約束下的預測時閾分析

2.1 最優(yōu)解性質

定理1：在T周期最優(yōu)解，則每個連續(xù)的周期形成一個再生集。

假設在一個最優(yōu)解中存在個連續(xù)的周期沒有形成一個再生集，即周期t，t+1，..，t'庫存都為正，又由上文可得，t期期初生產數(shù)量至多覆蓋到周期t'-1，因此可得周期t，t+1，..，t'至少有一期庫存為零，符合再生集的定義，因此每個連續(xù)的周期形成一個再生集。

定義2：在t周期生產的最小數(shù)量為的最小整數(shù)，t=1，2，..，T。

定理2：在T周期最優(yōu)解中，有：

證明：

（1）類似Wagner和Whitin(1958)[9]，略。

（2）運用反證法，假設It·St＞0 ，由圖1可得，此時的一單位產品的路徑為從節(jié)點M到節(jié)點t+1，需要經過節(jié)點S和節(jié)點t，費用流為st+ht。如果變換一條路徑，僅經過節(jié)點S，由有向弧(S，t+1)產生的費用流為st+1，比原路徑費用要低，與假設矛盾，因此，在T周期最優(yōu)解中，有It·St=0，t=1，2，..，T。

（3）運用反證法，假設xt·St＞0 ，若 0＜xt＜dt，因為pt＜st，所以增加一單位xt可以降低成本(st-pt)，若xt=dt且It＞0 ，則有It·St＞0 ，與定理 2矛盾，因此若xt=dt，有It=St=0 ，與原假設xt·St＞0 矛盾；若xt＞dt，此時It＞0 ，則有It·St＞0 ，與定理2矛盾，因此St=0，與原假設xt·St＞0矛盾。綜上可得，在T周期最優(yōu)解中，有It·St=0 ，t=1，2，..，T。

（4）在T周期的最優(yōu)解中，假設即，變形為st·xt＜σt+pt·xt，此不等式意味著t周期生產xt數(shù)量的產品的成本大于缺xt數(shù)量的產品的成本，與假設矛盾，故

2.2 預測時閾分析

定理3：考慮P(t-n+1),P(t-n+2),…,P(t)問題如 果對 于j=1，2，…，τ（1≤τ≤t-n+1）成立，則t為預測時閾，τ為決策時閾。

證明：根據Ludin和Morton決策時閾和預測時閾理論[10]，如果再生集中的每一個子問題都有相同的周期決策，這個決策也是更長周期問題的最優(yōu)決策。由定理1，每n個連續(xù)的周期形成一個再生集。當解P(t-n+1),P(tn+2),…,P(t)問題時，從t-n+1期到t期有n個周期，在更長時期的最優(yōu)解中，這n期中至少有一期期末庫存為0，因此這些生產序列至少有一個是更長周期t*(t≤t*)的最優(yōu)解的一部分。如果對于i=1，2，…，τ成立，意味著每一個問題P(t-n+1),P(t-n+2),…,P(t)有相同的τ期最優(yōu)生產子序列，因此這個τ期子序列被包含于任何更長周期t*(t≤t*)最優(yōu)解的一部分，則τ為決策時閾，決策時閾需要t周期的信息，所以t為預測時閾。

2.3 前向算法

由于上述定理可發(fā)現(xiàn)，碳排放限額約束下高碳企業(yè)的動態(tài)批量預測時閾問題可以通過前向遞歸動態(tài)規(guī)劃算法解決。

由定理2可得t-周期問題可以分解為一系列的子問題解決，令P(q，t)代表周期q到周期t，且滿足Iq-1=It=0;Ij＞0,i=q，…，t-1;xq＞0 的子問題。C(q，t)表示P(q，t)的最優(yōu)成本。

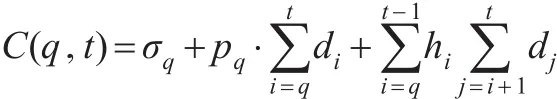
令F(t)代表P(t)問題的最優(yōu)成本，則：

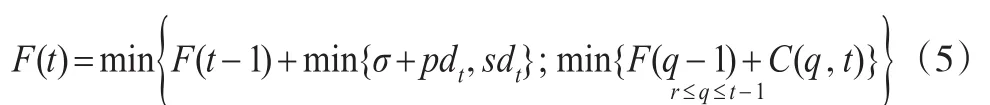
3 數(shù)值實驗及討論

本文通過構造數(shù)值試驗來進一步理解碳排放限額約束下的企業(yè)動態(tài)生產決策預測時閾特征。通過函數(shù)Dt+1=D0(1.0)t來產生各周期的需求均值，當需求均值確定之后，各周期的實際需求通過函數(shù)Dt+1=D0(1.0)t+0.5D0ξ產生。其中ξ為標準正態(tài)變量，任何情況下，如果產品需求小于1則設定為1。基準需求設為D0=10。為了簡化實驗而且能滿足本文的假設條件，圖2參數(shù)設為st=6；pt=2 ；ht=1；σt取 60，70，80，90，100，150，200這 7個值。圖3參數(shù)設為σt=60；pt=2；st=6；ht取0.5，1，1.5，2，3，5，70這7個值。圖4參數(shù)設為σt=60；pt=2；ht=1；st取5，6，7，8，9，10，11這7個值。為了方便找到預測時閾中值，對每一組參數(shù)運行15次，每一組實驗運行的次數(shù)為7×15=105。

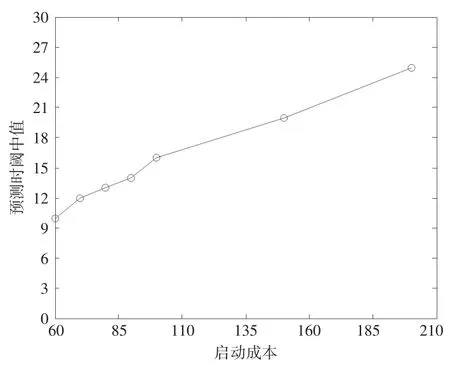
圖2 作為啟動成本函數(shù)的預測時閾中值

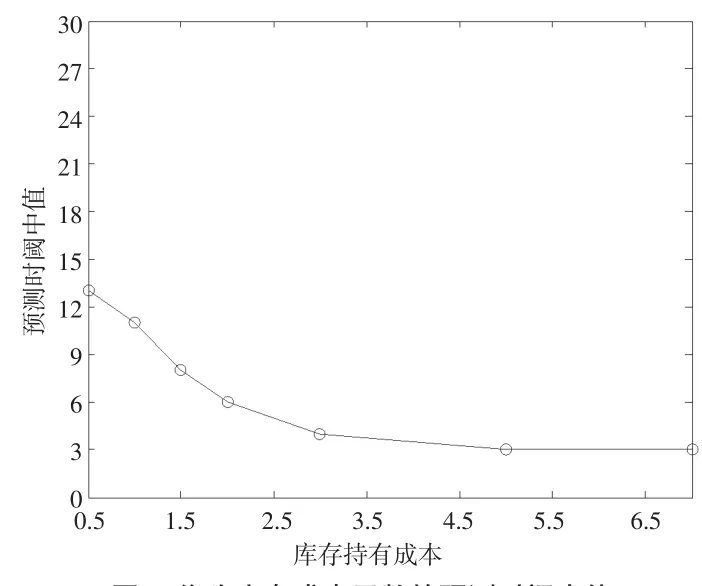
圖3 作為庫存成本函數(shù)的預測時閾中值

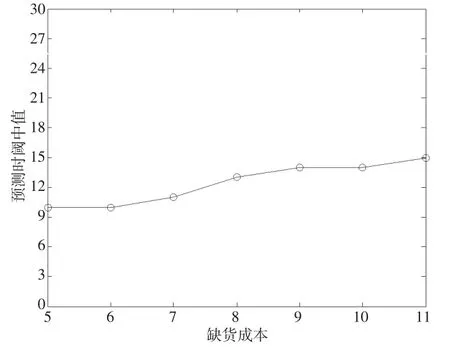
圖4 作為缺貨成本函數(shù)的預測時閾中值

在碳排放限額背景下，由于每一期的碳排放配額存在不夠用的情況，而且沒有碳排放權交易市場進行碳排放配額的買賣，所以碳排放限額的約束改變了原來的及時交貨方式而變?yōu)槿必浄绞健８鶕?shù)值實驗得出來的圖2至圖4，可以得到單一變量下預測時閾與企業(yè)生產過程的固定成本、倉儲成本和缺貨成本之間的相互關系。當高碳排放企業(yè)的固定啟動成本和缺貨成本增加了，預測時閾隨之增加；而當該企業(yè)的倉儲持有成本增加了，預測時域將降低。因為啟動成本相比于庫存持有成本較小時，啟動的次數(shù)較多，每一次啟動所覆蓋的周期數(shù)較小，產生的再生點較多將會導致再生集比較小，因而預測時閾較小。而啟動成本相比于庫存持有成本很大時，每一次啟動所覆蓋的周期數(shù)較多，導致再生集較大，因而預測時閾較長。這也可以告訴企業(yè)，如果啟動成本相比較庫存持有成本小，則當高碳排放企業(yè)在做包括生產決策在內的運營管理中只需要將未來較短時間內的市場數(shù)據作為參考標準，反之則為了確定更為精確的動態(tài)批量需要考慮未來偏長時間的數(shù)據信息。由于碳排放配額有限導致的缺貨情況下，缺貨策略決策柔性較大，增加了每個周期決策的復雜性。如果產品的缺貨成本較大導致再生集長度的增加，進一步增加了預測時閾的長度。因為從上述分析可以看出，碳排放限額政策增加了高碳企業(yè)的預測時閾，從而增加了企業(yè)的預測成本，高碳排放企業(yè)在碳排放限額政策背景下，為了獲取更為精確的生產批量需要將偏長時間的周期的數(shù)據信息作為參考標準。

綜上分析，碳排放限額政策約束下高碳排放企業(yè)在安排生產計劃在內的運管管理中，需要考慮到未來費用等因素的影響，而缺貨成本、固定成本、倉儲持有成本和需求特性等多種因素的變動又將對獲取和解析未來一段時間的數(shù)據信息進行影響，所以高碳排放企業(yè)為了獲得精準而合理的決策結果必須將上述分析的各種因素納入考慮范圍內。

4 結論

本文借助數(shù)值仿真方法分析得到高碳排放企業(yè)的原有預測時閾將受到碳排放限額政策的沖擊，首先這些企業(yè)需要改變決策前的預測時閾安排生產計劃，再者國家相關政府部門實施碳排放政策也會從中借鑒，碳排放限額政策的實施進一步增加了生產計劃安排的不確定性，也會對企業(yè)的決策費用帶來一定沖擊，所以國家出臺的碳排放限額政策將增加高碳排放企業(yè)的預測時閾從而加大了其預測費用，也進一步加大了企業(yè)其他的生產管理費用，這一結論也為國家如何補貼低碳生產企業(yè)，補貼多少做了理論回答。預測時閾大導致高碳企業(yè)進行低碳生產、轉型時所產生的預測成本大，因而政府進行低碳生產的補貼要高；反之預測時閾小，高碳企業(yè)進行低碳生產、轉型所產生的預測成本也小，政府對這些企業(yè)的補貼也可相應減少。