基于平方根迭代UPF濾波的無源定位算法研究

汪語哲，楊正凱，王 寧，李云昭，初昕宇，冉春秋

(大連民族大學 a.機電工程學院；b.大學生創新創業教育中心，遼寧 大連 116605)

僅有角度測量的固定輻射源無源定位問題是一個經典的導航問題。在現代戰爭中，快速定位對飛行器有威脅的基地輻射源如雷達、電子干擾源和紅外輻射源等可以較大程度提高戰斗飛行器的生存能力。在航行過程中，空間飛行器為了防止敵方雷達跟蹤，常常需要關閉向外部發射電磁波來探測目標位置和速度的主動探測裝置(如機載主動雷達等)，而靠僅能夠測量視線角的被動接收裝置來接收目標能量輻射以保證自身安全。這種被動式定位方式作用距離遠，接收隱蔽，不易被對方察覺，對于增強系統在復雜電磁環境下的生存能力和工作能力具有重要意義，是飛行器定位輻射源的常用方法[1]。此外，海上遇難搜救電子偵察定位、空間飛行器測控、衛星定位等問題也同樣屬于無源定位問題。因此，無源定位問題的研究具有重要的意義和廣闊的應用前景。

現有的固定輻射源無源定位，研究的重點在于定位精度、收斂速度和算法效率。最早的定位估計方法是直線(兩點)定位算法，以及最小二乘估計算法(Least Square Estimate,LSE)[1]。LSE是一種數據批量處理方法，計算中收斂速度較慢，且僅當整個系統沒有噪聲干擾時，才能收斂到真值。隨后，擴展卡爾曼濾波算法(Extended Kalman Filter,EKF)作為一種非線性隨機函數逼近方法，得到了學者的普遍關注[2]。Spingarn注意到了LSE和EKF的相似性，采用EKF算法處理含噪測量方程，提高了定位的收斂速度和算法的效率。為了進一步提高定位的收斂速度，Challa等[3]提出一種測量線性化狀態方程的EKF定位方法。隨著計算機技術的高速發展，數據處理速度大幅度提高，很多計算量較大的算法已經可以用于處理無源定位等對于實時性需求較高的非線性估計問題。Gordon[4]考慮了采用粒子濾波作為無源定位算法，在某些條件下取得了比LSE和EKF算法更好的估計效果。

1 問題的描述

為使問題簡單化，并具有較強的代表性，考慮典型的平面無源定位模型如下：

(1)由于定位距離和地球半徑的數量級差距在100倍以上，可以不考慮地球的球面效應；

(2)不考慮飛行器自身定位的導航誤差；

(3)不考慮目標的高度，只考慮二維平面的定位情況；

(4)將載機視為一個質點，且以速度v=v0沿某一方向(不與載機的初始位置和輻射源之間的連線方向重合)做勻速直線運動(載機的加速度a≡0)。

在上述假設條件下，一種典型的平面無源定位問題原理圖如圖1。飛行器沿輻射源邊緣做勻速直線運動，令飛行器在初始時刻(t=0)的位置表示為ξ0=(x0,y0)T。

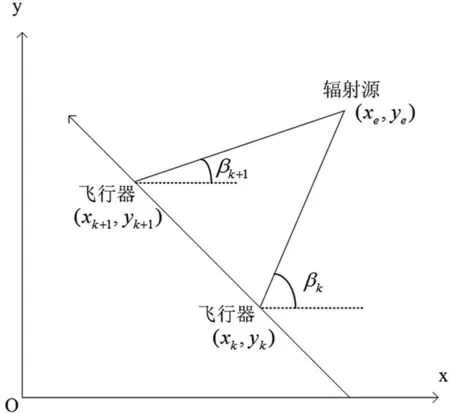
圖1 一種典型的平面無源定位問題原理圖

載機在k時刻的位置表示為ξk=(xk,yk)T，η=(xe,ye)T為輻射源的地理位置，則系統的數學模型可以描述為

βk=hk(xe,ye)+ωk；

(1)

(2)

設采樣周期為T，(vx,vy)表示載機的速度v0在x和y軸上的分量，載機在k時刻和初始時刻(t=0)的位置關系可以表示為

(3)

經離散化的系統觀測方程可以表示為

(4)

式中，ωk為系統的測量噪聲，簡單起見，假設ωk為高斯白噪聲，則有

(5)

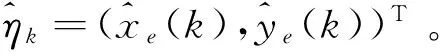
2 傳統濾波方法

無源定位問題的經典算法是粒子濾波算法(Particle Filter，PF)，該算法1993年由Gordon提出，一開始用于解決非線性估計問題，取得了較好的效果。然而隨后研究人員發現，該算法對于先驗概率密度函數的選取十分敏感，只有當先驗概率密度函數充分逼近被估計的非線性隨機系統的真實概率密度分布時，才能取得較好的估計效果。這是由于PF算法選取的提議函數不含任何觀測信息，在被估計系統的非線性非高斯程度較強時，收斂速度常常較慢，甚至難于收斂。針對這一問題，文獻[5]提出了采用EKF算法作為提議函數的改進粒子濾波算法，該算法稱為EPF。EPF在一定程度上提高了算法的收斂速度。然而，由于EKF算法本質上是一種對于非線性函數的一階泰勒逼近，在系統非線性程度較高時，EKF算法容易發散，EPF常常存在類似于EKF精度不高、收斂速度慢等問題。

3 濾波方法的改進

針對上述EPF算法存在的問題，文獻[4]提出采用UKF算法作為提議函數，取得了較高的估算精度。然而，UKF算法的三個參數影響著采樣點沿狀態均值的分布狀況。如果參數選擇不當，可能導致采樣半徑變大，影響算法的數值魯棒性和估計精度；在實際仿真過程中同樣發現，若三個參數選擇不當，則UKF算法運行常常出錯，這是由于當協方差矩陣P的行列式較小時，算法的數值魯棒性難以保障。針對這一問題，文獻[6]將標準UKF算法展開成矩陣平方根分解方式進行計算，設計了一種平方根迭代UKF (Square-root Unscented Kalman Fliter,SRUKF) 算法，在UKF迭代中采用了平方根作為迭代傳遞量，從而保證了協方差矩陣P的正定性。

3.1 SRUKF算法

(1)初始化：

(6)

式中，chol表示矩陣的克萊斯基分解，下同。

(2) Fork∈{1,2,…,∞},

a. Sigma點計算：

(7)

b. 時間更新：

χk|k-1=f[χk-1,uk-1]+E[vk-1] ；

(8)

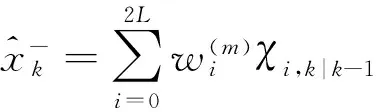
(9)

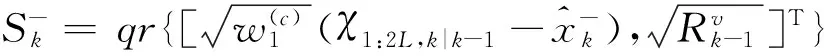
(10)

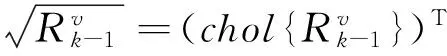
(11)

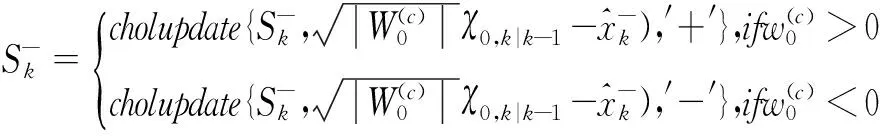
(12)

yk|k-1=h(χk|k-1)+E[nk] ；

(13)

(14)

c. 測量更新方程：

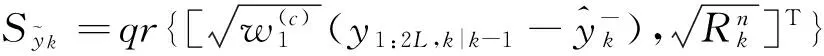
(15)

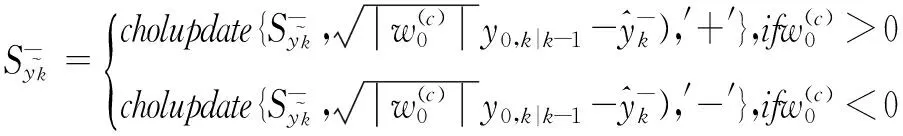
(16)

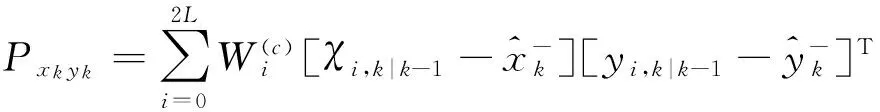
(17)

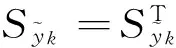
(18)

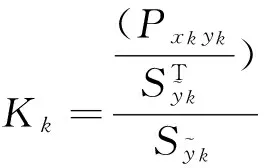
(19)

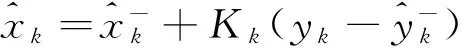
(20)

(21)

式中：U=[u1,u2,…,uNy]；Ny為測量向量維數。

對于i=1:Ny，

(22)

(23)

考慮到標準粒子濾波算法的缺陷，為了在保證不降低計算精度的情況下進一步提高計算效率，文章采用了SRUKF算法作為粒子濾波算法的提議函數，這里將其稱為SRUPF。

3.2 SRUPF算法

(1) 初始化：

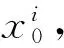
(24)

(2) 對于i=1,2,…,N，利用3.1給出的SRUKF算法更新粒子：

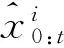
對于i=1,2,…,N,將重要性權值

(25)

作歸一化處理。

(3) SIR重采樣：

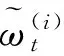
4 仿真結果

令固定輻射源位置為(xe,ye)=(226.92 km,226.92 km)，觀測者的初始位置(x0,y0)=(209.21 km,17.70 km)，并以定常速度vx=-0.161 km·s-1，vy=0.161 km·s-1沿直線飛行。從k=0時刻開始，每300 s對目標方位測量一次，測量噪聲的標準差σ=1°。

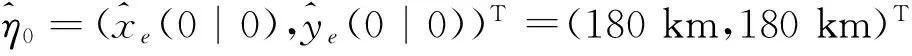
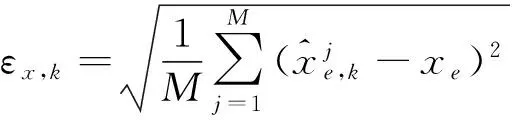
(26)

(27)

式中，M表示蒙特卡洛仿真的次數，作為一個低維參數估計問題，取較少的仿真次數就能夠很好地衡量估計的效果[7]，取M=20。文章所設計的UPF濾波器仿真結果如圖2。

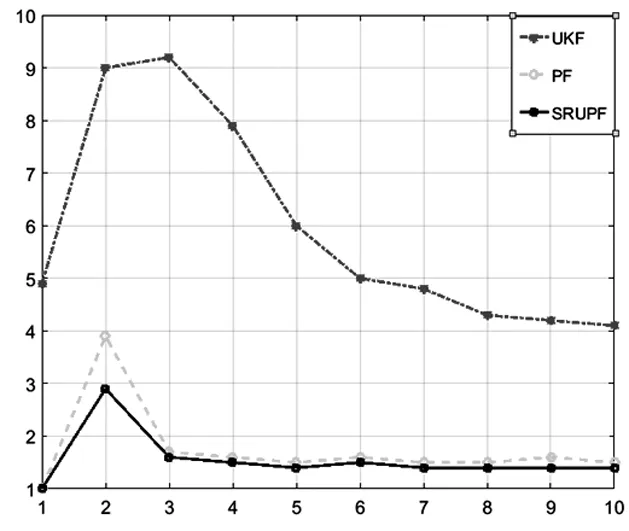
(a)X軸的RMSE估計誤差

(b)Y軸的RMSE估計誤差

從仿真結果的對比中發現，無論是X軸還是Y軸的位置，文章給出的SRUPF算法較PF和UKF算法相比，均具有更快的收斂速度和更高的估計精度。同時，計算得出，文章給出的SRUPF濾波器相比傳統UPF在計算效果基本相同的前提下，節省了17%的計算時間。

5 結 語

針對固定輻射源無源定位這一經典的參數估計問題，文章采用平方根迭代UKF算法作為提議函數，改進了傳統PF算法，給出了一種SRUPF算法的設計方案。仿真結果表明，文章所設計的SRUPF算法和標準粒子濾波器以及UKF濾波器相比，具有更高的估計精度，而且同標準UPF濾波器相比，在不降低計算精度的前提下，節省17%的計算時間。對于低維參數估計問題，UPF粒子濾波器具有更好的估計精度，計算量在硬件可承受范圍內，因此，是無源定位的一種較好的新型方法，對機動目標跟蹤問題的研究有一定理論意義和使用價值。

[1] KAEL S.Passive position location estimation using the extended Kalman filter[J].IEEE Transactions on Aerospace and Electronic Systems,1987(23):558-567.

[2] KLAUS B. An efficient method of passive emitter location[J].IEEE Transactions on Aerospace and Electronic Systems,1992(28):1091-1100.

[3] CHALLA S,FARUQI A. Nonlinear system-linear measurements approach to passive position location using extended Kalman filtering[C]. New York:IEEE TELCON-Digital Signal Processing Applications,1996: 665-669.

[4] 朱胤.非線性濾波及其在跟蹤制導中的應用[D].哈爾濱：哈爾濱工業大學，2009:59-71.

[5] 汪語哲.濾波技術在高超聲速大機動飛行器末制導中的應用[D].哈爾濱：哈爾濱工業大學，2013:19-51.

[6] FFATI K,SKONIECZNY M.EKF and UKF localization of a moving RF ground target using a flying vehicle [C].Windor:IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE),2017:1-4.

[7] OU X H; WU X; HE X X. Adaptive iterated UKF based node localization for WSN[J]. Chinese Journal of Sensors and Actuators,2015,28(2) :234-238.