基于簡易風洞的薄翼模型升力測量實驗
何建勛 唐 芳 熊 暢 王志超
(1北京航空航天大學能源與動力工程學院,北京 100191;2北京航空航天大學物理科學與核能工程學院,北京 100191;3北京航空航天大學數學與系統科學學院,北京 100191)
當前以飛機為主的航空飛行器扮演了越來越重要的角色,對航空飛行器工作原理的普及教育也愈加必要。簡單而言,大部分航空飛行能夠離開地面飛上天空,是因為通過對機翼翼型的氣動設計,翼型上下表面附近的空氣產生了壓力差。而該壓力差的綜合效果除產生升力外,還有沿來流反方向的分量,稱為翼型阻力,需要通過發動機提供推力與之平衡。在翼型設計中,需要盡量提高翼型升力、降低阻力。
翼型的升力可通過風洞實驗測得,大量的實驗結果表明,翼型的升力與來流速度、流體密度以及翼型形狀均有關。為研究翼型參數對升力的影響,消除流體的因素,可以引入升力系數的概念。升力系數是翼型的重要參數,通過實驗來研究不同形狀翼型的升力系數,及不同來流速度時升力系數與迎角的關系,對航空飛行器設計以及葉輪機械的設計等都有著重要意義。
對于無粘不可壓完全氣體翼型擾流和薄翼模型,可以通過對流場進行小擾動線性近似而獲得升力的解析解[1]。然而,由于其過程相對抽象,無專業知識的本科低年級學生很難理解。而如果能借助實驗對薄翼型升力理論進行驗證,會加深學生對模型和理論的理解[2],提升薄翼型理論的教學效果。
實驗選取展寬b=143mm、弦長l=224.5mm、最大厚度a=33.5mm的翼型,滿足薄翼型理論對翼型的要求。設計風速可調的簡易風洞,用空速管測量流速,利用不影響流體分布的彈簧測力裝置測量升力。改變迎角,研究不同流速下升力系數與迎角的關系。通過對實驗數據的分析可知,雖然簡易風洞存在不滿足理論模型的因素,但是并不影響參數變化的趨勢,得出的結論和薄翼型理論結果基本吻合,該實驗裝置也可用于其他自制模型的升力測試和研究。
1 薄翼型理論相關知識
由空氣動力學的相關知識,翼型的升力系數可以定義如下[3]
(1)
其中,Y為升力;CY為升力系數;ρ為流體的密度;v為來流速度;l和b分別為翼型的弦長和展寬。升力系數是在特定流動下翼型的參數,與流體的種類和流速無關。
由空氣動力學給出的薄翼型理論,對于不可壓無粘流體的翼型擾流,在翼型的厚度、彎度和迎角都不大時,繞流場可以認為是一個小擾動的勢流場,可以進行線性化近似[1]。在這種假設下,翼型升力系數由中弧線、厚度以及迎角唯一確定。對于確定的翼型,中弧線方程和厚度已經確定,迎角和升力系數存在一一對應關系。
于是薄翼型理論下的升力系數為[3]
其中,α為來流相對于翼型前緣的迎角;yf=y(x)為翼型中弧線方程;l為弦長。通過式(2)~式(5)就可以計算出升力系數與迎角的一一對應關系。
2 簡易風洞實驗裝置和測量過程
實驗用簡易風洞結構如圖1所示,鼓風機從外部吸入空氣,經收縮段加速后進入試驗段,提供不可壓縮的低速氣流,試驗段截面為矩形,寬度B=510mm,高度H=510mm。在試驗段放入翼型,空氣流經翼型表面使其產生升力,可在此進行實驗和測量,實驗后氣流通過擴壓段降速排出。

圖1 簡易風洞結構簡圖
一般的風洞實驗升力是利用風洞天平直接測量或通過打孔測翼型表面壓強分布而獲得。對于小型風洞,風洞天平的引入會嚴重改變翼型周圍的氣流分布。而打孔測翼型表面壓強分布在設備結構和數據處理上會比較復雜。本實驗所用的測力裝置和測迎角裝置分別如圖2(a)、圖2(b)所示。為了實現升力的測量,在風洞的頂部開一窄縫,實驗翼型的頂部安裝兩個鉸接細桿,翼型受升力作用時兩鉸接桿上移,推動彈簧使壓縮帶動指針示值發生變化,指針示值即可表示升力的大小。為保證升力示值的準確,用精度為0.1g的電子天平對彈簧升力計進行了校準。同時通過調節兩鉸接桿的上下位置可以固定和改變翼型的迎角,如圖2(b)所示迎角示值可以由彈簧秤座上讀數讀出為8°。

圖2(a) 測力裝置

圖2(b) 測迎角裝置
2.1 翼型中弧線方程的建立
本實驗所用翼型如圖3(a)所示,在剖面上建立平面直角坐標系,通過測量得到翼型上下表面對應位置點的坐標,取坐標平均值得到中弧線上一些點的坐標(x,y),由多項式擬合得到中弧線方程。中弧線的擬合結果如圖3(b),擬合方程為
(6)
其中,l為翼型的弦長;a為翼型中弧線的最大高度。

圖3(a) 實驗翼型圖片

圖3(b) 翼型中弧線擬合結果
取定一系列翼型迎角α,將式(6)代入式(3)、式(4),并結合式(2)和式(5)可以得到不同迎角對應的升力系數理論值CY0。
2.2 升力系數的實驗測量
借助簡易風洞,測量翼型升力、迎角和空氣流速。如前所述,翼型的升力由測力裝置直接讀出,迎角由彈簧秤座上的迎角刻度顯示。來流速度的測量借助于空速管[4],由不可壓流體的伯努利方程得來流速度的計算公式
(7)
其中,p*為流體總壓;p為流體靜壓;Δp為流體的總靜壓差;v為來流流速;ρ為流體密度。通過測量總靜壓差可以求得來流流速。
由式(2)~式(5)可以計算出不同迎角下的升力系數,實現簡易風洞對薄翼型理論的研究。
3 結果與討論
下面分別從實驗結果的重復性、線性度和空氣流速的影響3個方面討論,以論證簡易風洞研究薄翼型理論的可行性。
3.1 結果的線性度和重復性

圖4 升力系數測量值與迎角的關系。CY1、CY2、CY3為相同條件下重復測量的3組升力系數結果
多次重復測量不同迎角對應的升力系數如圖4所示。由圖4可知,升力系數與迎角的線性相關性較好,滿足薄翼型理論中“升力系數和迎角呈線性關系”的結論。而且相同實驗條件下多次重復測量不同迎角下的升力系數,如圖4所示3組數據的重復性也很好,且迎角越小重復性越佳。由此說明即使簡易風洞中的流動呈現強烈的非定常性,粘性的影響也不容忽略,實驗的重復性同樣可以得到滿足。
3.2 流速對結果的影響及與理論值的比較
由薄翼型理論可知,無粘定常流動下升力系數是翼型的參數,理論上與流體的種類及流速無關。通過調節風機的檔位改變來流速度,在不同來流速度下分別測量升力系數與迎角的關系。實驗結果做線性擬合如圖5所示。
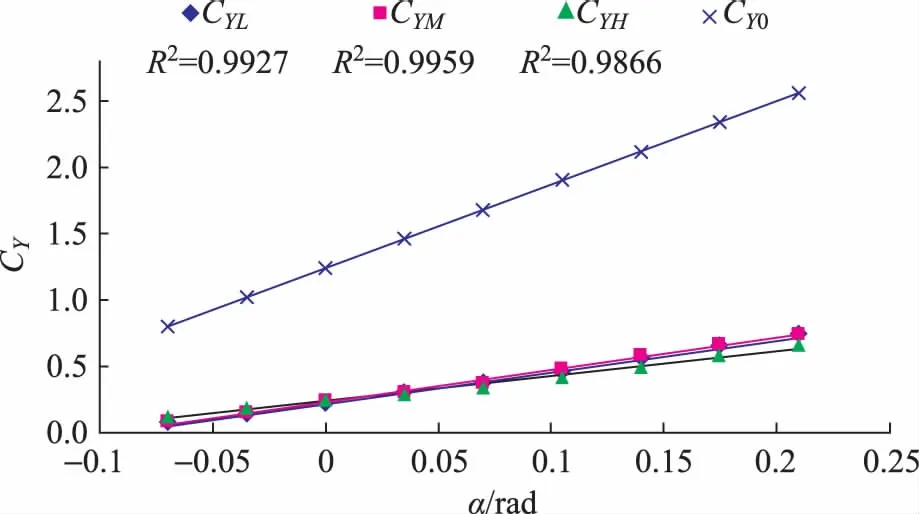
圖5 不同來流速度下升力系數的測量結果
圖5中CY0是升力系數理論結果,CYL、CYM、CYH分別為低、中、高流速下測量的翼型升力系數,來流速度大小分別對應8m/s、10m/s、12m/s。因來流速度受出口反壓影響,所以改變翼型迎角的過程中同時改變了出口截面積,流速會發生變化,所以來流速度很難在一次實驗中完全固定,低、中、高流速值僅僅是多次測量的平均結果。
由圖5可得:來流速度對升力系數影響不大,且線性擬合結果較好,從而在實驗中證明了升力系數是翼型的固有參數,與來流速度無關,符合薄翼型升力系數的相關理論。
4 誤差評定和分析
由圖5可以看出,實驗值和理論值之間存在較大誤差。下面分別從升力測量裝置的系統誤差和理論模型差異兩方面進行分析。
4.1 升力測量裝置導致的系統誤差
如上文所述彈簧測力裝置的讀數已用電子天平進行校定,得到用天平校準的升力值F0與升力計讀數F的關系,結果如圖6所示。
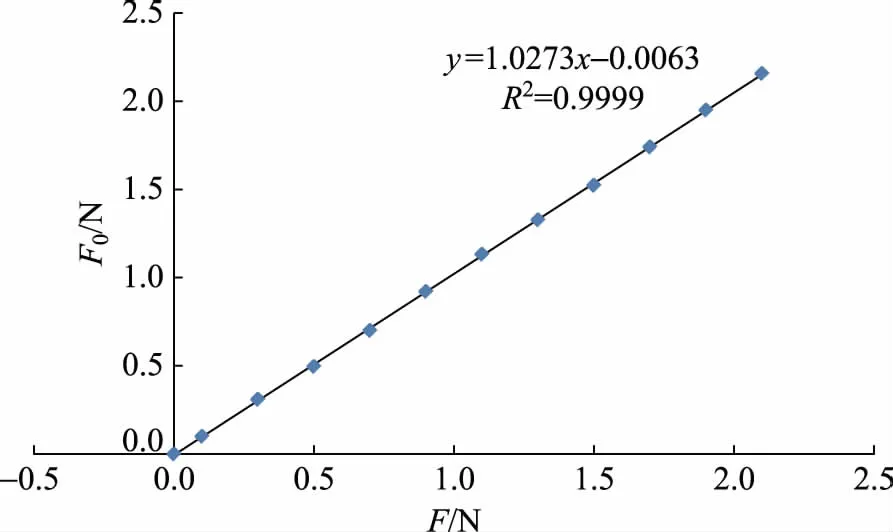
圖6 用電子天平對升力計校準的結果
對F0和F的測量結果做線性擬合,其結果為
F0=1.0273F-0.0065
(8)
由式(8)可得,校準所得的升力值F0和升力計讀數F雖存在一定偏差,但偏差程度不大,不足以導致升力系數測量值與理論值之間的較大誤差。
4.2 實驗模型和理論模型的差異導致誤差
薄翼型理論僅適用于流體受到的擾動可以進行線性化處理,忽略了湍流脈動的摻混損失,而簡易風洞由于自身結構簡單,湍流度較大,與理論模型存在較大的差異,這也是導致實驗誤差較大的主要原因。若取空氣密度ρ=1.2kg/m3,特征速度v=10m/s,粘性系數μ=18.1×10-6kg/(m·s),特征長度取風洞的特征尺寸b′=143mm,計算基于風洞尺寸給出的雷諾數:
(9)
簡易風洞可近似為管流,管流的湍流度T可通過雷諾數進行近似估計:
(10)
計算所得簡易風洞湍流度在5%左右,而科研用風洞的湍流度一般在1%以內[5]。湍流度過高使得流體在風洞中變得不穩定,在翼型的擾動下會造成氣流長距離的湍流脈動,湍流脈動對宏觀流動的作用效果不可忽略[6],導致測量誤差較大。此外,風機鼓出的空氣很難保證直勻流動,且在翼型的后半段存在邊界層的分離[3],風洞內部流動存在較大的三維性,摻混造成的損失和翼型后緣處的分離損失亦不可忽視。上述原因導致了簡易風洞中的實際翼型繞流偏離小擾動線性化理論的成立條件,使得實驗測量值小于理論值。
5 結語
利用簡易風洞和彈簧測力裝置設計了薄翼模型升力系數測量實驗。實驗測得的升力系數與迎角滿足線性關系,符合薄翼型理論結果。改變來流速度,數據的重復性較好,從而驗證了升力系數與來流速度無關的結論。由于簡易風洞并不能完全滿足薄翼型理論要求,會造成一些不可避免的誤差,但數據的總體趨勢和線性關系與理論是相符的。該簡易風洞實驗可用于教學,有助于學生理解抽象的空氣動力學知識,提高教學效果;學生也可自制翼型進一步研究不同翼型與升力系數的關系。
[1] 單鵬. 多維氣體動力學基礎[M]. 北京:北京航空航天大學出版社,2008.
[2] 陸瑞征, 黃麗菊. 讀《定性與半定量物理學》談工科物理教學改革[J]. 大學物理,1998, 17(4):37-39. LU Ruizheng, HUANG Liju.Teaching reform of engineering physics based on reading “Qualitative and Semi-quantitative Physics”[J]. College Physics, 1998, 17(4): 37-39. (in
Chinese)
[3] 錢翼稷. 空氣動力學[M]. 北京:北京航空航天大學出版社, 2004.
[4] 劉揚正, 錢仰德. 測定不同形狀物體空氣阻力系數的實驗[J]. 大學物理,2017, 36(3). LIU Yangzheng, QIAN Yangde. The experiment of measurement the air drag coefficient of different shape objects[J]. College Physics, 2017, 36(3). (in Chinese)
[5] 何克敏, 屠興. 低湍流度風洞及其設計[J]. 流體力學實驗與測量, 1988(2):11-18. HE Kemin, TU Xing. Design of low turbulence wind tunnel[J]. Experiments and Measurements in Fluid Mechanics, 1988(2): 11-18. (in Chinese)
[6] 王洪偉. 我所理解的流體力學[M]. 北京:國防工業出版社, 2014.

