鹽漬土溶出除鹽法中鹽運移的數學模型與特征

仇啟涵

（住化分析技術（上海）有限公司，上海 200436）

1 前言

2011年3月11日，日本發生的大地震對日本東北地區造成了大規模的損害。其中宮城縣僅在農業方面的損失總額就高達5450億日元，流失、冠水等受害面積約2.4萬ha（其中約85%為農田[1]）。主要涉及灌溉排水設施的損壞、地下水鹽污染等。其中又以海嘯引發的海水倒灌造成的農田土壤鹽漬化問題（土壤中的鹽濃度過高引起的植物無法生長及枯死的環境問題）最為嚴重。我國東部濱海地區，盡管沒有遭受地震海嘯等大規模自然災害，但由于地勢低平加之地下水長年過度開采，海水倒灌問題也十分突出，進而引發農田土壤的鹽漬化。在部分農田甚至經常可以看到地表析出結晶鹽的現象，對農業生產和生態環境造成了巨大的破壞[2]。

中日兩國上述地區由于淡水資源豐富以及灌溉排水條件較好，作為農田鹽漬化土壤治理的措施，溶出法除鹽技術（在農田地表灌水使土壤中的鹽分溶出，然后從排水口排出，如圖1）得到了廣泛應用。但對灌水量和冠水期的管理基本依靠經驗來決定，缺乏科學性依據，治理效果的定量評估也不明確[3]。尹建道[4]等對從鹽漬土地表灌水洗脫的規律和效果進行了探討，但未對鹽分從地表面溶出的過程進行研究。

本研究根據土壤中物質運移理論構建鹽溶出過程的數學模型，并通過室內模擬溶出除鹽實驗驗證其準確度，以期對現行除鹽工程的效果進行科學評估，進而提出效率更高的除鹽治理方案。

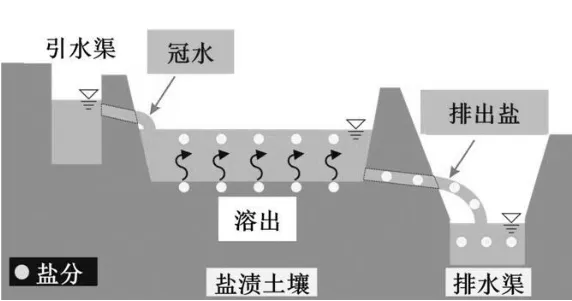
圖1 溶出除鹽法的原理

2 溶出除鹽法的鹽運移數學模型

土壤中表示鹽運動的擴散方程式如式①：

3 溶出法除鹽實驗概要

溶出法除鹽實驗在恒溫室（室溫22℃）進行，將采自鹽漬化農田的供試土壤（粉質黏土）以干密度1650kg/m3填充于丙烯酸樹脂圓柱（內半徑76mm，長100mm）后，在防止蒸發的同時利用鹽水通過毛細管作用從土柱下方使其飽和。之后，將帶有排水口（高3mm，直徑3mm）的圓柱與土柱連接，并將兩極傳感器（CS655，Campbell Scientific制）設置在土壤表面以下5mm、10mm、20mm、50mm及85mm的位置。同時，為了測定冠水的鹽濃度，在地表面0mm，地表上方10mm、30mm及50mm處設置四極傳感器（Sankei理化制）。根據冠水深度hw的變化適當調整冠水中傳感器的位置。

實驗步驟如下所述：

（1）在不擾動土壤的情況下，用膠頭滴管在土柱表面灌入一定量的淡水，靜置168小時。

（2）用2臺數據記錄器（Campbell Scientific和M.C.S產）以每1分鐘的頻率記錄下土壤和冠水中的溫度、鹽濃度C（Cl-質量/水的體積，kg/m3，以下簡稱“鹽濃度”）。

（3）冠水結束后，用滴管收集從排水口流出的鹽水和地表殘留水，通過電量滴定式鹽分分析儀（salmate-100，Asahi Life Science產）測定C。

（4）往土中鉛直插入鋼管（內徑20mm，長100mm），對不同深度的土壤進行采樣。

（5）完全干燥各樣品，計算其θ

4 實驗結果和模擬計算結果的比較

4.1 鹽溶出特征

續升高，各zw處的濃度差逐漸減小，48小時后可忽視濃度梯度的存在（dCw/dz ≒ 0）。hw=100mm時，72小時后zw=0mm與100mm間Cw的差隨時間變小。說明與深度無關冠水的鹽濃度梯度隨時間逐漸減小，冠水深度越低Cw達到相同的時間就越短。

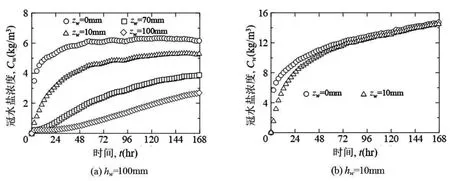
圖2 冠水鹽濃度的時間變化

圖3 （a）和（b）分別表示hw= 60mm和10mm時Cs的時間變化。兩者的Cs均隨時間減小，地表面以下20mm內的Cs下降很明顯，特別是在起始的48小時內。此外，越靠近土壤表面Cs的時間降低率越大。

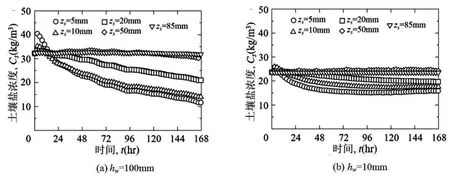
圖3 土壤鹽濃度的時間變化

4.2 溶出系數α

該數學模型中的溶出系數α是決定溶出量計算精確度的重要參數。Brutsaert[5]在研究水分從湖面向大氣中蒸發的速度時引入了通量系數。根據v = α（Cs_surf- Cw）從實驗結果反推計算出α的值。因很難精確測得地表鹽濃度Cs_surf和緊鄰地表面處的冠水鹽濃度，所以準確求得α值也比較困難。該模型通過將計算得到的Mt的時間變化與實驗測定結果進行曲線擬合來確定α的值。通過計算得出α的值為1.5×10-4～9.0×10-4m/h，與實驗中得到α的值的階（10-4m/h）相同。

4.3 數學模型的改良

式④和式⑤推導的前提條件是冠水中的鹽分分布達

由于Cw的時間性變化，Cs_surf和Mt也隨時間而變。此處假設Cs_surf和Cw即使發生空間變化式④和式⑤依然可用，以微小時間間隔（Δt=1min）計算Cs（z, t）、Cw（t）和Mt（t），其計算流程如圖4所示。

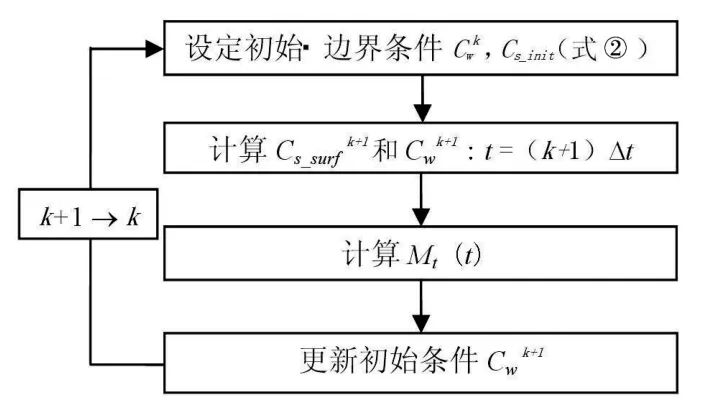
圖4 模型計算流程

4.4 模擬計算結果

因假設冠水中的鹽為完全混合狀態，故本文只對濃度梯度較小的hw=10mm時進行模擬計算。圖5分別表示地表面下zs=5mm、10mm、20mm和50mm處Cs的時間變化實驗值（圓點），舊模型（Cw=固定值）的計算值（虛線）和本模型的計算值（實線）。舊模型由于未考慮冠水中鹽濃度的增加，溶出過程被過大計算，各深度處Cs的減小迅速，168小時后zs=5mm和10mm的計算值分別約為其實驗值的1/3和1/2。而本模型的計算值與實驗值基本一致，但是zs=5mm和10mm處兩者的差比其他深度處的差大，推測是地表的土壤出現過飽和，是傳感器的輸出值與鹽濃度之間換算偏大造成的。因此，需要對傳感器在過飽和土壤中的輸出值與鹽濃度之間的函數進行再擬合，校正zs=5mm和10mm處的實驗值。

圖6表示hw=10mm時累積溶出量Mt的時間變化（圓點、虛線和實線的含義與圖5相同）。使用舊模型計算的話，Mt同樣出現結果偏大的現象，168小時后約為實驗結果的2.5倍。而使用式④和式⑤組合構成的模型進行的計算值則很好地再現了實驗值。

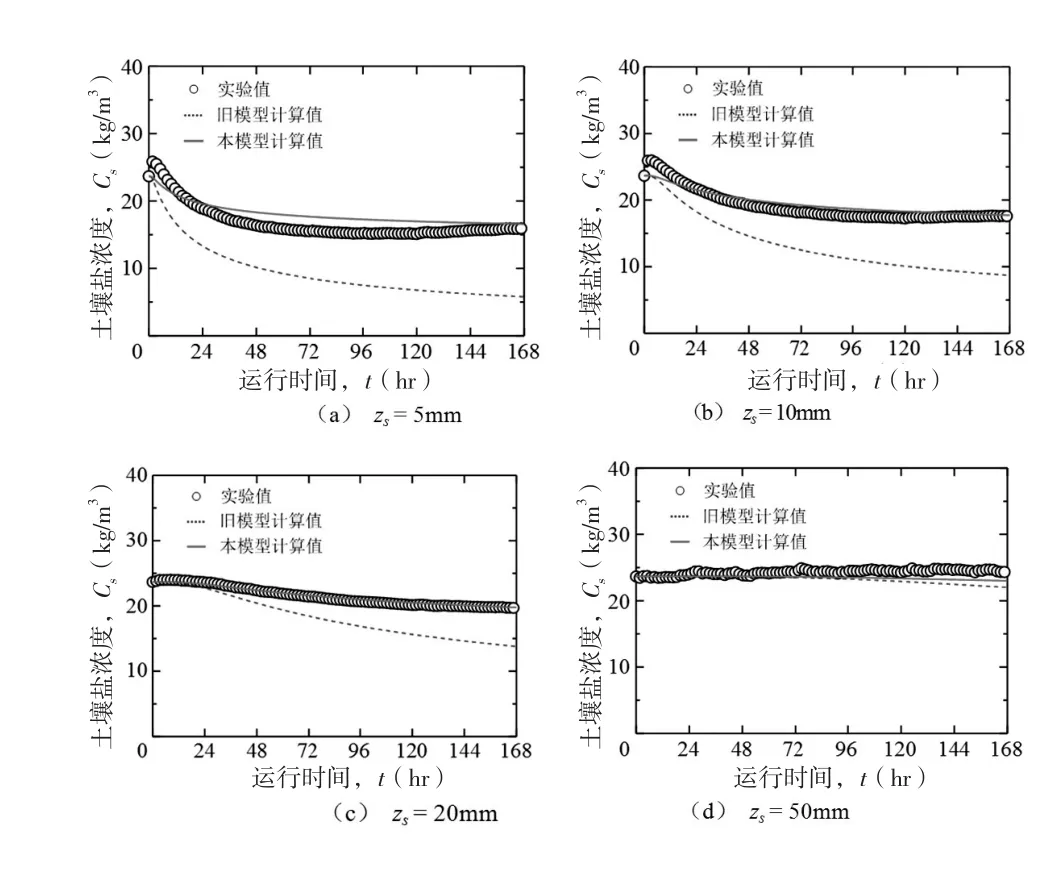
圖5 土壤中鹽濃度時間變化的實驗和計算結果的比較

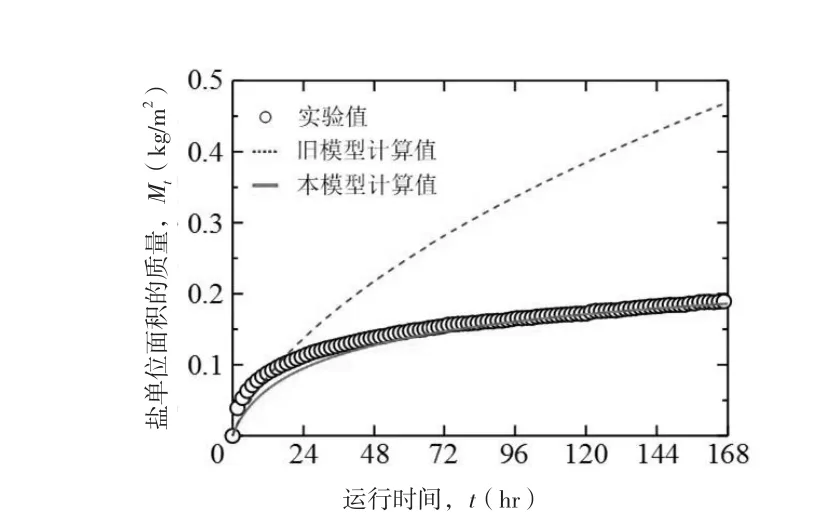
圖6 累積溶出量的實驗和計算結果的比較（hw=10mm）

5 不同冠水深的累積溶出量的評價

圖7表示hw=10～500mm不同冠水深時利用本模型計算的Mt的時間變化情況。此處以hw=10mm為基準，將各hw的Mt除以hw=10mm時的累積溶出量（Mt10）得到的值R（-），進行標準化。各hw的R均隨時間增大，但R的增大率逐漸減小。另外，hw越高R越大，168小時后hw=30mm、50mm、100mm、200mm和500mm的Mt分別約為Mt10的1.5倍、1.8倍、2.1倍、2.3倍和2.4倍。冠水深即使從hw=100mm增加到200mm，除鹽效率也僅提高了10%。由此可知，雖然冠水深越大除鹽效率越高，但所需的冠水期較長。從水的利用率和排水時間的角度來說，無需在地表灌溉100mm深以上的水。

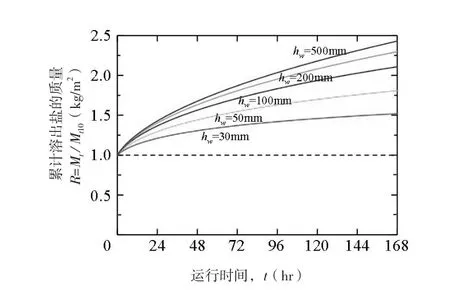
圖7 不同深度冠水時累積溶出量的計算結果

6 結論

本研究通過室內土柱實驗定量評價了鹽溶出特征。根據其結果，將鹽濃度伴隨溶出過程逐漸增加的因素考慮在內，對基于物質擴散方程式構建的鹽運移數學模型進行了改良，并驗證了改良模型的適用性。然后通過模擬計算討論了冠水深度對累積溶出量的影響。主要結論為：

（1）在鹽溶出過程中，越靠近地表面的土壤鹽濃度下降越顯著；

（2）冠水中在鉛直方向存在鹽濃度梯度，冠水深越小達到全域混合狀態的時間越短；

（3）溶出的鹽在冠水中達到均勻混合狀態時，只要準確求得溶出系數α，即可利用本模型大致預測溶出鹽量和土壤中鹽濃度的分布；

（4）冠水中不發生對流時，α的階為10-4m/h；

（5）冠水深度越大越促進鹽溶出，但100mm以上時促進效率增加很小。

在今后的研究中，將對實際農田鹽漬化土壤治理效果進行監測，并利用本模型計算驗證其在實際工程中的適用性，預測工程開展過程中土壤的水鹽運移，進一步提出高效的溶出法除鹽治理方案。

[1] 日本農林水產省. 平成23年度 糧食·農業·農村白皮書[R]. （2012-4-24）.

[2] 李怒云，龍懷玉.植樹造林與21世紀鹽漬土開發利用的關系[J].北京林業大學學報，2000，22（3）：99-100.

[3] 一般財團法人日本水土綜合研究所.農田的除鹽技術研討會報告書[R].2013， 63-73.

[4] 尹建道，姜志林，曹斌，楊勇，生原喜久雄.濱海鹽漬土脫鹽動態規律及其效果評價[J].南京林業大學學報，2002，26（4）：15-18.

[5] Brutsaert，W.Hydrology: An Introduction [M].Cambridge University Press， 2005．