基于可視化技術(shù)的曲面加工誤差分析及應(yīng)用*

邵 偉 彭 鵬 王 錯 周阿維

(① 西安理工大學(xué), 陜西 西安 710048；② 西安工程大學(xué), 陜西 西安 710048)

精密測量技術(shù)是推動國民經(jīng)濟發(fā)展的重要基礎(chǔ)技術(shù)之一，是先進制造中不可或缺的重要組成部分。隨著我國現(xiàn)代工業(yè)的發(fā)展，尤其是以數(shù)字制造為核心的先進制造技術(shù)的迅猛發(fā)展，對精密測量技術(shù)提出了新的要求：一方面要為先進制造技術(shù)擔負起質(zhì)量技術(shù)保證的重任；另一方面又不能單純?yōu)闄z測而檢測，還要為產(chǎn)品生產(chǎn)效益的提高貢獻力量[1-2]。隨著國民經(jīng)濟的迅猛發(fā)展，諸如汽車制造、船舶制造、航空航天、水利水電、武器裝備等領(lǐng)域?qū)Υ蟪叽鐪y量技術(shù)提出了越來越高的期望和要求[3-4]，尤其是對于重型、易變形的曲面工件檢測提出了越來越高的要求。因此，亟待研究曲面檢測新技術(shù)和檢測系統(tǒng)，以滿足目前市場的需求，保證機床的利用率及產(chǎn)品加工質(zhì)量。

而檢測數(shù)據(jù)處理完成后，進行檢測結(jié)果的應(yīng)用對在線檢測具有重要的意義。曲面檢測的目的是判斷所加工的曲面是否能滿足要求，主要是模型精度評定，即了解由測量數(shù)據(jù)所重構(gòu)的曲面模型和理論模型之間的誤差分布情況。對曲面工件進行評估后，可以檢查曲面工件的加工質(zhì)量，此外也可利用獲得的幾何尺寸信息對曲面工件生產(chǎn)工藝進行改進，使工件的廢品率降低，從而提高經(jīng)濟效益[5]。

曲面不像一般規(guī)則的幾何元素那樣，能用有限參數(shù)給出精確定義，對其加工精度的檢驗變得較為復(fù)雜。并且難以用精確的數(shù)學(xué)模型定量描述工件成形效果和加工工藝參數(shù)之間的關(guān)系。工業(yè)生產(chǎn)中，主要采用基于經(jīng)驗數(shù)據(jù)和反復(fù)試驗漸進的方法確定合適的加工成形工藝參數(shù)，成本高、周期長。因此，本文采用建立可視化的檢測誤差模型及表示方法并利用基于神經(jīng)網(wǎng)絡(luò)技術(shù)的專家系統(tǒng)獲得后續(xù)加工所需工藝參數(shù)，指導(dǎo)后續(xù)的數(shù)控加工，提高系統(tǒng)加工質(zhì)量和加工效率。

1 曲面檢測誤差可視化模型的建立

精度有較高要求的應(yīng)用中，檢測誤差分析常常是非常重要的。因此，針對曲面工件的加工精度，本文采用了基于檢測誤差模型(inspection error model，IEM)的誤差評估方法，即首先對工件進行測量后，由測量數(shù)據(jù)進一步得到重構(gòu)模型，將重構(gòu)模型與CAD模型進行配準，保證測量坐標系與設(shè)計坐標系一致，然后通過CAD模型上的測點和數(shù)控機床返回的檢測結(jié)果進行單點比較的方法進行單點的誤差計算，最終獲取模型間的檢測誤差信息，從而建立起檢測誤差模型，以便進行分析評估。

建立檢測誤差模型之前，首先要保證測量坐標系與設(shè)計坐標系一致，將理想模型(CAD模型)上的測點Ps(xs,ys,zs)與機床上返回的該點實測的位置Pm(xm,ym,zm)按式(1)進行計算，得出該點在法矢方向的距離定為當前的誤差值，正值表示該點的加工余量，而負值則表示該點過切。

(1)

本文建立的IEM是為了進行精度評價和誤差分析，并把它定義為：由曲面片集以及曲面誤差信息組成的模型。它完整地記錄了產(chǎn)品的幾何信息和檢測誤差信息(參見表1)。IEM是以配準后模型與CAD模型間的偏差為基礎(chǔ)建立起來的，其思想同樣可以應(yīng)用于逆向工程中的制造精度分析，重構(gòu)精度分析以及仿制精度分析。制造精度分析是指基于以CAD模型進行制造件加工精度的檢測，重構(gòu)精度分析是指以原型件為參考檢測重構(gòu)模型的過程，仿制精度分析是指原型件和復(fù)制件之間的定量比較。

表1 檢測誤差模型的內(nèi)涵

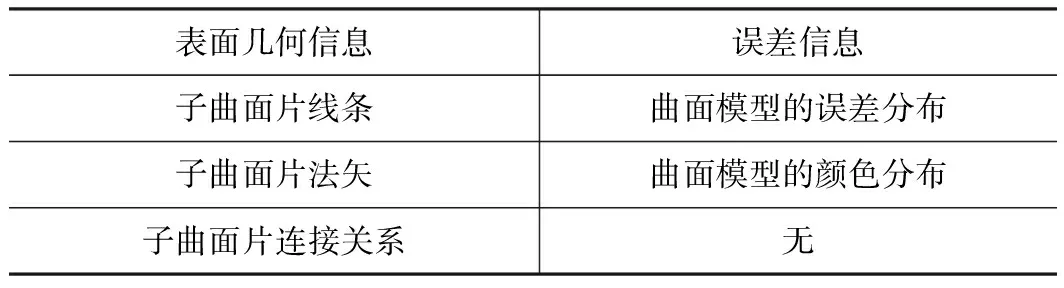
表面幾何信息誤差信息子曲面片線條曲面模型的誤差分布子曲面片法矢曲面模型的顏色分布子曲面片連接關(guān)系無

1.1 曲面檢測誤差可視化映射關(guān)系建立

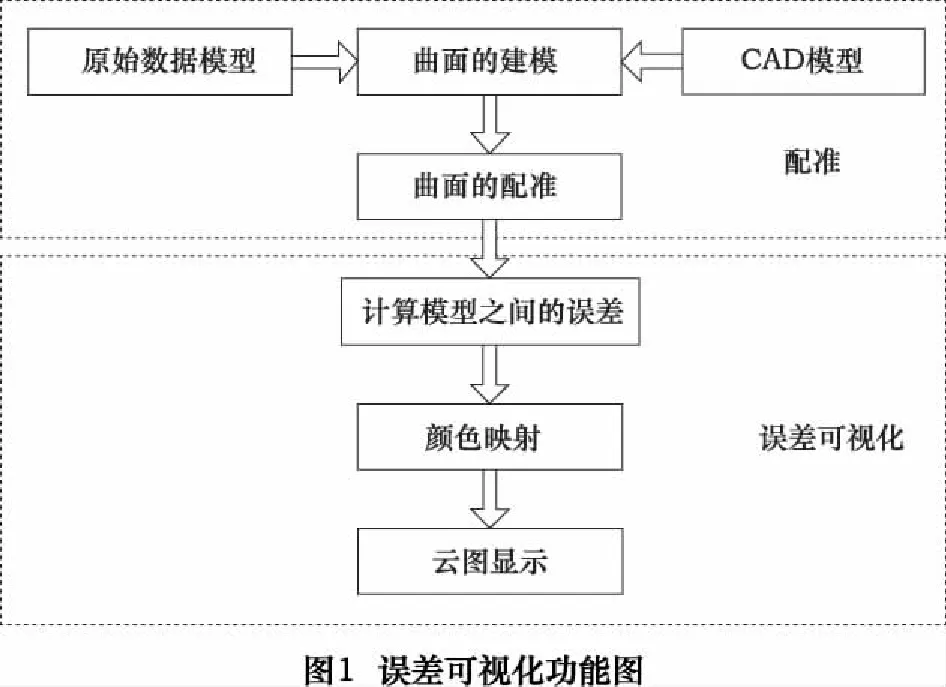
為了將曲面誤差結(jié)果直觀形象地反饋給用戶，通常將IEM結(jié)合數(shù)據(jù)可視化技術(shù)，建立了誤差與灰度值之間的映射關(guān)系，從而利用彩色云圖來表示重構(gòu)模型的誤差分布，為分析人員提供了一種可視化的分析手段。IEM的可視化包括以下幾個主要步驟：第一步是誤差數(shù)據(jù)生成；第二步是可視化映射，將誤差數(shù)據(jù)轉(zhuǎn)換為可供繪制的幾何圖素和屬性；第三步是將產(chǎn)生的幾何圖素和屬性轉(zhuǎn)換為可供顯示的圖像。IEM的可視化功能圖如圖1所示。下面先對顏色灰度值映射模型進行介紹。

1.1.1 RGB灰度值模型及其插值算法

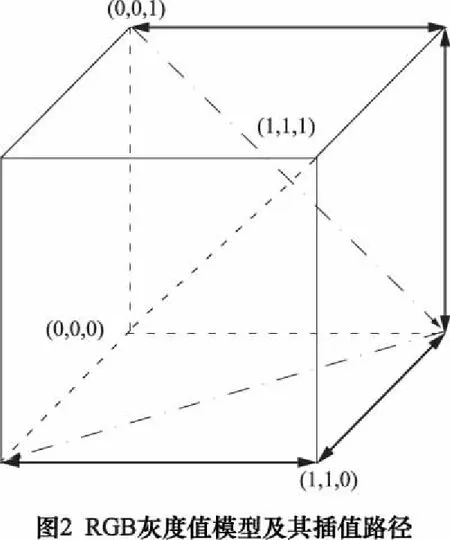
對應(yīng)不同的應(yīng)用場合有多種不同的RGB灰度值描述方法或稱RGB灰度值模型[6-7]，其中RGB灰度值模型通常用于圖形顯示器上，它采用直角坐標系，通常由R(紅)、G(綠)、B(藍)坐標軸定義的單位立方體來描述，如圖2所示。在正方體的主對角線上，各原色的量相等，產(chǎn)生由灰度值(0,0,0)到灰度值(1,1,1)的灰度變化。正方體的其他6個角點分別為(1,0,0)、(1,1,0)、(0,1,0)、(0,1,1)、(0,0,1)和(1,0,1)。

為了設(shè)計出無數(shù)種灰度值，使得給定變量x值和灰度值空間的某一子集一一對應(yīng)，可以采用灰度值插值的策略實現(xiàn)。在實際中，簡單的灰度值插值算法是三色線性灰度值插值，首先分別指定兩極值點和中值點的灰度值：RGBmin、RGBmax、RGBmd，其他的灰度值可通過式(2)的線性插值函數(shù)計算得到。

(2)

其中xmin、xmax分別為給定變量x的最小值、最大值。如插值路徑如圖2單點劃線所示，其插值函數(shù)為：

(3)

由于三色線性灰度值插值算法用到的灰度值較少，色彩比較單調(diào)。為得到對比鮮明，變化豐富的視覺效果，可采用更多色的插值策略。在此本文采用了一種五色線性灰度值插值算法，插值路徑如圖2中粗雙箭頭線條所示，則插值函數(shù)為：

(4)

1.2 曲面檢測誤差可視化實現(xiàn)過程

為了直觀地表示配準后模型與CAD模型間的誤差分布，首先將配準后模型中的重復(fù)點去掉；然后求取配準后模型到CAD模型間的誤差；再將誤差值同RGB灰度值映射起來；最后將模型的誤差分布用可視化的形式表示出來。其中主要技術(shù)是利用RGB灰度值技術(shù)將檢測誤差的數(shù)值點用對應(yīng)的RGB灰度值表示，對照RGB灰度值，研究人員就可以通過RGB灰度值視圖形象地看到檢測誤差分布情況。該RGB灰度值能從檢測誤差參數(shù)數(shù)據(jù)中自動查找出檢測誤差參數(shù)絕對值的最大值Ermax，并根據(jù)差值(Ermax-0)等分出若干檢測誤差區(qū)域，即進行顏色標號，然后遵循人們的習(xí)慣或用戶要求的對應(yīng)關(guān)系來實現(xiàn)檢測誤差與RGB灰度值的映射，并且令誤差為零處顯示為RGB(0,0,255)，最大誤差處顯示為RGB(255,0,0)，對于位于零與最大偏差之間的偏差，在其之間進行線性插值。把連續(xù)變化的檢測誤差人為地映射成階梯跳躍的RGB灰度值，計算出曲面檢測誤差值所對應(yīng)的RGB灰度值。這樣任意一個誤差與RGB灰度值映射表對應(yīng)起來，再將這個RGB灰度值映射到相應(yīng)的數(shù)據(jù)點，形成了誤差可視化云圖。

1.3 曲面檢測誤差可視化實現(xiàn)結(jié)果

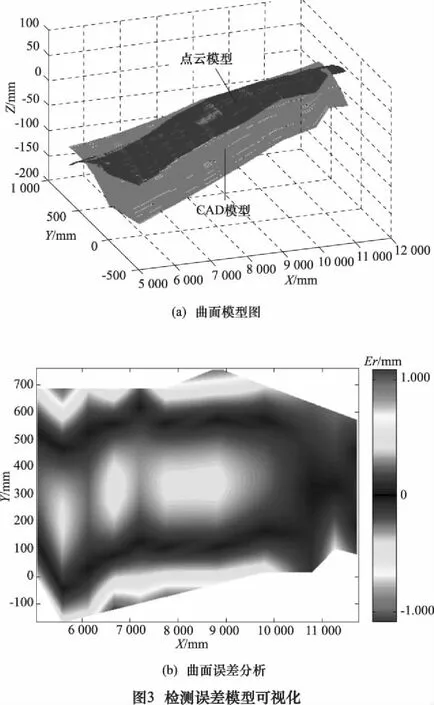
以某曲面為例，將配準后模型與CAD模型間的誤差分布用可視化云圖表示如圖3所示。圖3a為測量點云模型及其CAD模型，圖3b為誤差分布結(jié)果。

2 基于曲面檢測誤差模型的工藝參數(shù)改進

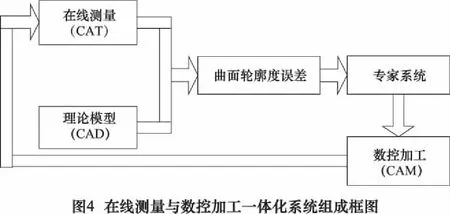
如圖4所示為大型曲面在線測量與數(shù)控加工一體化系統(tǒng)，即在曲面數(shù)控加工之后，進行在線測量，將測量結(jié)果與CAD模型數(shù)據(jù)進行比對，得到曲面檢測誤差模型，然后通過專家系統(tǒng)獲得數(shù)控加工所需工藝參數(shù)，指導(dǎo)數(shù)控加工的進行。該系統(tǒng)的一個重要的環(huán)節(jié)就是專家系統(tǒng)。

由于傳統(tǒng)專家系統(tǒng)只能處理顯性的表面的知識，推理能力弱，智能水平低等，而神經(jīng)網(wǎng)絡(luò)能高度逼近非線性系統(tǒng)并對復(fù)雜不確定系統(tǒng)具有自適應(yīng)和自學(xué)習(xí)能力[8]，因此采用具有多層前饋式誤差反向傳播(error back-propagation, BP)神經(jīng)網(wǎng)絡(luò)模型來進行大部分的知識獲取，其獲取的知識存儲在網(wǎng)絡(luò)的權(quán)值和閾值當中，并由網(wǎng)絡(luò)的并行計算而得到網(wǎng)絡(luò)的輸出結(jié)果。然后，將網(wǎng)絡(luò)輸出結(jié)果轉(zhuǎn)換成專家系統(tǒng)推理機能接受的形式，由專家系統(tǒng)的推理機得到數(shù)控加工的工藝參數(shù)。

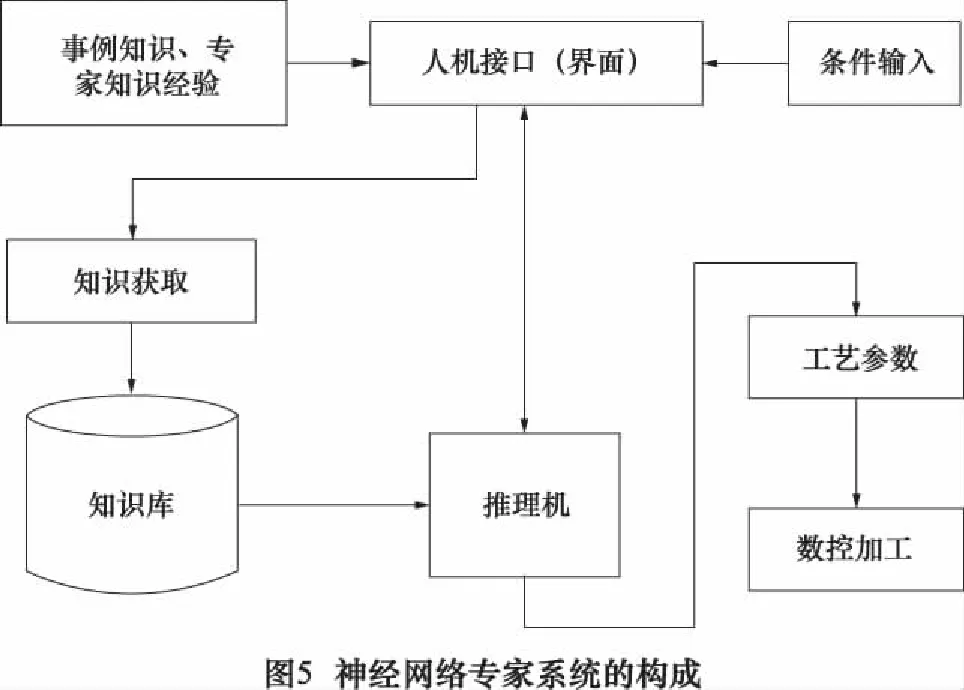
2.1 神經(jīng)網(wǎng)絡(luò)專家系統(tǒng)的構(gòu)成

如圖5所示，該神經(jīng)網(wǎng)絡(luò)專家系統(tǒng)主要由人機接口、知識獲取模塊、知識庫、推理機等部分組成[9-10]。知識庫是專家系統(tǒng)的核心。如果輸入曲面工件的幾何信息、厚度、物性參數(shù)等，系統(tǒng)根據(jù)知識庫中的實驗數(shù)據(jù)庫、專家知識、已建立的數(shù)學(xué)模型和算法等方法進行推理、判斷，就能得到合理的工藝參數(shù)。

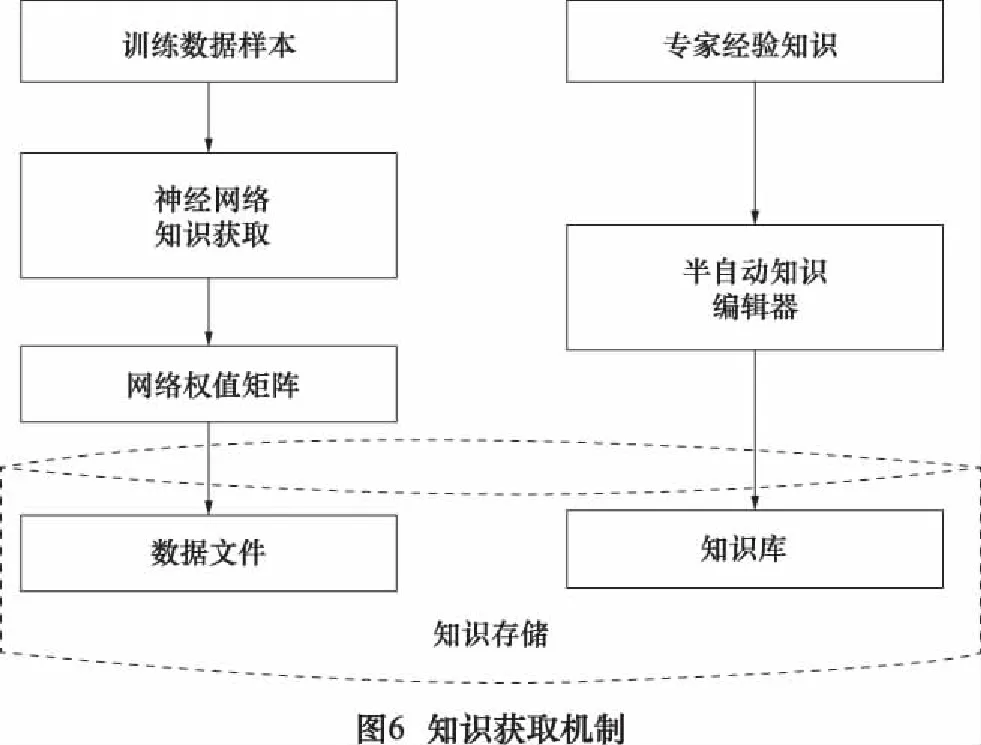
2.2 知識獲取

專家系統(tǒng)的核心是知識，因而在一個專家系統(tǒng)建造中，解決知識如何獲取是一個十分重要的課題[11]。在專家系統(tǒng)開發(fā)過程中，知識獲取是最難解決的一道工序，被認為是專家系統(tǒng)建造中的“瓶頸”問題。只有當知識獲取的手段自動化、智能化后，才可以說專家系統(tǒng)有了真正的智能。

本文涉及到兩部分知識的獲取：一是傳統(tǒng)描述性知識獲取；二是從實例樣本中獲取隱含性知識。第一部分采用半自動化的知識獲取工具，領(lǐng)域?qū)＜铱梢愿鶕?jù)界面向?qū)В恍枰R工程師幫助，方便地將領(lǐng)域知識及經(jīng)驗錄入到知識庫中；第二部分用人工神經(jīng)網(wǎng)絡(luò)進行知識的自動獲取。通過神經(jīng)網(wǎng)絡(luò)對樣本數(shù)據(jù)的學(xué)習(xí)，將其中隱含的知識存儲到整個網(wǎng)絡(luò)中，并用數(shù)據(jù)文件的形式保存網(wǎng)絡(luò)的權(quán)值和閾值。此種知識獲取機制的結(jié)構(gòu)如圖6所示。

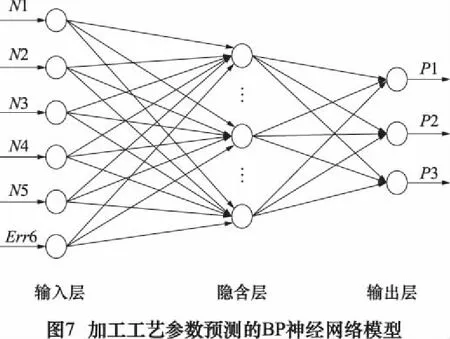
大部分的知識獲取可采用BP網(wǎng)絡(luò)模型來進行，BP網(wǎng)絡(luò)由輸入層、輸出層和若干隱含層構(gòu)成，每層由若干個結(jié)點組成，每一個結(jié)點表示一個神經(jīng)元，上層結(jié)點與下層結(jié)點之間通過權(quán)連接，同一層結(jié)點之間沒有聯(lián)系。由于BP神經(jīng)網(wǎng)絡(luò)具有逼近任意連續(xù)函數(shù)和非線性映射的能力，因此在神經(jīng)網(wǎng)絡(luò)研究領(lǐng)域中得到了廣泛的應(yīng)用，其結(jié)構(gòu)簡單，可操作性強，能模擬任意的非線性輸入輸出關(guān)系。利用BP網(wǎng)絡(luò)獲取知識的基本思想是：首先提供足夠數(shù)量的學(xué)習(xí)樣本供網(wǎng)絡(luò)訓(xùn)練，通過調(diào)整網(wǎng)絡(luò)權(quán)值使得輸入信息通過輸入層經(jīng)隱含層逐層處理并計算出的網(wǎng)絡(luò)輸出盡可能的接近期望輸出，通過訓(xùn)練，將網(wǎng)絡(luò)的權(quán)值調(diào)整到合適的值，使得對所有樣本都能夠得到期望輸出，這時，網(wǎng)絡(luò)的訓(xùn)練就結(jié)束了，就可以用該網(wǎng)絡(luò)來進行知識的自動獲取了。BP網(wǎng)絡(luò)訓(xùn)練采用的學(xué)習(xí)樣本由輸入和期望輸出兩部分數(shù)據(jù)組成，如圖7所示。網(wǎng)絡(luò)的輸入是曲面工件的物性參數(shù)中的彈性模量N1、泊松比N2、屈服強度N3和硬化指數(shù)N4，以及工件厚度N5、工件曲面的檢測誤差值Err6。該網(wǎng)絡(luò)的期望輸出是對應(yīng)的數(shù)控加工工藝參數(shù)，以噴丸成型加工為例，其工藝參數(shù)為彈丸流量P1、噴射氣壓值P2和機床速度P3。

2.3 推理機制

推理機實質(zhì)上是計算機的一組程序，目的是用于控制、協(xié)調(diào)整個專家系統(tǒng)的工作。它根據(jù)當前的輸入數(shù)據(jù)或信息，再利用知識庫中的知識，按一定的推理策略去處理、解決當前的問題。

在該系統(tǒng)中，采用的推理策略為正向推理，系統(tǒng)根據(jù)輸入的數(shù)據(jù)，在知識庫中找到神經(jīng)網(wǎng)絡(luò)的權(quán)值矩陣的有關(guān)數(shù)據(jù)。然后，計算神經(jīng)網(wǎng)絡(luò)的輸出，根據(jù)此輸出進行數(shù)控加工工藝參數(shù)調(diào)整的指導(dǎo)，最后給出推理結(jié)果。具體推理步驟如下：

(1)將輸入數(shù)據(jù)加到神經(jīng)網(wǎng)絡(luò)輸入層的各個神經(jīng)元。

(2)按照已確定的網(wǎng)絡(luò)傳遞特性和輸入數(shù)據(jù)計算輸入層各神經(jīng)元的輸出，并把它們作為隱含層單元的輸入。

(3)再分別計算隱含層神經(jīng)元及輸出層神經(jīng)元的輸出。

運用神經(jīng)網(wǎng)絡(luò)算法，可以精確地計算出數(shù)控加工的工藝參數(shù)值，從而為進一步的加工提供了依據(jù)。

3 實驗分析

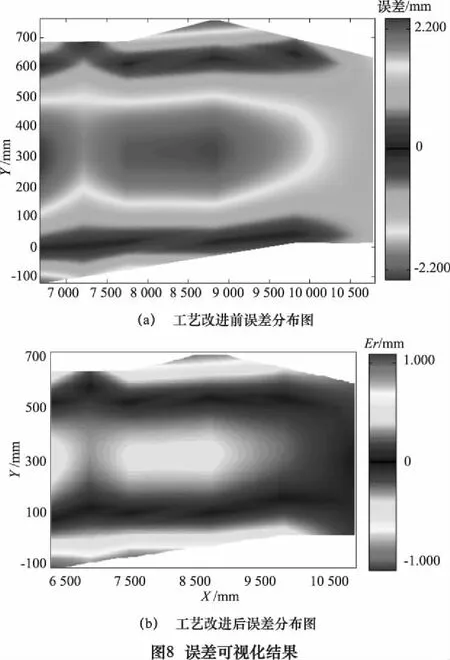
以某曲面壁板零件加工為例，對壁板曲面進行檢測的誤差結(jié)果如圖8a所示；然后，通過專家系統(tǒng)獲得加工所需工藝參數(shù)，指導(dǎo)加工，可得到修改后的曲面檢測的誤差結(jié)果如圖8b所示。由圖8可知，根據(jù)曲面在線檢測誤差對數(shù)控加工工藝參數(shù)進行改進，再加工得到的曲面與理論模型的誤差明顯減小，這樣使工件的廢品率降低，從而提高生產(chǎn)效率和經(jīng)濟效益。

4 結(jié)語

本文對曲面檢測誤差模型的建立和表示方法進行了研究，首先建立了檢測誤差模型，實現(xiàn)了檢測誤差的數(shù)字化傳遞，然后用可視化云圖對誤差結(jié)果進行直觀的表示，并對誤差結(jié)果進行分析，最后通過基于BP人工神經(jīng)網(wǎng)絡(luò)的專家系統(tǒng)獲得數(shù)控加工所需工藝參數(shù)值，從而為進一步的數(shù)控加工提供了指導(dǎo)依據(jù)，有效地提高了加工精度和加工效率。

[1]裘祖榮，石照耀，李巖.機械制造領(lǐng)域測量技術(shù)的發(fā)展研究[J].機械工程學(xué)報，2010，46(14)：1-11.

[2]陳巧巧.淺談數(shù)控機床在線測量技術(shù)[J].計量與測試技術(shù), 2012, 39(6):37-39.

[3]Savio E, Chiffre LD,Schmitt R.Metrology of freeform shaped parts[J].CIRP Annals.Manufacturing Technology,2007, 56(2):810-835.

[4]鄭聯(lián)語, 朱緒勝, 姜麗萍.大尺寸測量技術(shù)在航空制造業(yè)中的應(yīng)用及關(guān)鍵技術(shù)[J].航空制造技術(shù), 2013, 427(7):36-41.

[5]孫郅佶，安晨輝，楊旭，等.超精密機床主軸回轉(zhuǎn)誤差在線測試與評價技術(shù)[J].制造技術(shù)與機床, 2015(9):118-123.

[6]項志鋼.計算機圖形學(xué)[M].北京：清華大學(xué)出版社，2008.

[7]陳敏雅, 金旭東.淺談計算機圖形學(xué)與圖形圖像處理技術(shù)[J].長春理工大學(xué)學(xué)報, 2011(1):142-143,150.

[8]Joseph C Giarratano, Gary D Riley. 專家系統(tǒng):原理與編程:principles and programming [M].北京：機械工業(yè)出版社，2006.

[9]別秀德.BP神經(jīng)網(wǎng)絡(luò)應(yīng)用研究[J].智慧工廠, 2016(1):97-102.

[10]Bangalore P, Tjernberg L B.An artificial neural network approach for early fault detection of gearbox bearings[J].IEEE Transactions on Smart Grid, 2017, 6(2):980-987.

[11]馮定.神經(jīng)網(wǎng)絡(luò)專家系統(tǒng)[M].北京：科學(xué)出版社，2006.