高速艦船的運動模型適用性分析及海浪中的操縱仿真試驗

孫 健，陳永冰，周 崗，徐務農

(1. 海軍工程大學 電氣工程學院，湖北 武漢 430033；2. 海軍九〇二廠，上海 200083)

0 引 言

船舶運動模型的建立是船舶控制的基礎工作，對于控制方法的研究以及自動舵的研制和陸基條件下的檢測具有重要意義。中低速船運動過程中橫搖角較小，對首搖運動的耦合作用可忽略不計，進行仿真試驗時可只考慮包括橫蕩、縱蕩、首搖的平面運動三自由度模型。然而高速艦船的操縱性和普通中低速船較為不同，回轉運動中橫搖角的幅值較大，對首搖運動的回轉力矩產生一定的影響，使用三自由度模型進行仿真會產生較大的誤差。為了全面精確地進行船舶操縱運動仿真，必須建立四自由度運動模型。目前，考慮橫搖耦合的四自由度運動還沒有一個統一的數學模型，常見的有孫景浩提出的和平野提出的兩類模型[1]。本文使用平野給出的四自由度模型對DTMB5415船進行操縱運動仿真試驗，將2次仿真結果與水池試驗數據進行對比及誤差分析,驗證了該數學模型的適用性。

另一方面，現實中船舶航行時會受到風浪流等環境干擾的影響，其中波浪干擾最為復雜，干擾作用也最為明顯。波浪干擾不僅會使船舶的航跡產生漂移，還會引起搖蕩運動，其中對橫搖的影響尤為明顯[4]。對于波浪中的船舶操縱性能，Kijima[2]建立了1階及2階波浪力影響下的四自由度船舶運動模型，Yasukawa[3]對S175船進行了波浪中的自航模試驗及基于MMG的仿真回轉試驗。本文在上述研究的基礎上建立了海浪干擾力模型，對DTMB5415船在隨機波浪干擾下的運動進行仿真，分析了波浪對高速艦船操縱運動的影響。

1 靜水中的船舶運動模型

三自由度的MMG模型如下所示：

式中：下標H，P，R，W分別為船體水動力，槳的推進力，舵力及波浪干擾力。

平野模型在三自由度MMG模型的基礎上給出了橫搖模型，并且考慮了橫搖耦合對橫向流體動力YH及NH的影響，將這2項分解為受到橫搖耦合影響和不受橫搖影響的2項，即

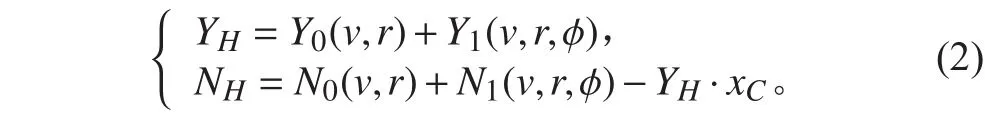
式中：Y0，N0為橫搖角為0時的流體動力及力矩，依照三自由度模型的估算方法進行計算；Y1，N1即為橫搖耦合造成的附加力和力矩，由平野的研究有：

平野給出橫搖自由度的動力學方程如下式：

式中：LH由橫搖阻尼力矩、恢復力矩及橫向流體動力YH對x軸的力矩這3項組成，如下式所示：

橫搖阻尼力矩當橫搖角在10°以內時，可采用線性橫搖阻尼力矩的形式進行計算，即，為線性阻尼系數。恢復力矩中的為穩性力臂，有，其中GM為船舶初穩性高。橫向流體動力YH對x軸的力矩反映了橫搖對于平面運動的耦合作用。

2 海浪干擾模型的建立

理想流體中，船舶在波浪中的運動可以看作是高頻運動和低頻運動的疊加[5]。1階波浪力即高頻波浪干擾力，主要引發船舶的搖蕩運動，而對于縱蕩、橫蕩和首搖運動的影響較小。2階波浪力即波浪漂移力，與波高的平方成正比。波浪漂移力是非線性的，具有慢時變特性，對于船舶航向航跡變化的影響較大。綜上，本文對于平面運動的3個自由度方程只考慮2階波浪漂移力的影響而對于橫搖方程僅考慮1階波浪干擾力的影響[6]。

2.1 不規則波的數學描述

不規則波主要是采用線性疊加原理來進行描述，即可以將不規則波的波面看作由一系列不同頻率、波數、波幅以及初相位角和傳播方向的規則波疊加而成。通過余弦序列權重系數法可以由波譜密度得到波面歷時值：

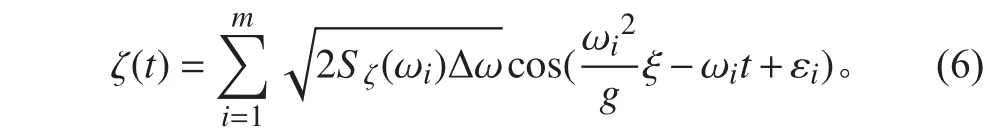
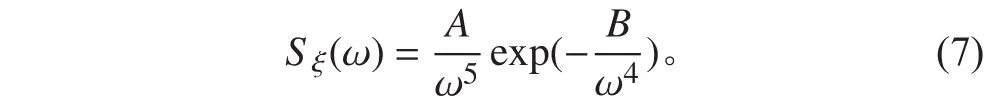
圖 1 海浪波譜密度曲線Fig. 1 The spectrum curve of wave

2.2 波浪干擾力的計算

對于1階波浪干擾力，目前有2種較為常用的方法，一種是應用長峰波隨機海浪疊加原理求解，另一種是通過脈沖響應求解。本文使用第1種方法。由于1階波浪力對船舶平面運動的影響很小，故只對橫搖這一個運動模態下的干擾力進行計算：

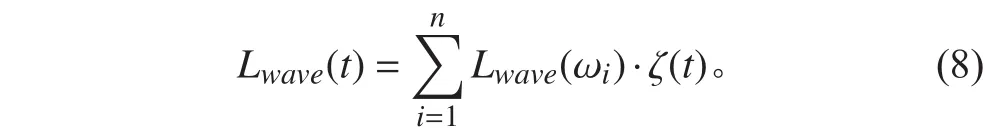
2.3 波浪漂移力及力矩的計算

由于不規則波可以看作是各種頻率的規則波的疊加，可以通過疊加的方法計算不規則波的波浪漂移力。

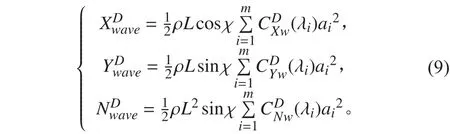
式中：ai為波幅，可由波譜密度函數得到；χ為波浪遭遇角，考慮深水波時，；，，為實驗系數，可由Daidola根據English的船模試驗得到的回歸公式求得。

3 操縱仿真試驗

本文以DTMB5415驅逐艦作為研究對象進行仿真試驗。該船主要參數如表1所示[7]。

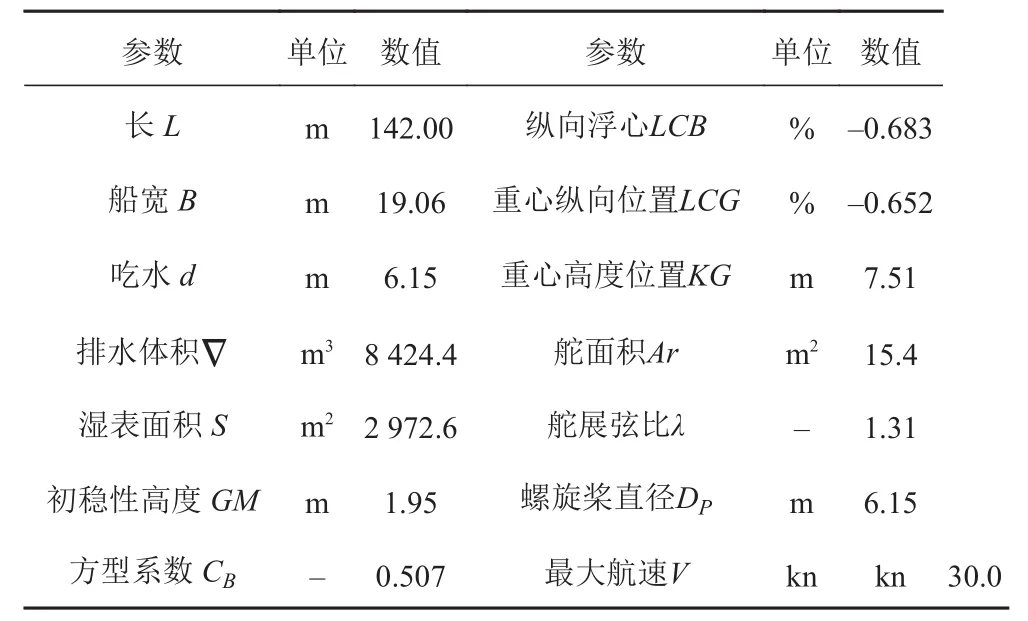
表 1 DTMB5415船主要參數Tab. 1 The major parameters of ship DTMB5415

使用Simulink作為仿真平臺，將船舶運動模型分為推進系統模型、舵系統模型、船體水動力模型及波浪干擾力模型、波浪漂移力模型等幾個模塊，仿真原理框圖如圖2所示。

圖 2 仿真原理框圖Fig. 2 The block diagram of simulation

3.1 不同舵角下的船舶回轉運動仿真

靜水中對DTMB5415船分別在不考慮橫搖運動及考慮橫搖運動耦合2種情況下進行回轉操縱仿真試驗并且將2次仿真實驗結果與水池試驗數據進行對比。航速設定為最大航速30 kn，轉舵速率為9(°)/s，指令舵角分別設定為35°和25°。仿真實驗結果如下：

回轉過程中橫搖角的變化如圖3（d）及圖4（d）所示，船舶回轉過程中的橫搖角呈周期性變化規律。轉舵階段由于作用于船舶重心的橫向慣性力指向內側，作用于舵面積中心的橫向舵力指向外側，故產生短時間的船舶內傾。過渡階段，伴隨角速度及漂角的增大，船體慣性力變化為指向外側，與橫向舵力方向相同，但由于其數值相比舵力要大得多，船舶會產生外傾。定常回轉階段橫搖角趨于穩定。當船舶進入定常回轉階段，橫搖角的變化率，橫向加速度以及首搖角加速度均為0。忽略舵力的影響，可近似認為作用于船體的慣性力引起了船舶的橫傾外力矩。

由圖3和圖4可以看出，橫搖耦合對DTMB5415船的回轉運動仿真結果有較為明顯的影響。為驗證仿真實驗的可行性，以進距（AD）和戰術直徑（TD）作為回轉運動主要特征參數，將水池試驗[7]得到的數據均值與2次仿真實驗的結果進行比較并進行誤差分析。比較結果如表2所示。

表 2 水池試驗與兩次仿真實驗結果Tab. 2 Results of pool test and two simulation experiments

由表2可以看出，橫搖運動對于首搖運動的影響主要是增大了船體水動力對于Z軸的回轉力矩，從而增大了回轉角速度，減小了回轉半徑。不考慮橫搖耦合的情況下仿真實驗相對水池試驗的誤差超過了10%。考慮橫搖運動耦合的影響，仿真實驗相對水池試驗的誤差下降到5%以內，上述對比結果反映了橫搖耦合對高速艦船回轉性的影響，同時驗證了仿真實驗方法的可行性。

圖 3 35°舵角下 DTMB5415 船的回轉運動仿真圖Fig. 3 The simulation diagram of DTMB5415 under the rudder angle of 35°

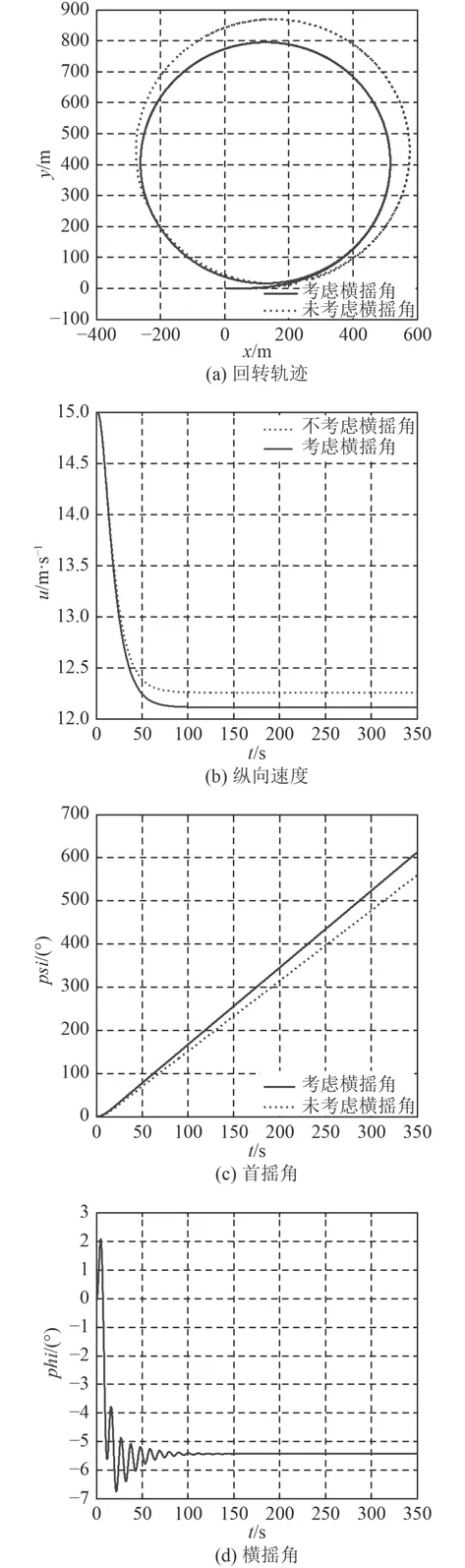
圖 4 25°舵角下 DTMB5415 船的回轉運動仿真圖Fig. 4 The simulation diagram of DTMB5415 under the rudder angle of 25°

3.2 波浪干擾下的船舶回轉運動仿真

在上述仿真實驗的基礎上加上波浪干擾作用，對DTMB5415船進行波浪中的直航運動仿真。設定航速30 kn，初始遭遇角 χ為 90°，有義波高分別為 4 m和5 m，船舶直航時橫搖角的變化曲線如圖5所示。

圖 5 波浪干擾下 DTMB5415 船的橫搖角變化曲線Fig. 5 The curve of rolling angle of ship DTMB5415 under the wave interference

如圖5所示，直航時橫搖角的變化幅度隨時間變化，這是由于波浪漂移力的作用使首搖角發生偏移，導致波浪遭遇角的變化，使得波浪對船體干擾的幅度大小產生變化。另外，由于初始階段船舶的非線性阻力較小，可以看出橫搖幅值較大。比較圖5（a）和圖5（b）可以看出有義波高為較大時，橫搖角幅度明顯增大。

對DTMB5415船進行波浪中的回轉運動仿真。設定有義波高4 m，初始航速30 kn，舵角35°，舵速為9(°)/s，初始遭遇角χ分別為45°和90°。船舶回轉運動軌跡及橫搖角變化曲線如圖6所示。

由圖6可見，在波高4 m，不同初始遭遇角的不規則波浪中，由于船體水動力、舵力以及1階波浪干擾力的作用，船舶在穩定橫搖角周圍進行幅值不定的擺動。其橫搖幅值隨遭遇角的變化而改變，可以看出，橫浪中的橫搖幅值較首尾斜浪中的橫搖幅值要大。另一方面，可以看出船舶由于波浪漂移力的作用，回轉軌跡都產生了明顯的偏移,偏移方向由初始遭遇角決定。

4 結 語

圖 6 波浪干擾下 DTMB5415 船回轉運動仿真圖Fig. 6 The simulation diagram of ship DTMB5415 under the wave interference

本文通過Matlab對DTMB5415船分別進行了三自由度運動建模以及加入橫搖的四自由度運動建模，通過仿真操縱實驗得到了回轉運動過程中的縱向速度、首搖角、橫搖角等運動狀態量，分析了回轉運動中橫搖角的變化規律，可以看出對于高速艦船，大舵角回轉時的穩定橫搖角可以達到5°以上。另一方面，橫搖運動耦合作用增大了繞Z軸的回轉力矩。通過將不同舵角下加橫搖、不加橫搖2次仿真的回轉圈的特征參數與水池試驗結果進行對比及誤差分析，可以看出：由于回轉過程中較大的橫搖角，三自由度運動方程已不能夠滿足實用的要求，加橫搖運動模型相對于水池試驗結果的誤差比不加橫搖的三自由度運動模型大大降低。

在上述模型的基礎上疊加波浪力和力矩，模擬不同初始遭遇角的波浪干擾下的船舶直航運動和回轉操縱運動，對比分析了不同運動狀態下船舶橫搖角和回轉圈的變化規律，為進一步研究高速艦船的操縱性及運動控制打下了基礎。

[1]賈欣樂, 楊鹽生.艦船運動數學模型 [M].大連: 大連海事大學出版社, 1999.

[2]KIJIMA K, FURUKAWA Y. Ship maneuvering performance in waves[C]//3rd International Stability Workshop, 1997.

[3]YASUKAWA H, et al. Simulations of ship maneuvering in waves(1st report: turning motion)[J]. Journal of the Ship and Ocean Engineering Society of Japan, 2006 (4): 163–170.

[4]尹茜, 陳紅衛. 隨機海浪下船舶搖蕩的計算機仿真[J]. 微電子學與計算機. 2007, 24 (6): 191–193.

YIN Qian, CHEN Hong-wei. The simulation of ship’s motion on random wave [J]. Microelectronics and Computer, 2007,24(6): 191–193.

[5]NONAKAK. On the maneuvering motion of a ship in waves [J].Transaction of the West–Japan Society of Naval Architects,1991(80): 73–86.

[6]陶堯森. 船舶的耐波性[M]. 上海: 上海交通大學出版社, 1985.

[7]SERGE T, FRANS V W, RINK H. Manoeuvring and seakeeping tests for 5415M [R]. Maritime Research Institute(MARIN), Wageningen/Delft University of Technology, The Netherlands Maritime Research Institute (MARIN),Wageningen.

[8]陳寧, 龔蘇斌. 船舶回轉運動仿真[J]. 艦船科學技術. 2013,35(3): 9–14.

CHEN Ning, GONG Su-bin. The research on the ship turning movement based on Simulink[J]. Ship Science and Technology.2013, 35(3): 9–14.