多通道模擬信息轉換器壓縮采樣實驗平臺開發

郇 浩

(1. 北京理工大學 信息與電子學院， 北京 100081; 2. 北京市分數域信號與系統重點實驗室， 北京 100081)

開展超寬帶信號采樣與處理技術的研究并做好相應的技術儲備，對我國航天微波成像和遙感測控技術的發展具有重要的意義和應用價值。微波成像和測控通信系統大多是基于擴頻的傳輸體制，擴頻信號所調制的信號在帶寬上表現出大量的信息冗余，壓縮感知技術便是利用這一先驗信息實現降采樣處理。2004年，Candes等[1]提出壓縮感知(compressive sensing，CS)理論，Donoho[2]從數學上解決了該理論的相關問題，為稀疏信號的亞奈奎斯特采樣奠定了理論基礎。Richard G. Baraniuk 研究團隊在DARPA 資助下開展了模擬信息轉換(analog-to-information converter， AIC)方法研究，并于2006年提出隨機解調結構[3]，該方案對AIC的發展起了很大的推動作用[4-6]。AIC結構由高速偽隨機解調器、低通濾波器和低速ADC 組成，它通過一個高速偽隨機乘法器，有效降低后端AD速率并減少數據率和存儲單元。隨后Yonina C. Eldar研究團隊開展了針對信號模型是稀疏多頻帶信號的采樣結構的研究，并將該采樣結構命名為調制寬帶轉換器(modulated wideband converter， MWC)[7-9]。西安電子科學技術大學的石光明針對超寬帶信號處理中面臨的采樣率過高的問題，提出一種基于壓縮感知理論的超寬帶回波信號采樣系統[10]，用于檢測超寬帶回波信號。中科院電子所研制出CS-SFGPR系統[11]，提出了一種基于壓縮感知的頻率步進雷達成像算法，通過少量的隨機采樣數據實現了測量信號的重建。

針對傳統AIC結構量化誤差大、信噪比嚴重損失等難題，本文提出了基于連續波模擬混頻壓縮采樣技術、多通道壓縮采樣相干積累技術的超寬帶信號壓縮采樣實驗平臺設計方法，推動壓縮采樣技術在超寬帶雷達、通信等技術領域的工程應用。

1 多路模擬信息轉換器的設計方案

本文所提出的多路模擬信息轉換器由多組基于chirp信號混頻的AIC隨機解調系統和加法器構成。輸入信號經功分器分別輸入至K個AIC隨機解調通道的信號輸入端口；經混頻、濾波、采集和信號重構之后，由加法器對K條路的重構信號進行相加輸出，實現結構如圖1所示。

圖1 多路模擬信息轉換器系統方案接收端結構圖

為了克服偽隨機序列的時鐘抖動和孔徑效應，混頻序列由原來的PN序列改為chirp信號，保證chirp信號帶寬與PN序列碼速率一致，利用chirp信號和PN序列擁有相類似的擴頻特征，實現對原始信號的混頻。由于chirp信號自身沒有陡峭的跳變沿，因此受到時鐘抖動和孔徑效應的影響大大降低。所采取的技術方案步驟如下:

步驟一，調節用于混頻的chirp信號，令所述chirp信號的持續時間與模擬信號x(t)的持續時間一致，所述chirp信號的調頻率為B/T；其中，B為信號帶寬，T為模擬信號x(t)的持續時間；

步驟二，將模擬信號x(t)與chirp信號進行混頻，混頻過程用數學表達式表示為y1=C1x，其中，C1為常數矩陣，其對角線元素為調頻率為B/T的chirp序列，其余元素為0；

步驟四，根據壓縮感知的正交匹配算法[12](orthogonal matching pursuit， OMP)，利用所述1/r倍欠采樣信號對所述模擬信號進行重構，得到第一路重構信號x1；

步驟五，考慮第k=2，…，K路重構信號，將步驟一中所述chirp信號的調頻率設置為(1+k/K)B/T。基于修改調頻率后的chirp信號重復步驟一至步驟四的過程，得到第k路重構信號為xk，k=2，…，K；

步驟六，將上述K路重構信號進行平均相加，即(x1+x2+…+xK)/K，利用最大峰值搜索方式得到重構信號的最大的多個峰值位置和能量取值，從而實現目標信號的重構。

2 多路模擬信息轉換器重構算法設計

2.1 傳統AIC結構存在的時鐘抖動和孔徑效應

在AIC采樣系統中，由于采用了低速ADC，因此ADC本身的時鐘抖動與孔徑效應通常可以忽略不計。然而，AIC系統所使用的PN混頻序列需要具備與信號相同的帶寬，反映到時域表現為PN序列的碼片速率與對信號進行奈奎斯特采樣所需的脈沖速率基本一致。因此，混頻PN序列的上升沿與下降沿也會受到時鐘抖動與孔徑效應的干擾，間接影響AIC系統的采樣精度，如圖2所示。

在AIC系統中，時鐘抖動會使實際PN序列中的一部分碼片的正負與理想值相反。這會使得信號在重構中出現錯誤。孔徑效應則會使得信號的采樣值被采樣點兩邊的信息干擾。綜合上述2個因素的影響，基于PN混頻序列的AIC結構在高速模式下會增加量化噪聲，損失信號分辨動態范圍。

chirp連續波信號相比PN序列沒有陡峭的跳變沿，對時鐘抖動、孔徑效應不敏感，并且能夠達到相同帶寬的混頻效果。基于chirp混頻序列的隨機解調方案見圖3。

根據壓縮感知的定義，基于隨機解調的模擬信息轉換器有:

y=HP(x+z)+w=A(x+z)+w

(1)

圖3 基于確定序列的隨機解調方案

其中：A=HP，H是低通濾波器響應，P是混頻序列；z是信號噪聲；w是測量噪聲。

解調過程表達為

(2)

其中F為投影矩陣。

chirp信號取代了傳統隨機解調方案中的PN序列。

2.2 多通道重構的信噪比性能分析

由于噪聲信號的混疊，在壓縮采樣信號重構過程中會引入額外的信噪比損失，這會嚴重影響雷達或通信系統的性能。利用多路結構與隨機解調壓縮采樣技術，能夠有效克服隨機解調結構引入的額外信噪比損失。

將模擬信號通過功分器進行K路壓縮采樣，其表示為:

(3)

在得到的每一路壓縮采樣數據后，通過每一路的壓縮重構算法得到:

(4)

最后，在重構端得到的合并信號表示為

(5)

在重構端的噪聲協方差矩陣為

(6)

由于AHA的對角線元素近似為1，而非對角元素是隨機分布的，因此K路積累后近似為

(7)

忽略測量噪聲的影響，公式(7)解釋了在重構端信號本身的熱噪聲是無法被抑制的，能夠抑制的噪聲是由于感知矩陣結構帶來的噪聲疊加部分；多通道模式下的噪聲方差隨著通道數K的增加而減少，如果K足夠大的話，就能接近奈奎斯特采樣條件下的噪聲方差。圖4為雙通道積累的示意圖(空心圓表示噪聲，實心圓表示信號)。

圖4 雙通道積累的示意圖

3 SAR信號多路模擬信息轉換器的平臺設計及測試結果

3.1 實驗平臺參數及設計方案

該實驗系統是針對寬帶SAR信號設計的壓縮采樣及距離維重構系統，采用4路、基于chirp混頻序列的壓縮采樣結構，對寬帶SAR信號以1/2和1/4奈奎斯特采樣率進行壓縮采樣，克服傳統隨機解調結構對噪聲的敏感性，提升壓縮感知采樣系統對信號的重構概率。雷達回波參數見表1。

表1 壓縮感知欠采樣雷達系統實驗參數

實驗平臺設計方案見圖5，分為前端模擬信號欠采樣系統和后續數字信號處理系統。利用多通道任意發生器AWG采樣寬帶雷達回波信號以及實驗平臺所需要的寬帶chirp混頻序列，多通道壓縮采樣實驗平臺包括寬帶混頻器、低通濾波器、高速采集卡及便攜式大容量存儲設備等。

主要器件性能參數:功率分配器選型為ZC4PD-153+，一分四，工作頻段6～15 GHz；寬帶混頻器選型為M1-0212LA，工作頻段2～12 GHz；濾波器選型為SPL-50+和SPL-100+，3 dB截止帶寬分別為50 MHz和100 MHz。

圖5 實驗平臺設計方案

3.2 實驗步驟

步驟1，由Matlab產生4路不同調頻率的chirp信號作為混頻信號，下載到任意混頻序列發生器，并將該信號源的觸發方式設置為外部觸發。

步驟2，由Matlab生成一組不同時延的LFM脈沖信號作為雷達回波信號，下載到混頻序列發生器并另生成一組方波信號作為觸發信號。該觸發信號作為任意混頻序列發生器的外部觸發信號，用于模擬雷達回波的采樣門。

步驟3，將回波信號與本地4組chirp信號進行混頻，將輸出的I、Q(同相、正交)信號輸入低通濾波器，對輸出結果進行復采樣。共得到4組欠采樣數據。

步驟4，由Matlab產生4組感知矩陣，分別對4路欠采樣信號進行壓縮感知的恢復，并將結果求和輸出。

3.3 實驗結果分析

采用正交匹配追蹤算法(OMP)對4路欠采樣信號進行壓縮感知恢復，對輸出結果進行相干求和后，分別在無噪聲和加噪聲情況下對回波信號做了重構恢復，如圖6所示，在無噪聲情況下5個時延不同的回波信號被準確重構出來。

圖6 壓縮感知系統欠采樣信號恢復圖

圖7給出了在輸出信噪比為13 dB時，分別以單通道、2通道、4通道在1/2 奈奎斯特采樣率情況下使用AIC結構的重構輸出，以及與奈奎斯特采樣率下的脈壓輸出性能對比。脈壓輸出結果在正確的時延位置都有峰值輸出，但是保留了噪聲。單通道1/2欠采樣重構結果由于信噪比損失了約3 dB，第3個回波信號沒有正確重構，并且虛警較多；2通道1/2欠采樣重構結果在5個回波位置都得到了正確重構，但是虛警仍然較多；4通道1/2欠采樣重構結果所有回波位置都得到了正確重構，并且虛警較少。

圖7 不同通道數時壓縮感知的重構性能對比

圖8顯示了不同通道時欠采樣的重構概率對比，奈奎斯特采樣率下的重構概率即檢測概率，單通道1/2欠采樣重構概率性能與奈奎斯特采樣率下相差了3 dB，4通道1/2欠采樣重構概率已經接近了奈奎斯特采樣率下的檢測概率。

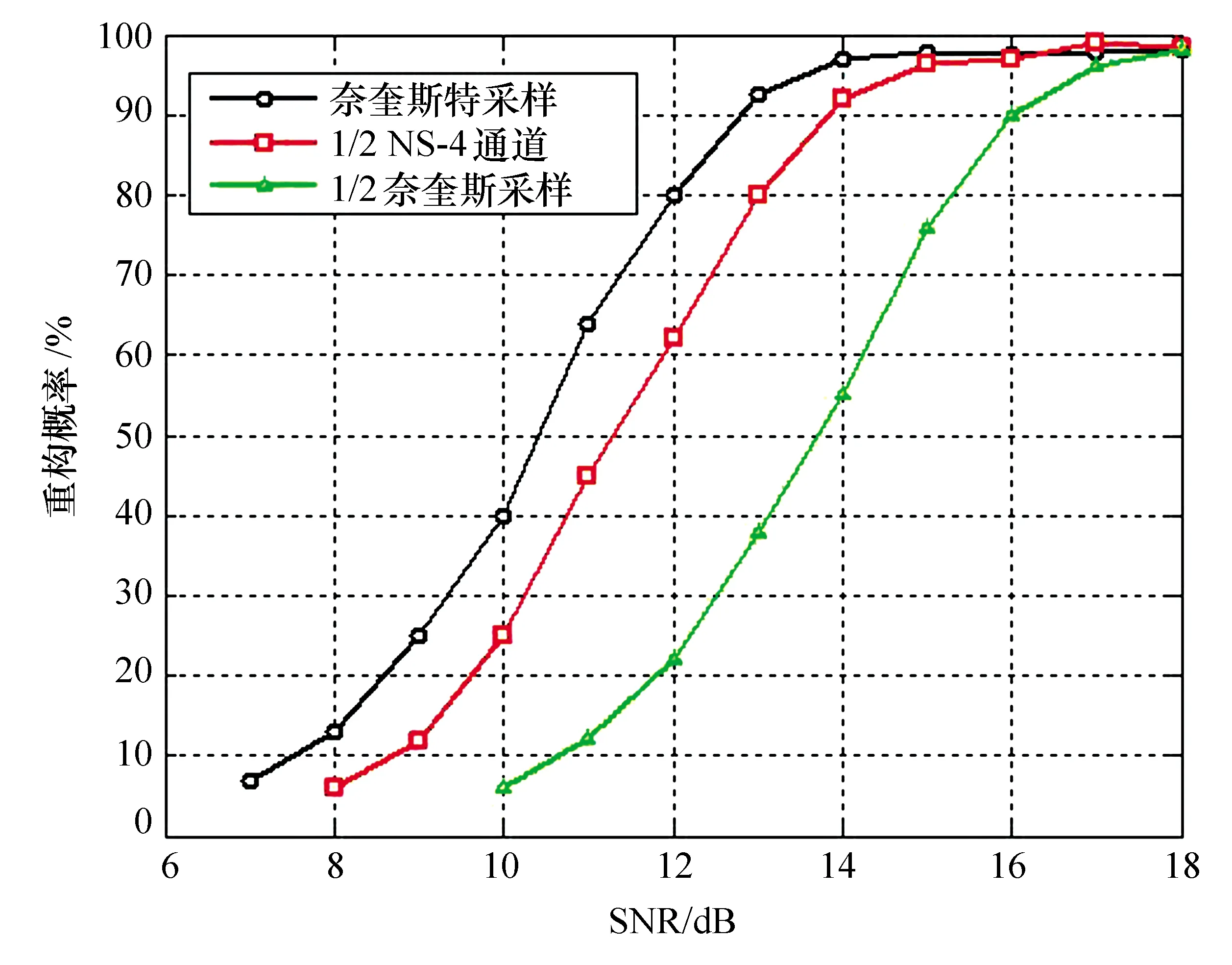
圖8 不同通道數時壓縮感知的重構概率對比

4 總結

壓縮感知技術是近年來信號處理領域的熱點研究方向，有望解決雷達、通信系統中數據量大、處理復雜等關鍵問題。本文設計的多通道AIC壓縮采樣實驗平臺有效解決了傳統AIC壓縮采樣技術存在的信噪比損失大的問題，通過采集、處理雷達回波模擬信號驗證了所提方案的合理性。該實驗平臺的設計開發對于未來亞分米級超高分辨對地觀測、超寬帶深空通信等系統的發展具有重要的理論意義和應用價值。

References)

[1] Candes E J， Romberg J， Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory， 2006， 52(2):489-509.

[2] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory， 2006， 52(4):1289-1306.

[3] Kirolos S， Laska J， Wakin M， et al. Analog-to-Information Conversion via Random Demodulation[C]//2006 IEEE Dallas/CAS Workshop on Design， Applications， Integration and Software. 2006:71-74.

[4] Laska J N， Kirolos S， Duarte M F， et al. Theory and Implementation of an Analog-to-Information Converter using Random Demodulation[C]// 2007 IEEE International Symposium on Circuits and Systems. 2007:1959-1962.

[5] Ragheb T， Laska J N， Nejati H， et al. A prototype hardware for random demodulation based compressive analog-to-digital conversion[C]// 2008 51st Midwest Symposium on Circuits and Systems. 2008:37-40.

[6] Tropp J A， Laska J N， Duarte M F， et al. Beyond Nyquist: Efficient Sampling of Sparse Bandlimited Signals[J]. IEEE Transactions on Information Theory， 2010， 56(1):520-544.

[7] Mishali M， Eldar Y C. From Theory to Practice: Sub-Nyquist Sampling of Sparse Wideband Analog Signals[J]. IEEE Journal of Selected Topics in Signal Processing， 2010， 4(2):375-391.

[8] Mishali M， Eldar Y C. Expected RIP: Conditioning of The modulated wideband converter[C]// 2009 IEEE Information Theory Workshop. 2009:343-347.

[9] Moshe M， Yonina C， Oleg D， et al. Xampling: Analog to digital at sub-Nyquist rates[J]. IET Circuits， Devices & Systems， 2011， 5(1):8-20.

[10] Shi G， Lin J， Chen X， et al. UWB echo signal detection with ultra-low rate sampling based on compressive sensing[J]. Circuits and Systems II: Express Briefs， IEEE Transactions on， 2008， 55(4):379-383.

[11] 屈樂樂，黃瓊，方廣有. 基于壓縮感知的頻率步進探地雷達成像算法[J]. 系統工程與電子技術， 2010， 32(2):295-297.

[12] 石光明， 劉丹華， 高大化， 等. 壓縮感知理論及其研究進展[J]. 電子學報， 2009， 37(5):1070-1081.