初中數學教學中培養學生發散思維能力的策略探討

蘇琴

（江蘇省常州市武進區牛塘初級中學，江蘇常州 213163）

現如今新課程改革和發展，各個學校更加注重學生的創新思維培養。數學具有較強的抽象性而且邏輯性嚴密，是培養學生發散思維最佳途徑。在初中數學教學過程中，除了要學生掌握一些基本知識，還需要引導學生在學習數學知識時運用新途徑去思考和分析，通過新方法去探究數學問題[1]。在2011年頒布的《初中數學課程標準》中指學習數學的主要目的是發展學生的思維，將傳授知識作為培養學生創新思維的一種方法。由此可以得出，數學教學對培養學生發散思維是多么重要。

1 初中數學教學現狀

初中數學課堂教學中的教師與學生間互動過于單一。一般情況下，老師普遍偏向成績較好的同學，同其他學生相比更加重視這些學生，因此在課堂教學中老師喜歡向這些同學提問。認為這些同學提出的問題更有見解，同時對其他學生的學習更有啟發，也能夠節省課堂時間，提高學生們學習效率。其實恰恰相反，這樣做在一定程度上起到積極作用，但長期下來，弊大于利，參與課堂教學的還有其他學生，老師的忽視會導致他們從最開始希望參與課堂互動，漸漸地發生了轉變，開始作為旁觀者，不愿意與老師互動，也不愿去思考問題，這樣不利于初中數學發散性思維能力的培養。

有時老師太過于注重和學生們互動，導致部分學生喪失學習的主動性。隨著新課改的不斷展開和深入，老師根據新課改要求對課堂教學有了一定的了解，也逐步實施在自己的課堂的教學過程中，加強并增多了師生之間的互動次數。但由于對新課改的本質內涵的理解有偏差，在初中數學課堂教學中的師生互動方面出現了許多問題。比如把提問數量作為課堂互動性的唯一衡量標準，導致學生的主動性被忽視，從而產生對課堂教學的厭倦疲憊感，也就難以培養對初中數學的發散性思維能力。

初中課堂教學中的師生之間頻繁互動，導致學生沒有充足的時間去思考問題，去解決方法。當把課堂教學質量的唯一標準設定為課堂教學中的師生互動次數和狀況，老師在課堂中向學生們提出一個問題后，沒有給學生充足的時間去思考和分析，立刻說出答案來，長時間下來使學生產生了依賴情況，導致對問題解決惰性思想。或是有時老師會在未解決前一個問題就拋出了下一個問題，把學生被弄得迷糊，不能集中精力進行課堂學習[2]。比如在蘇教版數學課堂上老師提問:對對稱講解時，只是講解兩者的原理和區別，然后在課堂中講解中展示模型與學生互動，讓學生列舉種種生活中對稱物體，卻忽視了足夠讓學生探索其原理，阻礙了學生自主學習能力的發展，不能促進高效課堂的發展。

2 初中數學發散性思維能力培養

初中生正處于思維發展的關鍵時期，培養學生創新思維，就需要我們通過教學、引導學生解決數學問題讓，讓學生在學習數學過程中發現樂趣。在新時期數學教學過程中，我們教師要通過對學生們提問，來引導和組織學生們去探究、去解決問題，在這個過程中我們還需要設計相關的教學步驟。例如，在向學生提出的問題，應當改變過去傳統完全依賴教材模式的問題模式，更加要注重依據教學內容大綱跟學生進行互動教學學情，并結合學生們現實生活經歷為學生們創造出相關的問題，激發他們對學習的興趣，這樣才能夠有助于培養并提高學生的思考能力。如教師在講到“圓”這一內容時，我們可以借助計算機模擬技術為學生展示圓是如何從一個方形切割成圓的視頻，在通過介紹我國古代對圓面積的計算過程，然后再計算機推算出π的計算，并結合生活觀察周圍圓的相關物體。通過這樣的形式啟發學生的思維，拉近教學知識與學生生活的聯系。然后，教師可以讓學生拿出準備好的剪刀、彩色紙等工具，通過對裁剪對圓有深度了解。通過這樣的教學形式，增加教學的趣味性，可以讓學生積極主動的參與課堂教學活動中。同時，在以上教學活動中，通過學生的親自參與與自主思考，有助于激發學生學習興趣，培養學生思維能力與創新能力。

從一題多變中培養學生思維技巧“一題多變”是一種以最基本的問題背景為模型，通過不斷改變問題的條件、背景、問題的描述方法或問題的設問方式而演變成新問題的一種訓練方式。其目的是為學生可以從多角度、多層次對問題進行思考探究，從而使學生在訓練中思維得到靈活發展。這種問題在初中數學中經常出現，因此，教師可以抓住一題多變的特點，培養學生的思維技巧。以“燃燒速度”這一知識為例，知識講解之后教師為學生設置了以下問題，比如，取出一根繩子同時點燃兩端，繩子在4分鐘燃燒完；在取出一根繩同時點燃兩端，燃盡的在點第二根繩子的一端，兩根繩子燃燒完成需要16分鐘。規則：（1）計算一個時間最多只能使用3條繩子。（2）只能在繩子的端部點燃。（3）可以同時在幾個端部點火。（4）點著的火中途不滅。（5）不許剪斷繩子，或將繩子折起。根據上面的5條規則下列時間能夠計量的有（）。 A、6分鐘；B、7分鐘；C、9分鐘 D、10分鐘；E、11分鐘；F、12分鐘”通過這樣的變式逐步增加題目的難度，不僅增加數學趣味性，還可以促進學生知識的遷移，逐漸提升學生的思維技巧。

從一題多解中培養學生發散思維 “一題多解”與“一題多變”的目的相同，是為啟發、引導學生從不同角度、不同層面、不同思路進行思考、分析、解決問題的一種訓練方式。與之不同的是，一題多解強調學生運用不同的方法解決同一個問題，是一種改變學生固化思維，調動學生思維積極性，鍛煉學生思維靈活性，引導學生掌握知識的縱橫聯系的思維方式。因此，在初中數學教學中，教師應注重借助“一題多解”來培養學生的發散性思維。如圖1，△ABC內部一點D關于邊AB,AC的對稱點分別是點E,F。(1)判斷△AEF的形狀，并說明理由；(2)說明∠EAF與∠BAC的關系，并說明理由；(3)滿足什么條件時，E，A，F三點在一條直線上？(4)滿足什么條件時，△AEF為等邊三角形？拓展學生的思維能力。

教師可以以“比賽”的形式展開教學活動，鼓勵學生運用多種方法解答以上問題，最終選出方法最多且答案都正確的四名學生，教師將給予其適當的獎勵。通過這樣的形式改變了學生固定的思維模式，可以使其積極主動地參與課堂教學中，依據題目給出的條件多角度、多層次的思考解題方案，有助于促進學生發散性思維的形成。

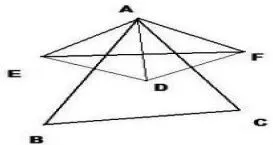
圖1 幾何圖

3 結語

總之，發散性思維是要求初中學生需要要具備的一種思維能力，我們可以通過數學教學活動，來鍛煉并提高學生們思維能力，從而激發他們對學習熱情，來達到提升學生學習效率，這樣能夠有效地提升他們的數學成績。在此，我們教師在初中數學教學過程中，時刻要重視對學生數學思維能力的培養，不能輕易放松。而且要采取多種教學方式，靈活且有效的運用新的教學方法，來培養發散性思維，有效促進學生創新能力的有效提升，我們的任務任重而道遠。

[1]丁宏玉.關于初中數學發散性思維能力培養策略分析[J].數學學習與研究，2016（18）:91.

[2]張俊忠，肖宏治.初中數學發散性思維培養策略探究[J].蘭州教育學院學報，2016（9）:163-165.