液壓泵控缸伺服系統T-S模糊模型在線辨識研究

鄭 維，王洪斌,，張志明，葛俊禮,任素波,3

(1. 燕山大學 電氣工程學院，河北 秦皇島 066004； 2.中國重型機械研究院燕山大學分院，河北 秦皇島 066004；3.燕山大學 機械工程學院，河北 秦皇島 066004)

0 前言

直驅式電液伺服系統使用交流伺服電機代替傳統的電液伺服閥，通過改變泵的轉速來改變其輸出流量，具有結構簡單、節能高效、可靠性高、性能穩定等顯著優點，廣泛應用在工業、國防、航天等領域[1-4]。目前對于泵控缸電液位置伺服系統普遍采用機理分析建模方法，因其物理參數檢測困難，而導致此建模下的系統精度低、泛化能力差，不能夠反映系統固有的非線性和時變性特性。

本文以電機直驅液壓泵控缸伺服系統的輸入輸出數據為依據，闡述泵控缸伺服系統的工作原理及其控制過程，并在研究過程中引入T-S模糊模型辨識理論，T-S模糊模型能夠以局部線性化為基礎，運用模糊推理的方法實現全局的非線性。通過分析和探討泵控缸系統的輸入量、輸出量、被控量以及需要辨識的參數之間的關系，將泵控缸伺服系統與T-S模糊模型有機的結合起來。通過分析比較總結出此智能控制的特點，為分析泵控缸電液位置伺服系統的非線性特性提供了一種可行的方法。該方法對于進行高精度的伺服控制策略的研究有著較為重要的意義。

1 T-S模糊模型

1.1 T-S模糊模型結構

T-S模型是由日本學者Takagi-Sugeno提出，它以局部線性化為基礎，是通過模糊推理實現系統全局非線性的一種辨識方法[5]。T-S模糊模型通過if-then 結構來描述非線性系統， 其中的每一條規則都代表一個線性子系統。對多輸入——單輸出的非線性系統而言，可以由c條模糊規則組成的集合表示,其中第i條模糊規則表示為

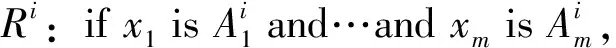
(1)

(2)

1.2 T-S伺服系統T-S模糊模型辨識

T-S模糊模型的辨識分為結構辨識和參數辨識兩部分。結構辨識是對輸入輸出變量進行模糊空間劃分，以便確定模糊模型規則數目等。參數辨識是根據某種特定準則，對模糊模型參數進行辨識調整。一般來講，應先辨識出前提變量的結構和參數，再辨識結論參數。本文采用前提變量和結論參數分開辨識的方案，采用文獻[5]提出的模糊辨識算法，利用測得的輸入輸出數據來計算泵控缸位置伺服系統非線性動態模型，同時采用(IFP-FCM)改進模糊分割聚類算法，簡化T-S模糊規則及前提變量參數的生成，同時運用加權最小二乘法得出結論參數。

2 泵控缸液壓位置伺服系統模型辨識

2.1 泵控缸液壓位置伺服系統基本結構

液壓伺服系統基本結構如圖1所示。

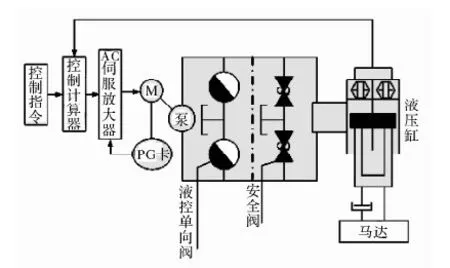
圖1 泵控缸位置伺服系統結構示意圖

該系統通過控制伺服電機輸入電壓的大小，進而改變電機轉速，同時利用電機調速來實現液壓泵輸出流量與負載所需流量相同。其中伺服電機輸入電壓是T-S模糊模型辨識的前提參數。液壓系統進行工作時，安全閥處于常閉狀態，用于過載保護；單向閥起到補油作用，用來補償因油缸面積差造成的油量不足以及泵和油缸的泄漏。其中單向閥控制端口壓力用來決定補油壓力值，定量泵回油口用來供給油泵所需的油液。輸入的位置指令與檢測的位置信號分別用來控制計算器輸出與位置偏差，從而得到對應的轉速指令信號。并將此信號同編碼器測得的電機實際轉速信號進行較，獲得轉速偏差信號。轉速偏差信號經放大器放大后用于控制伺服電機，從而驅動定量泵按要求轉速運行，最終實現對油缸和負載的精確位置控制。

2.2 泵控缸位置伺服系統T-S模糊模型

本文針對泵控缸伺服系統T-S模糊模型進行定性研究，實驗過程中為了便于辨識數據，輸入端采用隨機信號。實驗中生成兩組數據，一組為辨識數據，一組為校驗數據。其中試驗數據包括輸入和輸出數據，輸入信號及為設定值與反饋值形成的偏差值，輸出信號為采集到的液壓缸活塞位移。泵控缸位置伺服系統控制裝置如圖2所示。

圖2 泵控缸位置伺服系統控制裝置

2.3 確定隸屬函數

本文在傳統FCM算法的基礎上，提出了一種改進的模糊分割聚類算(IFP-FCM)，并將此方法應用到液壓泵控缸伺服系統，對其進行模型辨識。

首先引入隸屬度約束函數為

(3)

其次，構造新的目標函數

(4)

式中，xj為系統狀態變量；μij為模糊模型隸屬度；vi為模糊模型隸屬度中心；c為聚類數；n為模糊模型迭代次數；i和j為迭代因子；m為權重指數，又稱作平滑因子，直接影響IFP-FCM的模糊度。

IFP-FCM聚類算法的模糊度是通過調整權重指數m實現，因此必須選定合適的m值。Ludwig S A[6]給出了m的經驗取值范圍1.15≤m≤5；然后從物理層面進行解釋，得出m=2時最有意義。進而文獻[7]則從模糊聚類的有效實驗中得出m的最優選擇區間1.5≤m≤2.5，本文實驗過程中取m=2。

利用算法的收斂特性推導出關于隸屬度μij和隸屬度中心vi的迭代公式，得到T-S模糊隸屬度迭代公式，使得該方法能夠有效的對抗多頻噪聲和外界擾動，使控制系統具有更好的魯棒性。最后利用拉格朗日優化理論對目標函數(4)進行求解，當且僅當目標函數取(4)最小值時，得到vi和μij為

(5)

(6)

2.4 選取聚類自適應參數

為了保證泵控缸伺服系統T-S模糊模型的能夠有更高的辨識精度和收斂速度，針對在線計算、實時決策、過程控制、等要求較高的液壓控制領域，選擇合適的聚類自適應參數顯得尤為重要。對控制系統進行聚類分析的目標是將相似度最大的被控制量劃分到同一簇，而不同簇之間的相似度又最小。依據此類中心思想，本文給出了聚類數 的自適應函數L(c)為

(7)

(8)

從式 (7)和(8)可以看出，如若L(c)的取值越大，說明對系統的分類越合理。當L(c)取最大值時，對應的c值即為最佳值。

綜上所述，針對泵控缸液壓位置伺服系統，基于參數自適應的IFP-FCM模糊聚類方案完整描述如下：

Step1：給定迭代標準ε，聚類數c的初始值c=2，L(1)=0，定義初始分類矩陣為V(k),其中K=0。

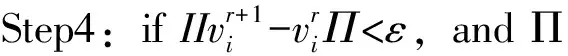
Step5：利用公式(7)計算聚類自適應函數L(c)，ifL(c)>L(c-1)，andL(c)>L(c+1)，then模糊聚類過程結束；else置c=c+1，轉向第2步。上述方案可以自動找出最佳的聚類參數c值，以及相應的聚類中心和劃分隸屬矩陣，進而可以得到模糊辨識的前件參數和結構，即系統的隸屬度函數和模糊規則。

2.5 后件參數辨識

對于液壓泵控缸伺服系統而言，其實際機械結構不會發生變化，那么在辨識過程中模型的規則數目，前提變量的選擇也不會發生變化，基于伺服系統的此類特點，本文采用帶有遺忘因子的遞推最小二乘方式對伺服系統進行在線學習，此方法可以克服最小二乘法需要對矩陣 求逆的缺陷[8,9]。給定輸入輸出數據，則系統的輸出量表示為

Y=XP

(9)

其中，

Y=[y1,…,yn]T

(10)

(11)

其中，λ為遺忘因子，若λ值越小，則表示該伺服系統對新的數據的學習能力越強。 本文選取遺忘因子λ=0.85。初始條件設置為：P0=0，S0=αI，其中α≥10 000，本文取α=10 000。I為L×L的單位矩陣。為避免對某種工況的過度學習而造成模型泛化能力下降，本文采用選擇性在線學習，即每次進行學習時，首先計算每條規則對應的激勵強度，然后只針對最大激勵強度的模糊參數規則進行學習，其它規則的參數則保持不變。

3 仿真分析

首先由于泵控缸伺服系統的固有頻率比較低，所以本文中選取模糊程度常數η為0.10，聚類算法的模糊度權重指數選取m=2，其次由于泵控缸位置伺服系統的控制輸入電壓選取范圍為-5～5 V，因此本文仿真實驗中偽隨機多幅值信號的幅值范圍為-5～5 V之間。將經過功率放大器放大后的偽隨機多幅值信號作為泵控缸伺服系統的仿真實驗中的輸入信號，并且利用檢測裝置實時測量液壓缸的活塞位移xp便可得到系統輸入/輸出數據，即辨識過程中的輸入輸出曲線，如圖3、4所示。文中選取1000組輸入/輸出數據對，輸入變量為控制電壓U，輸出變量為液壓缸活塞位移xp。

圖3 控制電壓辨識數據

圖4 輸出位移辨識數據

利用系統的輸入輸出量，即可根據前面提到的參數自適應IFP-FCM模糊聚類算法的步驟進行模糊辨識，模糊辨識步驟如下：

Step1：設定初始參數，迭代標準 ，初始聚類c=2，L(1)=0，初始分類矩陣V(k),K=0；P0=0,S0=αI，α=100 00，IL×L是單位矩陣；

Step2：根據參數自適應IFP-FCM模糊聚類算法對辨識樣本數據輸入變量進行聚類，并計算出前提參數μij和vj；

Step3：根據式(6)生成矩陣X和Y；

Step4：利用帶有遺忘因子的遞推最小二乘法辨識出后件參數P。

通過理論分析，可以把U(k)、U(k-1)、U(k-2)和xp(k-1)、xp(k-2)、xp(k-3)作為模糊模型輸入量，xp(k)為輸出量。選取圖3和4中前1 000組數據作為訓練數據，后200組數據作為檢驗數據，在MATLAB環境下進行編程實現。其中訓練的均方誤差MSE=0.0128，CPU運行時間T=0.2000；檢驗的MSE=0.0185，CPU運行時間T=0.1850，辨識結果如圖5、圖6所示。MSE代表估計值與真值之差平方的期望值，MSE的值越小，表明辨識模型精確度越高，越接近實際系統。由MSE和CPU的運行時間數據可知，經過T-S模糊辨識得到的泵控缸位置伺服系統的辨識精度高，泛化能力強，泵控缸伺服系統的固有非線性特性也在此過程中進行了較好的擬合。

圖5 訓練數據辨識結果

圖6 檢驗數據辨識結果

4 結論

本文以電機融合泵直驅泵控缸伺服系統為研究對象，利用了T-S模糊辨識方法對其進行動態辨識，辨識出液壓缸活塞位移的輸出變化模型。首先采用參數自適應IFP-FCM模糊聚類算法對伺服系統的輸入空間進行劃分，其次利用帶有遺忘因子的遞推最小二乘法辨識結論參數。由此得到泵控缸位置伺服系統的T-S模糊模型的前后件參數。仿真實驗結果表明基于T-S模糊模型的伺服系統在線辨識具有結構簡單、辨識精度高、自適應性強、辨識過程CPU運行時間短等特點。

[1] 劉寶權, 王軍權, 張巖,等. 帶鋼冷連軋液壓與伺服控制 [M]. 科學出版社, 2016.

[2] 喜冠南, 彭根運, 顏國義, 等. 電控比例液壓泵控通用液壓機開環實驗研究 [J]. 液壓與氣動, 2011, (07): 65-67.

[3] 景健, 權龍, 黃家海, 等. 非對稱泵直驅液壓挖掘機斗桿特性研究 [J]. 機械工程學報, 2016, (06): 188-196.

[4] 李金龍,孔祥坤,張業燾. 一種比例泵在RH精煉爐液壓系統中的應用 [J]. 重型機械, 2011, (03): 8-10.

[5] Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control [J]. Readings in Fuzzy Sets for Intelligent Systems, 1985, 15 (01): 387-403.

[6] Ludwig S A. MapReduce-based fuzzy c-means clustering algorithm: implementation and scalability [J]. International Journal of Machine Learning and Cybernetics, 2015, 6 (06):1-12.

[7] Bora D J，Gupta A K. A Comparative study Between Fuzzy Clustering Algorithm and Hard Clustering Algorithm [J]. International Journal of Computer Trends & Technology, 2014, 10 (02): 108-113.

[8] 張虎, 李正熙, 童朝南. 基于遞推最小二乘算法的感應電動機參數離線辨識 [J]. 中國電機工程學報 2011, 31 (18): 79-86.

[9] 宋繼捷. 輸出誤差模型基于數據濾波的遞推最小二乘辨識 [D]. 哈爾濱工業大學, 2013.