證明一個曲面方程表示柱面的兩種有效途徑

鄧翠容

在《空間解析幾何》中，柱面是一種常見且重要的曲面.關于柱面方程的求解分析及幾何圖形教材中都給了規范的做法.但是反過來，給出一個三元曲面方程，我們要證明它表示一個柱面，這個問題就復雜了，很多學生不會解答這一類題.對此，本文將介紹證明方程表示一個柱面的兩種方法，以期幫助大家掌握這個問題.

1 基本定義

由平行于某一定方向且與一條空間定曲線相交的一族平行直線所組成的曲面叫做柱面.定曲線叫做柱面的準線，平行直線族中的每一條都叫做柱面的（直）母線，定方向是直母線的方向，也叫做柱面方向.

2 證明方程表示的曲面為柱面

思路一 構造空間中的一族平行直線，使得它們能夠生成這個曲面，這樣就證明了該曲面是一個柱面.

思路二 我們將作出一個柱面，它的準線可取為坐標面與題中所給曲面的交線，母線方向設為v→=（X，Y，Z），然后求出這個柱面的方程，再將這個柱面方程與題中所給的方程比較，以確定v→=（X，Y，Z）使兩方程一致，這樣就證明了題中所給的方程表示的曲面是一個柱面.

下面我們通過兩個例題來分別說明這兩種方法的應用.

例1 證明方程

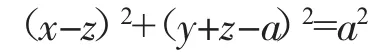
表示一個柱面.

證明 將方程（x-z）2+（y+z-a）2=a2改寫為

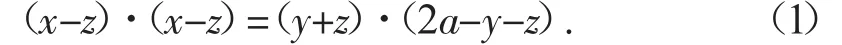
將原方程即（1）式表示的曲面叫做S.

作方程組

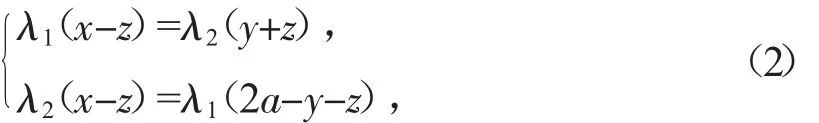
其中 λ1，λ2是不全為零的任意實數.對于 λ1∶λ2的每一個值，方程組（2）表示一條直線，因此方程組（2）表示一族直線，稱為λ族直線，下面證明λ族直線可以構成整個曲面S，從而該曲面為柱面.為此，需要證明下面兩點：

（1）λ族直線中的每一條直線都在曲面S上.

當 λ1λ2≠0 時，將（2）式中的兩式相乘得到（1），可見直線（2）在曲面 S 上.當 λ1λ2=0 時，不妨設 λ1=0，λ2≠0，此時（2）變為

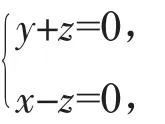
顯然這條直線也在曲面S上.同理可證得當λ1≠0，λ2=0時相應的直線也在曲面S上.

（2）在曲面S上的每一點處，必有λ族直線中的一條直線經過該點.

設P0（x0，y0，z0）是曲面S上的任意一點，則有

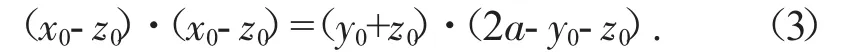
作方程組

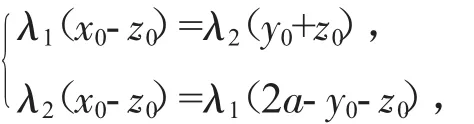
這是一個關于λ1，λ2的二元一次齊次方程組，由（3）式知系數行列式等于零，從而上述方程組有非零解，因此可以唯一確定比值λ1∶λ2，于是在λ族直線中有唯一的一條直線經過P0點.

綜上可知，曲面S為柱面.

例2 證明方程

2x2+5y2+2z2-2xy-4xz+2yz+2x-10y-2z-1=0表示一個柱面.

分析 這是一個三元二次方程，而且各項都齊全，如果想把它像例1那樣，把它改寫為一次因子的乘積，再由此寫出生成曲面的直線族是比較困難的，為此我們用上面的思路二來解答.

證明 取曲線

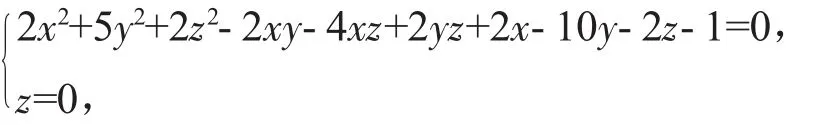
即

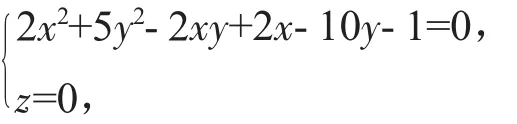
為準線，母線方向為v→=（X，Y，Z）來建立柱面的方程.

設 P（x，y，z）是柱面上任意一點，則點 P 必定落在某條母線上，即存在準線上一點P1（x1，y1，z1），使得點 P 位于過點 P1且以v→=（X，Y，Z）為方向向量的直線上，于是有

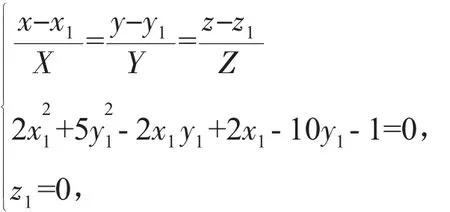
由方程組消去 x1，y1，z1得

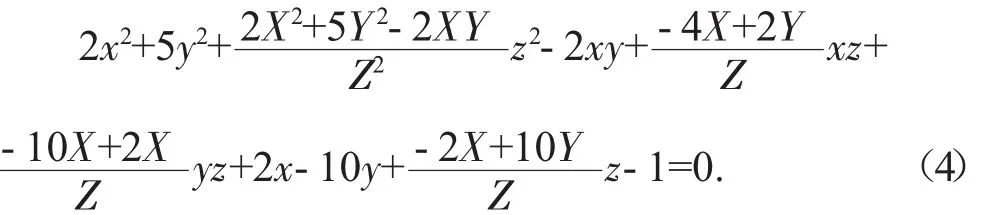
將此式與原方程比較，并取

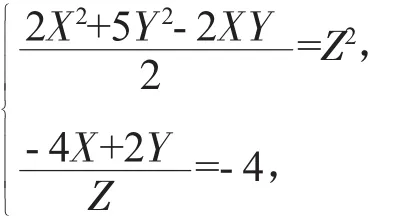
由此方程得 X∶Y∶Z=1∶0∶1，帶入（4）得到的方程即為原方程

2x2+5y2+2z2-2xy-4xz+2yz+2x-10y-2z-1=0，所以原方程表示的曲面是一個以

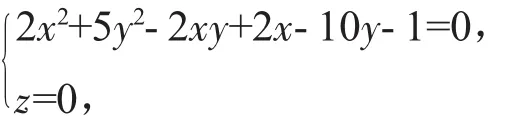
為準線，母線方向v→=（1，0，1）的柱面.

評注 當方程容易改寫為一次因子的乘積時，用例1的方法，計算簡單些.當方程不容易改寫為一次因子的乘積時，用例2的方法.對于證明方程是柱面的問題，例2的方法是普遍適用的，只是計算量比較大.

[1]李養成.空間解析幾何（新版）[M].北京：科學出版社，2008：74-76.

[2]丘維聲.解析幾何（第二版）[M].北京：北京大學出版社，2007：83-84.