具有狀態合法性驗證的區塊鏈一致性算法研究
, ,,
(1.中國科學院計算機網絡信息中心,北京 100190; 2.中國互聯網絡信息中心,北京 100190; 3.中國科學院大學,北京 100190)
0 概述
區塊鏈在不可靠的分布式環境中維護了一個公共的總賬[1],這個總賬由一系列的匿名參與者來維護和擴展。近年來,區塊鏈網絡吸引了越來越多的工程人員、學者和投資者的注意。伴隨著大量的資本投入[2],區塊鏈得到了快速部署,已經成為了一項公共基礎設施。
由于區塊鏈沒有可信任的中心節點,這使得設計和實現去中心化的域名系統(Domain Name System,DNS)[3]、公鑰基礎設施(Public Key Infrastructure,PKI)和去中心化的文件存儲成為現實。
現有金融體系中,為了確保安全,當涉及大額交易和可疑交易時通常需要特殊的監管和審查[4]。而對于去中心化的比特幣來說,不受監管是其能夠流行的部分原因之一,但同時也會給大額交易的交易方帶來潛在的風險。研究者提出讓國際貨幣基金組織(International Monetary Fund,IMF)參與到比特幣的運營中[5],但如何保證監管者IMF不成為新的中心,還尚未解決。
對于去中心化的域名系統,當域名注冊存在沖突,即權威機構和個人同時申請一個權威域名,權威域名的歸屬問題是由獲得區塊寫入機會的單個節點決定,單個節點一旦出錯,將導致此權威域名被個人注冊而無法更改。
去中心化的文件存儲系統中,有版權問題或者不合法規的資源一旦上傳成功,除了上傳者本身,其他人很難刪除。對于廣泛運行的點對點(Peer to peer,P2P)網絡而言[6],通常是在其部署爬蟲網絡來檢測非法資源的路徑,并將其加入黑名單,從而達到保護網絡的目的。爬蟲軟件只能檢測哪些資源是非法,而無法阻止資源的上傳,并且引入第三方的檢測方法,會帶來更多的問題。
上述基于區塊鏈的3種應用,都需要在不安全的分布式環境中保持全局一致性。轉賬交易的記錄、域名的管理、文件的上傳和更改,對外都需要保持一致性。每一個具體的操作,都涉及了狀態的轉換。上述問題的根源在于,區塊鏈在寫入時,只需要提供正確工作量的證明,而不對其狀態轉換進行合法性驗證。
不安全的分布式環境中的一致性問題稱為拜占庭一致性[7]。最初拜占庭一致性問題需要指數級的算法才能解決,隨后人們提出了多項式級別的拜占庭協議[8],極大降低了拜占庭系統的開銷,使其在分布式系統中的應用成為可能。解決拜占庭一致性的算法大致可分為2類:中心化算法和去中心化的算法。
去中心化算法能夠解決中心化算法中存在的單點故障,并且能夠容忍更多的故障節點。區塊鏈技術作為去中心化算法的代表,其有效性經歷了廣泛的實踐驗證。但去中心化一致性算法存在未考慮到狀態轉換的合法性由誰決定的問題。區塊鏈的處理方法是由獲得區塊寫入權力的單個節點決定,這就違背了去中心化的初衷。因此,本文在區塊鏈協議上引入了合法性驗證的法定人數投票,由法定人數對系統的狀態轉換有效性進行驗證。
1 相關研究
拜占庭將軍問題是點對點通信中的基本問題,其含義是一些拜占庭將軍率領他們的部隊要攻占敵人的一個城池,每個將軍只能控制自己的部隊,并且通過信使傳遞消息給其他將軍,將軍之中存在叛徒,如何設計一種策略使忠誠的將軍達成一個不算壞的行動協議而不受叛徒的挑撥。
隨后研究者提出了中心化的拜占庭一致性協議[9],協調者的引入降低了消息傳遞的復雜度,同時提高了最好情況下的性能。中心化算法在最好情況下,需要α輪消息交換(α是常數),但在最壞情況下,則需要α(t+1)輪消息交換[10](t是最大出錯節點個數)。中心化一致性協議中協調者的更換通常由超時條件觸發,因此,協調者能夠在不被檢測到的情況下,故意推遲消息的發送,降低系統的吞吐[11]。這促使了去中心化一致性算法的發展。因此,本文研究的重點在于如何使去中心化的區塊鏈一致性算法具有狀態合法性驗證,并提高系統容錯率。
1.1 單節點合法性驗證
兩階段提交協議[12]是在計算機網絡、數據庫領域內,為了在進行事務處理過程中能夠保持原子性和一致性而設計的一種算法。兩階段提交將一個事務的提交處理過程分成了投票和執行2個階段,協調者向所有的參與者廣播投票請求,當協調者收到了所有參與者的同意消息后,協調者廣播提交請求,當協調者收到了所有參與者的提交完成消息后,這個事務才算是提交成功。兩階段提交的優點在于消息傳遞次數少,實現方便。其缺點是容錯率低,只要有一個參與者拒絕投票或者提交失敗,整個事務無法完成。此外,兩階段協議要應用在拜占庭環境中,還需要解決選舉協調者和更換協調者的問題。
本文在兩階段提交基礎上,設計了選舉和更換協調者的策略,使其能夠在區塊鏈中完成法定人數的投票確認。當正常節點獲得區塊寫入機會進行統計投票時,執行了類似的兩階段提交協議,區別在于傳統兩階段的法定集合是所有節點,而本文的法定集合是半數節點,這提高了系統的容錯率。
1.2 多節點合法性驗證
文獻[13]提出了實用拜占庭容錯協議(Practical Byzantine Fault Tolerance,PBFT),使得拜占庭協議在分布式系統中應用成為可能。PBFT采用了主從模式(Primary and backups)和法定人數(Quorum),法定人數為2f+1,其中,f為出錯節點個數,總結點個數為3f+1。正常情況下PBFT協議的運行如圖1所示。當主節點收到客戶的請求后,向其他的從屬節點發送PRE-PREPARE消息,當從屬節點收到PRE-PREPARE消息后,如果其同意,那么向網絡中的其他從屬節點廣播PREPARE消息,并收集來自其他節點的PREPARE消息,如果收到的PREPARE消息數目超過2f,那么這個節點進入了準備就緒的狀態,然后發送再次向其他節點廣播COMMIT消息,并收集來自其他節點的COMMIT消息,如果COMMIT消息的數目超過2f,那么這個節點進入了提交狀態,開始執行客戶發起的請求,操作完成后,向客戶回復REPLY消息。
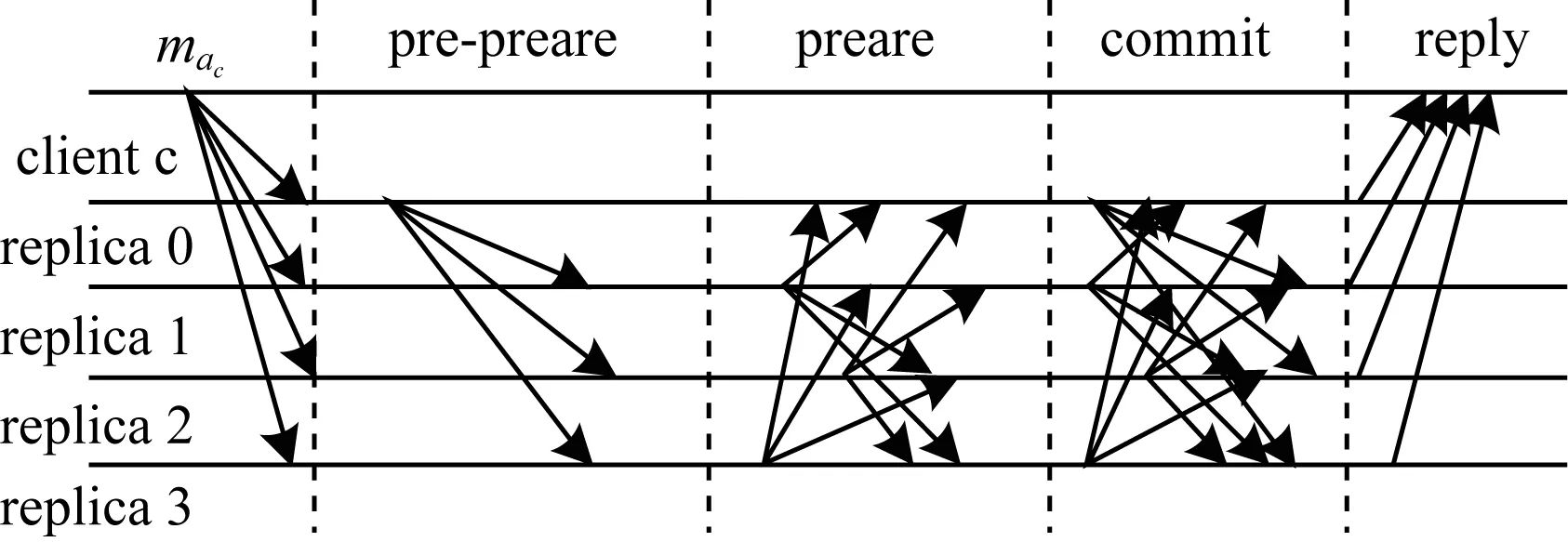
圖1 正常情況下實用拜占庭容錯協議運行情況
可以看到PBFT協議最多只能容忍總結點數的1/3的出錯節點,并且在一次同步過程中需要兩輪兩兩交互,才能使得非出錯節點達到一致,數據處理量較大。
文獻[14]提出了混合法定人數(Hybrid Quorum,HQ)來改進PBFT,其運行情況如圖2所示。HQ將寫入過程分成了2個階段,首先客戶端發起請求的同時收集服務器的狀態信息,如果有2f+1個節點處于相同狀態,并且同意執行請求,則客戶端第2次發起請求,服務器開始執行請求;否則,執行PBFT協議,由主節點重新安排請求序號。
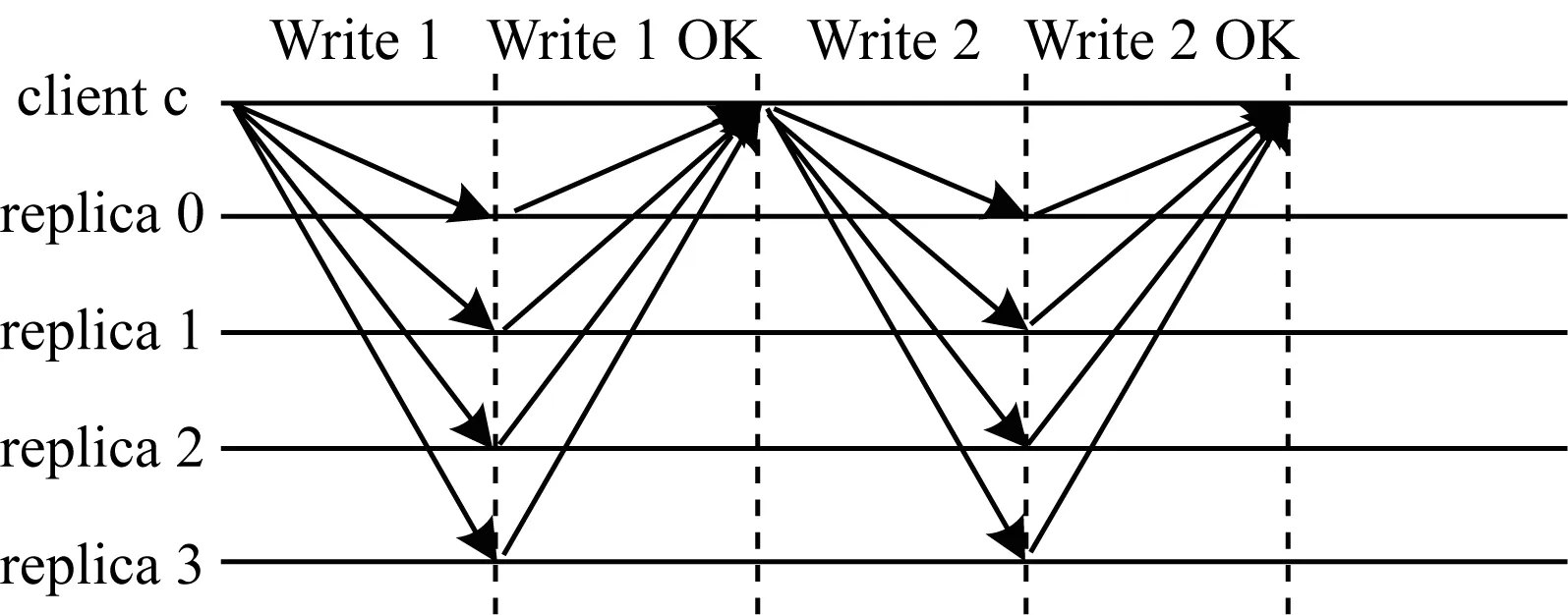
圖2 混合法定人數協議運行情況
HQ協議并沒有從根本上改變PBFT的結構,由于其對客戶端發送請求沒有競爭,服務器正常運行的情況進行了優化,使得其性能得到了提升。
PBFT協議需要兩輪的兩兩交互信息,才能容忍1/3的出錯節點,在保證狀態轉換有效的前提下,如何快速將分布式系統從一個一致性狀態同步到另一個一致性狀態,是本文待解決的問題。本文提出與PBFT不同的法定人數(Quorum),即數目為n/2+1,n為系統中節點個數,在只需要一輪兩兩交互的情況下,容忍38%的出錯節點。
2 系統模型
一個蒙特卡洛一致性協議[15]需要滿足如下3個條件:
1)可終結性,所有的過程需要在一個有限時間內做出決定。
2)一致性,所有的過程最終能夠達到一致性。
3)輸入的有效性,最終決定的值一定是過程產生的值。
2.1 消息傳遞過程
整個網絡被看做n個獨立配置的過程(process),{p1,p2,…,pn}。一個執行過程可以看做是一系列的狀態和轉換,π0,s0,π1,s1,…,πi,si,…,從狀態到可行的轉換之間由以下規則決定:
每一個轉換由一個單調遞增的時間戳,一個時間戳稱為一輪(round)。每一個過程在每一輪中只能執行一次compute指令。
匿名的過程之間通過broadcast(m)指令來傳遞消息。每條消息的最大延遲為Δ,如果消息在時間r廣播,那么每一個過程在不超過r+Δ的時間里執行receive(m)指令。
2.2 合法狀態轉換
計算模型引入了狀態合法性驗證后,原有的規則發生了變化。
2.2.1 狀態轉換
一個狀態轉換需要經過兩階段,從s0轉換到s1需要經過中間狀態π0,當一個節點發布了一個狀態轉換的消息后,收到這個消息的節點開始對這個轉換廣播自己的投票結果,同時節點開始收集消息,如果存在一個法定人數(Quorum)集合,里面所有的節點都同意,則網絡能夠被轉換到狀態s1。
2.2.2 不確定性

2.2.3 拜占庭錯誤
有f個出錯的過程,這些拜占庭錯誤節點能夠共謀對其他的正常節點發送錯誤消息。拜占庭出錯過程反對正常過程,正常過程可能會贊成拜占庭過程。正常過程提出的方案通過的概率為:
拜占庭錯誤過程提出的方案能通過的概率為:
2.3 具有狀態合法性驗證的區塊鏈算法
每一個過程在每一輪中執行一次compute過程,oracle過程將任意的輸入映射到0~1的區間,verify過程驗證事先給定的CRS,挖礦節點提供的信息nonce,區塊的哈希值Prefer三者組合是否滿足規則。一致性算法如下所示。
procedure oracle(x)
return H(x)
precedure verify(nonce,Prefer)
hash = oracle(CRS || Prefer || nonce)
Initially do
Votes = {}
Prefer = proposed_i
on receive(Votes’,Prefer’) do
If verify(v,Prefer’) and on receive_op(u,op)for all v in Votes’,all u in v and |Votes’| > |Votes| then
Votes = Votes’
Prefer = Prefer’
S = Prefer’ - Prefer
for u in S
broadcast(u,op),op = {0,1}
on receive_op(u,op)
If count(op) >= n/2
return True
else return False
on compute(r) do
nonce = coinflip
for u in Prefer
If on receive_op(u,op)
set u.status = 1
if verify(nonce,Prefer)then
broadcast(Votes || nonce,Prefer)
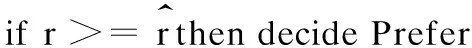
算法過程如下:
每一個節點Pi同時執行on receive、on receive_op和compute過程。
on receive過程當收到新的區塊時,執行verify過程驗證每一個區塊是否滿足工作量,對于區塊中的每一個待完成的狀態轉換,執行on receive過程,驗證其是否滿足合法性驗證。如果上述條件均滿足,并且區塊長度大于本地長度,則將這個區塊作為新的區塊。
對于新增區塊中與原有區塊鏈的差集中的中間狀態,對其狀態轉換進行投票廣播。
on receive_op過程對收到的投票進行統計,如果超過半數,就返回成功,否則返回失敗。
on compute過程執行挖礦過程,首先調用coinflip過程得到nonce,對于收到的待完成狀態轉換請求,調用on receive_op過程,修改其狀態。隨后調用verify過程,如果滿足了正確的工作量證明,則廣播這個區塊。
2.4 一致性證明
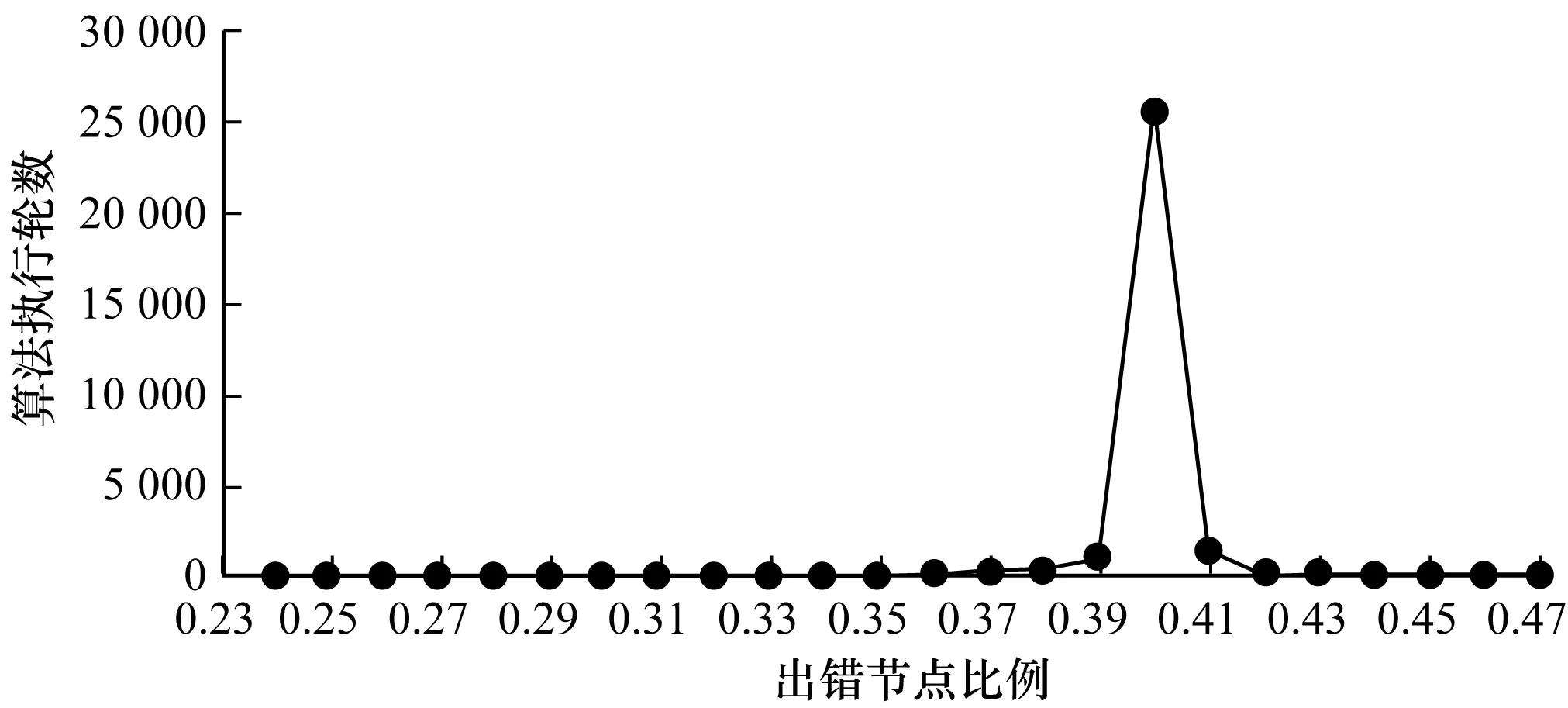
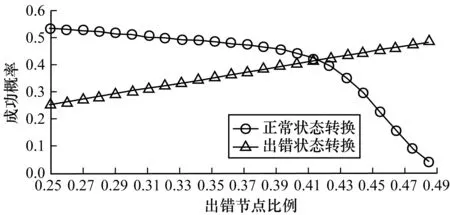
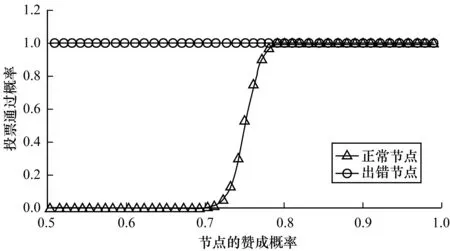
在n個process中有f 當np>5,n(1-p)>5,使用N(np,np(1-p))擬合Binom(n,p)得到: 區塊鏈協議中每個過程只會選擇最長的鏈,協議需要保證Blockc-Blockf>0,由正態分布性質得到: 而對于標準正態分布有如下性質: prob=P{u-kσ 當k=3時,prob=99.73%,當k=4時,prob=99.99%。 假設正確節點和出錯節點的提案有很大概率通過,令p≈1/n,根據公式: 圖3 執行輪數隨出錯節點比例變化曲線 算法需要保證正常節點的轉換率大于出錯節點的轉換率,這是系統正確達成最終一致性的必要條件。pc和pf隨出錯節點比例f變化曲線如圖4所示,可以看出,要使得pc>pf,則f<0.41n。 圖4 正確和出錯狀態轉換概率隨出錯節點比例變化曲線 圖5 執行輪數隨出錯節點比例f(f<0.38n)變化曲線 根據之前的實驗,選取f=0.38n作為合理的出錯節點個數。根據之前的公式: 將p′作為自變量,繪制u和v隨其變化的曲線,如圖6所示。當p′>0.75的時候,u和v差不多都趨近于1。所以,當節點對于一個狀態轉換通過的概率至少為0.75時,上述算法才能夠有效運行。 圖6 正常和出錯節點投票通過概率隨贊成概率變化曲線 本文分析具有狀態合法性驗證的拜占庭一致性協議的研究現狀,介紹多節點合法性驗證的一致性協議。針對其存在的總節點數1/3的容錯上限和2次兩兩信息交換的問題,本文提出一種具有狀態合法性驗證的區塊鏈一致性算法,設計新的法定人數集合,改進現有的區塊鏈協議。實驗結果表明,該算法使得區塊鏈一致性算法能夠具備合法性驗證,并能解決拜占庭一致性,只使用了一次兩兩信息交換,使容錯上限達到38%。 本文在網絡規模、工作量難度和通信延遲給定的假設下,使用概率模型證明了算法的正確性。下一步工作將研究如何避免這些較強的假設條件,以提高算法的健壯性。 [1] 袁 勇,王飛躍.區塊鏈技術發展現狀與展望[J].自動化學報,2016,42(4):481-494. [2] DWYER G P.The Economics of Bitcoin and Similar Private Digital Currencies[J].Journal of Financial Stability,2015,17(1):81-91. [3] ALI M,NELSON J,SHEA R.Blockstack:A Global Naming and Storage System Secured by Blockchains[C]//Proceedings of USENIX Annual Technical Conference.[S.l.]:USENIX Association,2016. [4] 楊勝剛,何 靖.反洗錢領域大額與可疑信息報告制度的經濟學分析[J].金融研究,2004,10(1):113-119. [5] PLASSARAS N A.Regulating Digital Currencies:Bringing Bitcoin Within the Reach of IMF[J].Chicago Journal of International Law,2013,14(1):377-407. [6] 陳 晗,施 勇,薛 質.P2P 網絡資源傳播模型分析及監測[J].信息安全與通信保密,2011,9(5):56-58. [7] LAMPORT L,SHOSTAK R,PEASE M.The Byzantine Generals Problem[J].ACM Transactions on Programming Languages and Systems,1982,4(3):382-401. [8] CLEMENT A,KAPRITSOS M,LEE S.Upright Cluster Services[C]//Proceedings of the 22nd ACM SIGOPS Symposium on Operating Systems Principles.New York:ACM Press,2009:277-290. [9] LAMPORT L.The Part-time Parliament[J].ACM Transactions on Computer Systems,1998,16(2):133-169. [10] BORRAN F,HUTLE M,SCHIPER A.Timing Analysis of Leader-based and Decentralized Byzantine Consensus Algorithms[J].Journal of the Brazilian Computer Society,2012,18(1):29-42. [11] 范 捷,易樂天,舒繼武.拜占庭系統技術研究綜述[J].軟件學報,2013,24(6):1346-1360. [12] LAMPORT L.Time,Clocks,and the Ordering of Events in a Distributed System[J].Communications of the ACM,1978,21(7):558-565. [13] CASTRO M,LISKOV B.Practical Byzantine Fault Tolerance and Proactive Recovery[J].ACM Transactions on Computer Systems,2002,20(4):398-461. [14] COWLING J,MYERS D,LISKOV B.HQ Replication:A Hybrid Quorum Protocol for Byzantine Fault Tolerance[C]//Proceedings of the 7th Symposium on Operating Systems Design and Implementation.[S.l.]:USENIX Association,2006:177-190. [15] ATTIYA H.Lower Bounds for Randomized Consensus Under a Weak Adversary[J].SIAM Journal on Computing,2010,39(8):3995-3904.
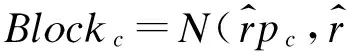
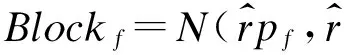
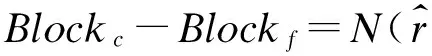
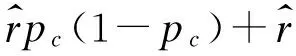

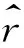
3 實驗結果與分析

3.1 出錯節點比例上限
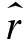
3.2 贊成概率的選擇
4 結束語

