離心風機葉片優化設計及氣動分析

曹 輝，吳廉巍

離心風機主要由葉輪、進風口及蝸殼等部件組成。葉輪轉動時，葉片構成的流道內的空氣受離心力的作用向外部運動，在葉輪中央產生真空度，因而從進風口軸向方向吸入空氣，吸入的空氣在葉輪入口處轉折一定角度后，進入葉道，在葉片作用下獲得動能和壓能，從葉道甩出的氣流進入蝸殼，經過集中導流后從出風口排出[1]。在多級離心風機中，常常使氣體進入下一級葉輪，再次提高其壓力和速度，因此其屬于流體機械的一種。流體機械廣泛應用于工業生產中的各個方面，特別是在石油化工、能源動力、航天航空等行業，在國防和經濟上發揮著巨大的作用[2]。根據目前風機的發展水平，研究和設計出更加高效節能，安全穩定，工況范圍廣的風機應該是從事該專業人員堅持不懈追求的目標[3-5]。

本文的研究對象為自主建模的離心風機，對離心風機的葉片進行幾何形狀的修改，通過CFD數值模擬的方法對離心風機整機進行氣動分析和尋找出總壓和效率有所提高的葉型。

1 數值模擬方法

在數值模擬計算中，采用商用軟件ANASYS FLUENT，利用分離式求解器和有限體積法對控制方程進行求解。壓氣機通道中的流動為湍流，采用帶有標準壁面函數的k-ε模型。利用SIMPLE算法，同時通過控制各變量的收斂精度為10-4，以滿足計算要求[6-8]。

1.1 控制方程

單位時間內流體微元體中質量的增加，等于同一時間間隔內流入該微元體的質量與流出該微元的質量的差，此定律即被稱作質量守恒定律。任何流體的流動必須遵從質量守恒定律。本文假定空氣為理想可壓縮氣體，得出質量守恒方程如下：

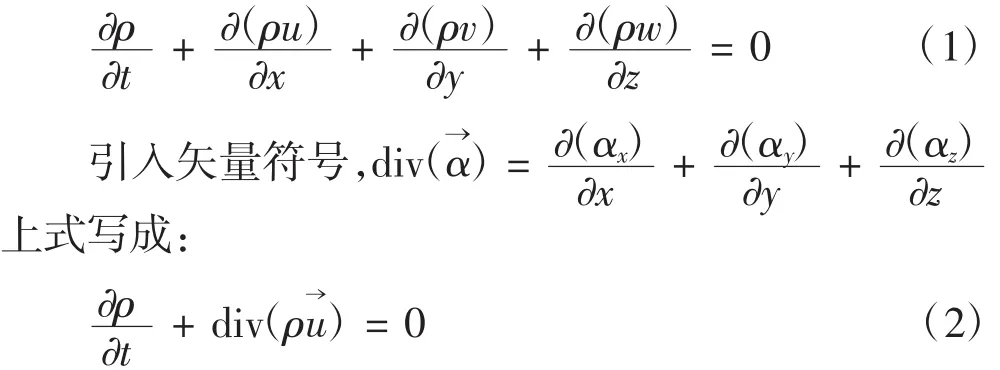
式中：ρ為流體密度（kg/m3）；t為流體流動時間（s）；u→為速度矢量；u、v、w 為速度矢量u→在 x，y 和 z方向的分量。方程（2）也可作為可壓縮氣體的連續方程。

微元體中流體的動量對時間的變化率等于外界作用在該微元體上的各種力之和，這就是動量守恒定律。任何流體的流動也同樣要遵從動量守恒定律。按照這一定律，可得到動量守恒方程：

其中，I={δij}為單位張量；Г ={τij}為粘性應力張量，對于牛頓流體有：

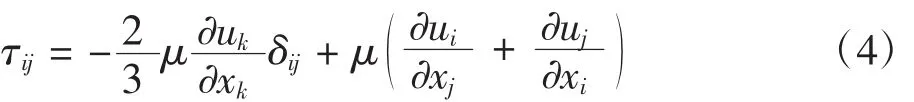
因為離心風機內部氣體流動包含一部分熱交換過程，所以還必須遵從能量守恒定律[10-13]。能量守恒定律表述為：微元體中能量的變化量為微元體內流進與流出的熱流量差，加上體力與面力對微元體所做的功。以溫度T為變量的能量守恒方程表達式為：

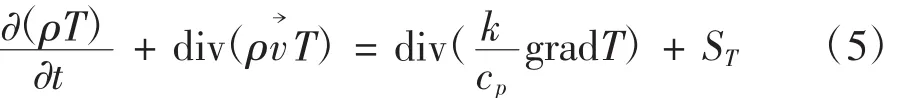
式中：Cp為流體的定壓比熱容（J/kg·K）；T為流體的溫度（K）；k為流體的導熱系數（w/m·K）；ST為流體內部熱源，有時也稱其為粘性耗散項。

綜合各個基本方程（2）、（3）、（5），發現有 u、v、w、p、T和 ρ六個未知量，還要補充一個聯系P和ρ的狀態方程，方程組才能封閉。對于理想氣體有：

式中：R為摩爾氣體常數，其值為8.314 J/mol·K.

1.2 湍流模型

本文采用的湍流模型采用標準的k-ε湍流模型。標準k-ε模型是由Lauder和Spalding提出的經典的兩方程模型，雙方程模型將湍流粘性和湍流動能相結合起來，建立其與渦粘性的關系，這種方程在工程上被廣泛采用。k-ε模型是目前應用最廣泛的兩方程紊流模型。大量的工程應用實踐表明，該模型可以計算比較復雜的紊流，比如它可以較好地預測無浮力的平面射流，平壁邊界層流動，管流，通道流動，噴管內的流動，以及二維和三級無旋和弱旋加流流動等。k-ε模型假設湍流粘性和湍動能及耗散率有關，標準k-ε湍流模型的輸運方程為：

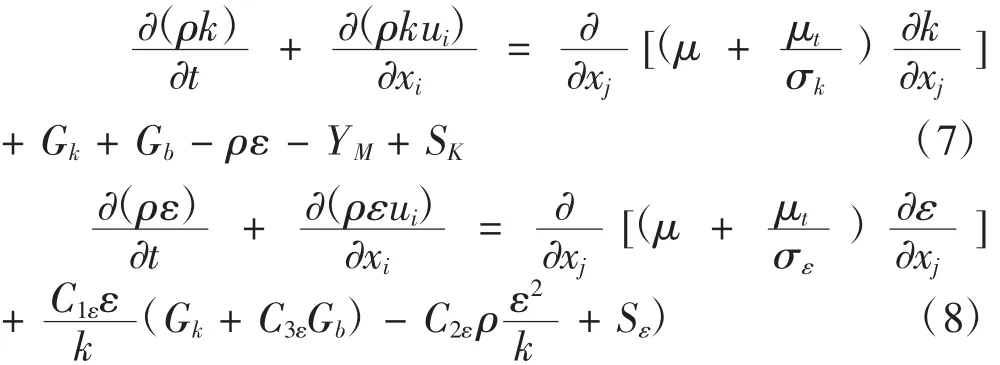
其中，Gk是由于平均速度梯度引起的湍動能k的產生項，Gb是由于浮力引起的湍動能k的產生項，YM代表可壓湍流中脈動擴張的貢獻，C1ε、C2ε和 C3ε為經驗常數，σk和σε分別是與湍動能k和耗散率ε對應的Prandtl數，Sk和 Sε是用戶定義的源項[7]。根據Launder等的推薦值及后來的實驗驗證，模型常數C1ε、C2ε、Cμ、σk、σε的取值為：

C1ε=1.44，C2ε=1.92，Cμ=0.09，σk=1.0，σε=1.3

2 前處理

2.1 計算模型建立及網格劃分

本文主要對離心風機的葉片進行分析和計算，主要討論不同葉片幾何形狀對離心風機整體性能的影響，所以忽略傳動軸，集流器等部件[9-12]。采用CFturbo對離心風機的具有不同幾何形狀的葉片進行建模，將所得的葉輪模型導入Creo Parametric軟件，在軟件Creo Parametric中，對離心風機的蝸殼進行建模。所選擇的離心風機的模型為板型模型，葉片數量為9，其初始模型如1所示。離心風機中蝸殼對于離心風機的影響也是十分巨大的[13-16]，由于主要研究離心風機葉片幾何形狀對離心風機整體性能的影響，所以在Creo Parametric中對蝸殼采用了簡單的建模方法，簡化后的模型如圖2所示。

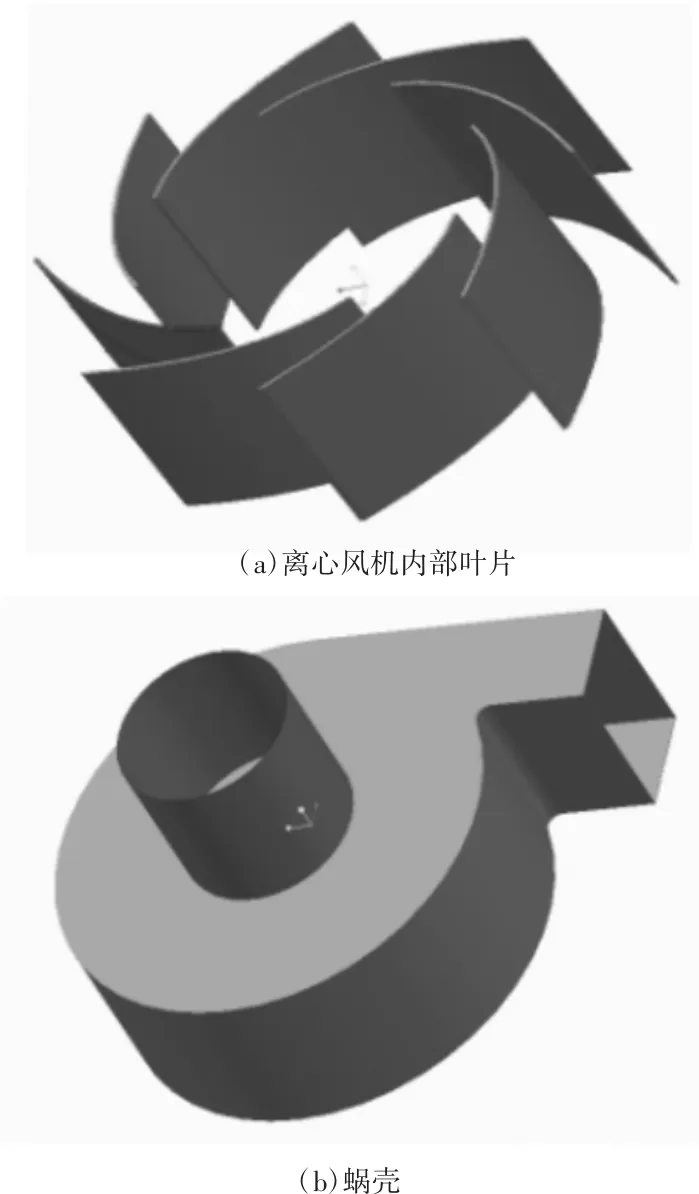
圖1 離心風機幾何模型

（續下圖）

（續上圖）

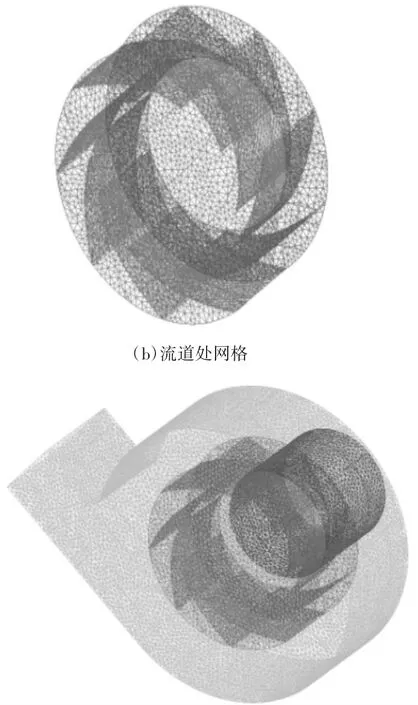
圖2 計算域網格模型

使用ICEM軟件對計算域模型進行網格劃分，使用非結構化網格生成方法，使用四面體和六面體網格相互組合的方式來進行網格的劃分工作，這樣不僅可以保證網格的質量還可以簡化計算和節省計算機的內存[17，18]。網格數量控制在200萬。如圖2為計算域的網格劃分情況。

2.2 邊界條件

采用理想可壓氣體，環境壓力選取為1個標準大氣壓，溫度選擇為288 K.進出口及壁面處邊界條件設定如下：

進口：即離心風機模型的進口，采用流量進口條件，選取進口流量為0.8 kg/m2，流動方向選擇沿壁面流動。

出口：即離心風機模型的出口，采用壓力出口的條件，選取表壓為300 Pa，流動方向選擇沿壁面流動。

連接面：將區域之間的連接面設置為interior.

葉輪流體區域：將葉輪流體區域采用移動類型為MRF，即設置為Frame Motion，轉速設置為2 900 r/min.

3 數值模擬結果分析

離心風機原型模擬：離心風機原型葉片形狀為板型葉片，葉片數目為9，進口角度為14°，出口角度為34°，葉片形狀由CFturbo自行生成，與蝸殼進行組裝后進行模擬和分析。圖3為軸向方向1/4位置和3/4位置處的離心風機的內部速度矢量圖。兩個位置的氣體的流動狀態相似，氣體通過葉輪做功速度得以提升，在蝸殼內經過減速擴壓之后速度下降從蝸殼出口流出，但是1/4處的氣體的流動速度較3/4處要高，所以導致了在蝸殼出口處產生了不同的結果，3/4處的氣流出口處產生了渦流，影響了整機的效率，并且通過自上而下的各個截面的觀察，發現越在蝸殼出口處的下部，其渦流越明顯，對離心風機進出口總壓的提升有較大影響。

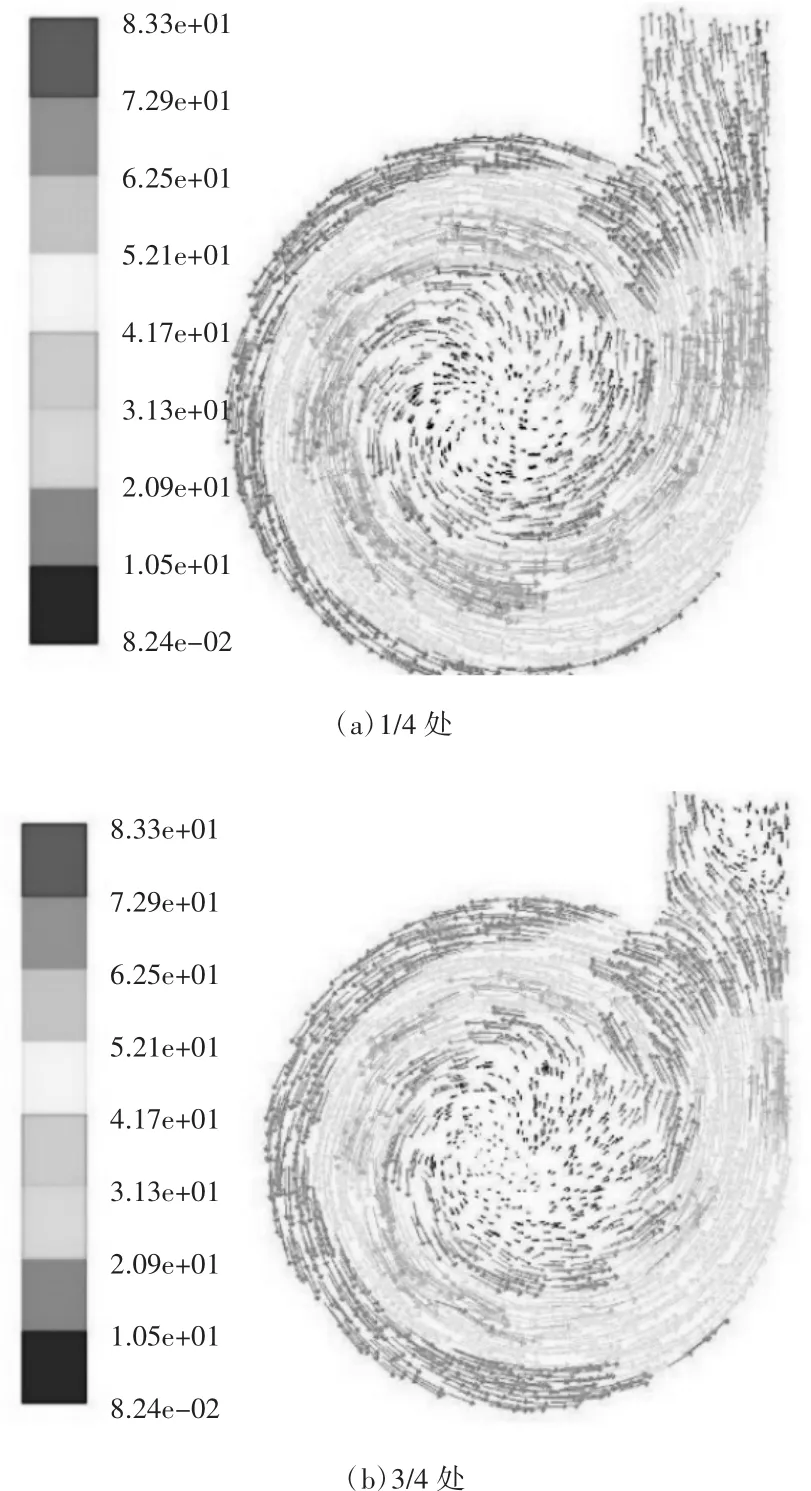
圖3 軸向速度矢量圖

圖4 是離心風機葉片表面的壓力分布圖。葉片在總壓方面葉片的吸力面和壓力面都隨著流動方向逐步提高，葉片壓力面總壓的數值高于吸力面的總壓數值，這也是葉輪做功的標志，葉輪的吸力面的總壓提高沒有壓力面總壓提高的幅度大，壓力面的總壓提高較為快速。從葉輪整體看，流動狀況良好。靜壓方面與總壓所得出的結論基本相同，在葉片的尾部所承受的壓力最大，偏轉的角度由于設計原因也越大，所以尾部比較容易出現氣流分離和應力問題[19-23]。

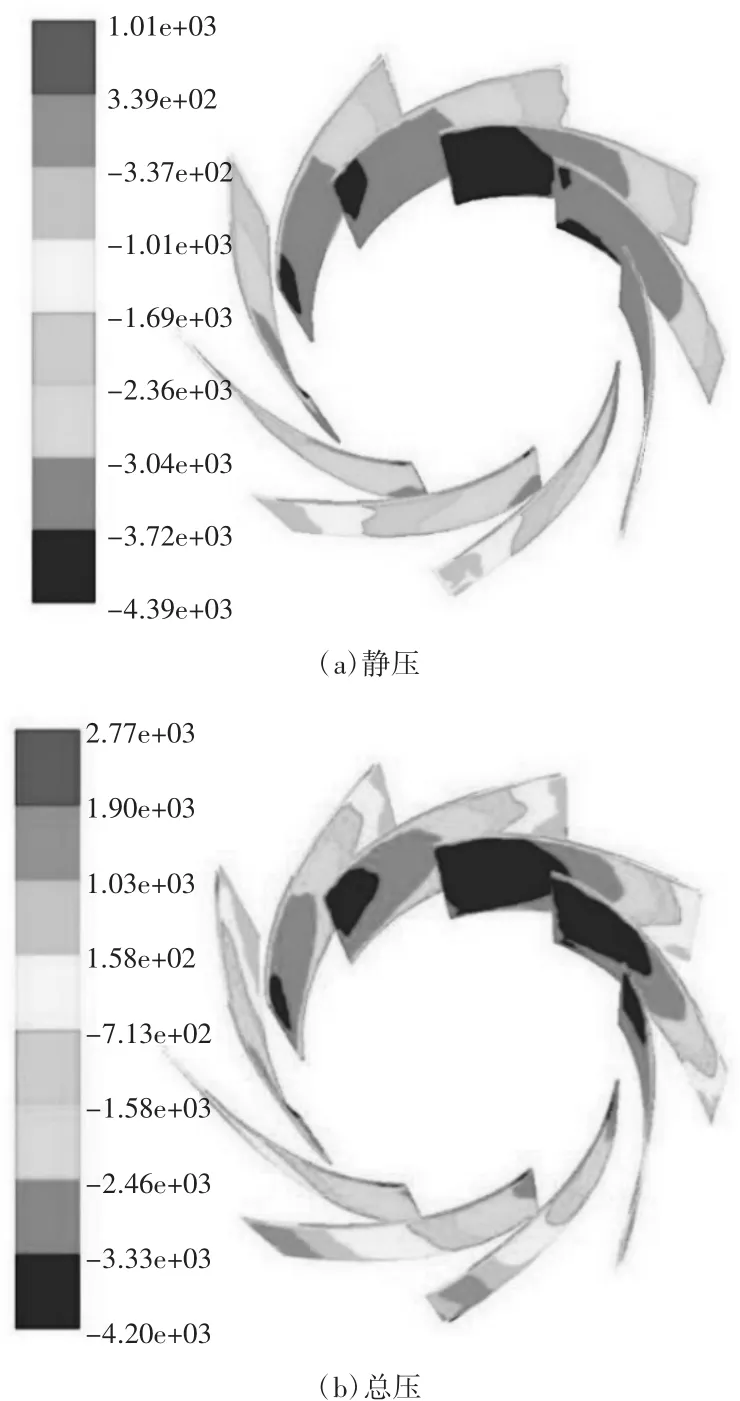
圖4 葉片壓力分布

4 不同葉輪參數模擬結果分析

通過分析原型機的內部流場情況，更改葉片的進口角、出口角及葉片的數量來對離心風機的性能參數進行計算分析，并結合計算結果提出離心風機的優化方案。

4.1 不同出口角下的模擬結果分析

葉片為原始進口角度為14°，出口角度為34°的板型葉片，在葉輪保持不變，葉片的進口角度也保持不變的情況下，將出口角度分別更改為30°，32°，36°和38°，并計算得到離心風機在不同流量下的總壓和效率分布與原型機的對比如圖5~圖6所示。

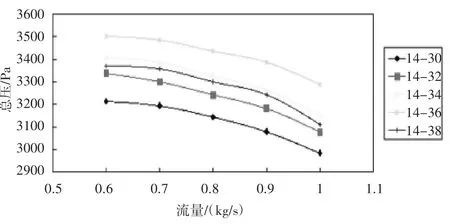
圖5 總壓特性線

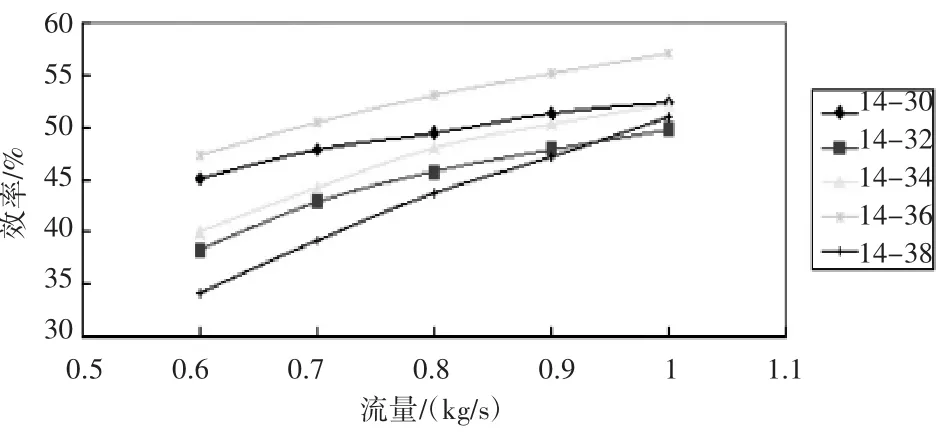
圖6 效率特性線

選擇5個工況點對出口角度不同的離心風機的模型進行模擬，分別對離心風機的總壓提升和效率進行計算和分析。根據流量總壓特性線可知，各個葉片出口角度雖然不同，但是總壓的變化規律相似，總壓伴隨著流量的增大逐漸減小。在總壓的大小方面出口角度為36°的離心風機的總壓在全工況下都優于葉片出口角度為34度的離心風機原型，可以認為將離心風機葉片出口角度更改為36°是對離心風機總壓方面進行了優化。

圖6為流量-效率特性線，從圖中可以看出，在全部工況下，30°出口角度的離心風機和36°出口角度的離心風機的效率優于34°出口角度的離心風機原型，可以得出結論，將離心風機出口角度更改為30°和36°的對于離心風機的效率進行了優化。與總壓分析相比較可知，出口角度為36°的離心風機改型在效率和總壓上都優于母型。

4.2 不同進氣角下的模擬結果分析

保持葉片數量和出口角保持與原型機相同，將進口角度分別更改為 12°，16°，18°和 20°，分別采用不同工況對離心風機進行數值模擬，得到其總壓與效率特性線，如圖7和圖8所示。

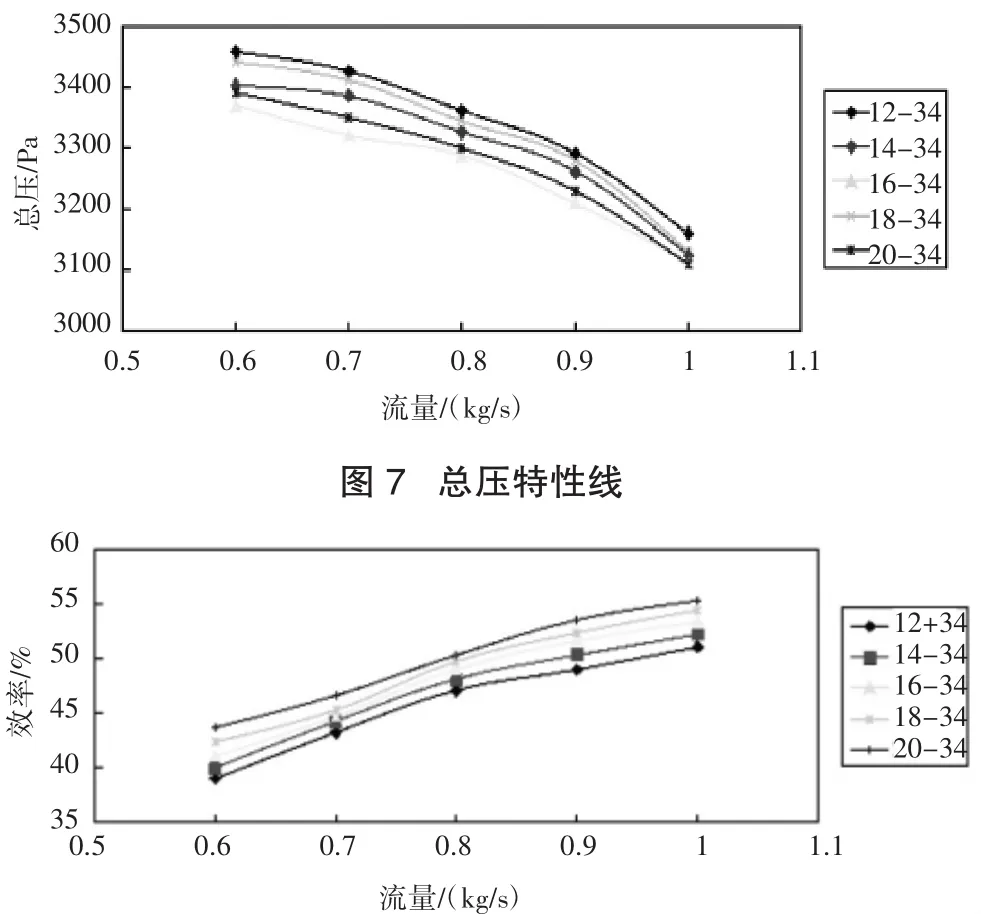
圖8 效率特性線

由總壓線可知，在進口角度有一定程度的更改的程度下，離心風機的總壓變化程度很小，整體變化趨勢可以由圖表相得出，可以得出在本文模型的前提下，改變離心風機葉輪葉片的進口角度，對離心風機整體的總壓提升影響較小，改變離心風機葉輪葉片進口角度的大小對離心風機總壓提升的優化并無太大意義。并且結合前文的處理和分析可知，葉片進口角度的更改對于離心風機內流場的流速，靜壓等參數等與原型相比較影響也較小。由效率線可知，離心風機的效率與葉片的進口角度有關，進口角度越大，離心風機的效率有所提高，但是提高的幅度不太大。

4.3 不同葉片數量下模擬結果

保持進、出口角不變，采用不同的葉片數目對離心風機進行數值模擬，更改葉片數目分別為7和8個。得到離心風機的總壓特性線如圖9.由總壓線分析可知，隨著葉片數目的增加，總壓的有所提升，得出的結論與前文分析一致，即隨著葉片數目的增加，離心風機的總壓有所提升，離心風機的靜壓隨著葉片數目的增加有所下降。

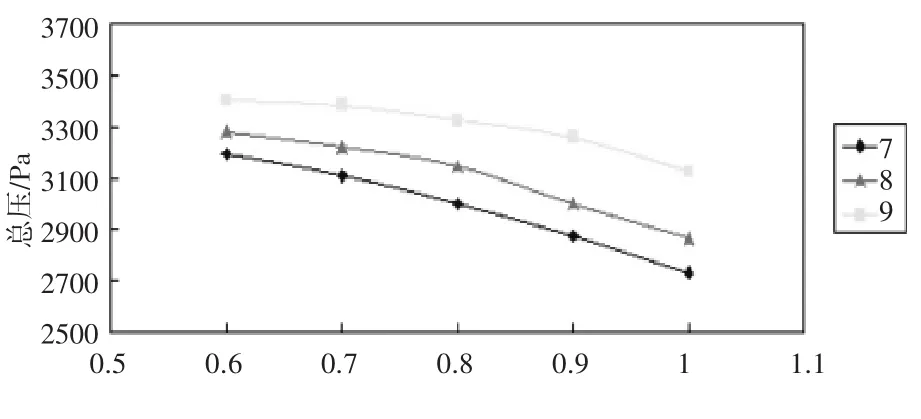
圖9 總壓特性線

5 結論

本文使用FLUENT通過更改離心風機葉片進口角、出口角和葉片數目種方法來模擬離心風機的性能變化，通過分析模擬計算結果可以發現，在單一工況的條件下，隨著出口角度的增大，總壓和效率總體上呈現先增大后減小的變化趨勢，并且在出口角度為36°的葉型的離心風機中，總壓和效率取得最大值；進口角度的改變對離心風機總壓和效率的影響存在，但是不是特別明顯，通過特性線分析可知，總壓變化幅度和效率變化幅度存在微小的改變；通過葉片數目的改變，對離心風機進行分析可知，隨著葉片數目的增多，離心風機的總壓和效率有明顯的提升，并且在葉片內的靜壓有所降低，葉片數目的增多可以在一定程度上優化離心風機的總壓和效率。

[1]劉 強，王發展.離心風機內部流場研究的現狀與展望[J].礦山機械，2011（13）：33-34.

[2]劉瑞韜，徐 忠.離心葉輪機械內部流動的研究進展[J].力學進展，2003，33（4）：518-532.

[3]席 光，王志恒，王尚錦.葉輪機械氣動優化設計中的近似模型方法及其應用[J].西安交通大學學報，2007，41（2）：125-135.

[4]鄧建鋼，辛大蘭，肖云峰，等.離心風機數字化設計與實驗研究[J].風機技術，2013（04）：40-43.

[5]張顧鐘.離心風機優化設計方法研究[J].風機技術，2011（05）：26-30，44.

[6]韓占忠.FLUENT流體工程仿真計算實例與應用[M].北京：北京理工大學出版社，2004：112-123.

[7]王福軍.計算流體動力學分析[M].北京：清華大學出版社，2004：150-164.

[8]徐長棱，毛義軍.離心通風機整機三維流場的數值模擬[J].風機技術，2005（05）：15-18.

[9]譚大治，袁 新.高精度高分辨率格式模擬離心葉輪內湍流流場.汽輪機技術[J].2003，45（3）：139-141.

[10]蔡睿賢，張 娜.理想氣體非定常有摩擦有傳熱一維流動的顯式波動解析解[J].工程熱物理學報，2002（2）：184-185.

[11]李曉麗，楚武利，袁 森.離心風機整機三維數值仿真方法及分析[J].計算機仿真，2010，27（10）：335-338，365.

[12]姜 華，宮武旗，張 煒，等.帶分流葉片離心葉輪非定常流場的實驗研究[J].西安交通大學學報，2009（9）：14-15.

[13]朱宏磊，李意民，孫更生，等.后蓋板傾角對離心風機磨損影響的實驗研究[J].礦山機械，2005（12）：28-29.

[14]李 凱，曹淑珍，劉正先.離心風機葉片擴壓器內部流場的實驗研究[J].流體機械，2005（3）：1-2.

[15]楊 詠，楚武利，吳艷輝，等.后置蝸殼斜流風機整機數值模擬[J].風機技術，2006（60）：1-4.

[16]孫長輝，劉正先，王 斗，等.蝸殼變型線改進離心風機性能的研究[J].流體機械，2007，35（4）：1-5.

[17]余志鵬.軸流風機與橫流風機串聯工作時風機之間氣流特性的研究[D].洛陽：河南科技大學，2001.

[18]張 莉，陳漢平，徐 忠.離心壓縮機葉輪內部流場的準三元迭代數值分析[J].風機技術，2000（5）：25-29.

[19]沈遠勝，劉高聯，劉永杰.三維管道內有旋流動的渦勢函數擬變分原理[J].應用數學和力學，2004（1）：9-10.

[20]王松嶺，雷 泳，李春曦，等.電廠離心風機容積損失的數值分析[J].華北電力大學學報，2006，33（1）：60-63.

[21]李海鋒，吳玉林，趙志妹.利用三維紊流數值模擬進行離心葉輪設計比較[J].流體機械，2001，29（9）：18-20.

[22]王松濤，丁 俊，姜 斌，等.三維葉片技術對離心風機流場結構的影響[J].機械工程學報，2014，50（04）：178-184.

[23]丁 駿，杜 鑫，姜 斌，等.三維葉片技術對離心風機流場性能的影響[J].中國電機工程學報，2012，32（32）：109-115.