基于幅相聯合信息的目標檢測方法

,

(中國電子科技集團公司第三十八研究所,安徽合肥230088)

0 引言

在雷達目標檢測中,特別是實戰情況下,常會遇到大目標遮擋小目標的問題。一般地,大型民航客機的RCS在一二百平方米以上,小型戰斗機的RCS在1～2 m2之間。如果兩者的距離很近,則回波的強度比則在20 dB以上。如果考慮到隱身飛機等更小的RCS(其RCS只在0.02 m2左右)目標,回波強度相差40 dB以上,遮擋問題將更加嚴重。

在民用航空機場管理領域,通過采用非線性調頻超低副瓣脈壓技術[1],并輔之以嚴格的管理措施,來解決大型客機對小型客機的遮擋問題。然而,在軍用領域,在更加復雜的空情處理上,這種問題更加復雜——敵機可能是故意躲在民航機下造成遮擋,也難以使用空管措施。如果抬高門限,則會將小目標剔除。如果降低門限,則大目標會出現多個連續的過門限值,一般采用點跡凝聚技術或雜波圖,小目標往往會被視作大目標的副瓣而匿隱掉,如果采用CFAR技術,小目標也將會被門限遮掉。此時,將會出現漏情。在復雜的軍事斗爭條件下,應解決這種利用大型目標遮擋效應的突防問題。

1 大目標遮擋效應分析

圖1為兩個相距2個距離單元的目標回波仿真圖。從圖中可以看出,由于目標回波具有一定的寬度,兩個目標的回波幅度相差較遠。在進行距離凝聚時,目標2會被當成目標1的副瓣而凝聚掉,檢測結果只有目標1出現,而目標2造成漏警。局部放大圖如圖2所示,假定目標1與目標2的信噪比差距為25 d B——普通戰斗機與大型民航客機的回波幅度差異(假定民航客機的雷達截面積為300 m2,戰斗機的雷達截面積為1 m2)。目標1是一個大型目標,目標2是一個小型目標。雷達發射的信號為線性調頻信號。在正常情況下,必然會將目標2當作目標1的副瓣,目標2將被凝聚掉,因而會造成漏警。

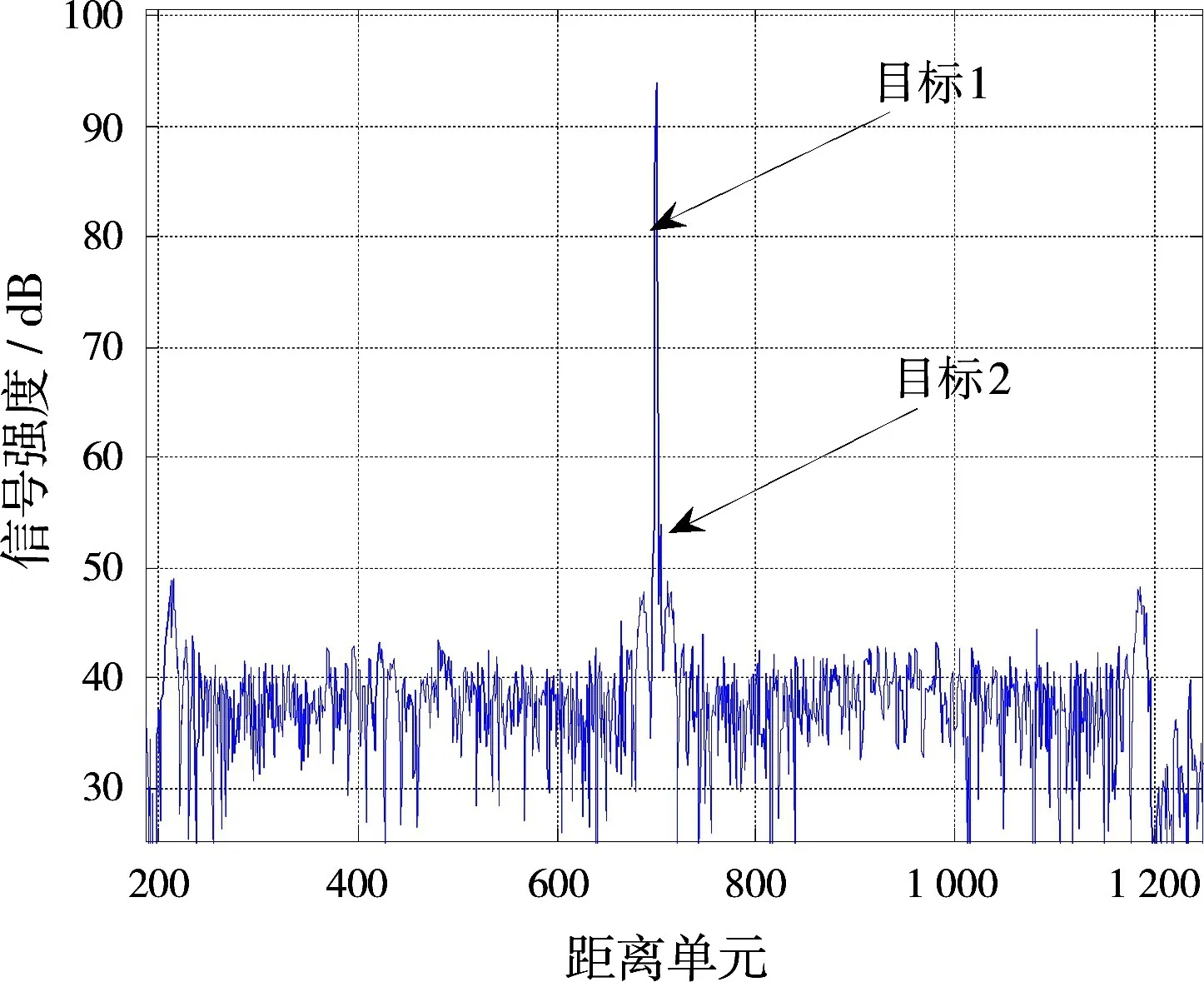
圖1 兩個相距2個距離單元的目標

圖2 大小目標相近時的回波信號

造成這種問題的原因是常規檢測不考慮相位,僅利用幅度信息。另外在檢測過程中存在一個點跡凝聚步驟。點跡凝聚[2]是在距離項上的距離凝聚處理、方位項上的方位凝聚處理、仰角項上的目標測高處理、速度上的解模糊處理等。凝聚的主要原理為對幅度過門限的單元判別連續性,取包絡峰值。主要完成相同極值點的提取,產生極值點的代碼、極值幅度。總之,傳統的凝聚算法利用的核心信息是幅度。顯然,這對原始信號的信息進行了刪減,幅度信息必然會受到信噪比效應的影響,對目標的檢測造成損失。如果采用CFAR處理也達不到檢測目標的目的,因為小目標位置與大目標的距離太近。試驗結果如圖3～圖5所示。

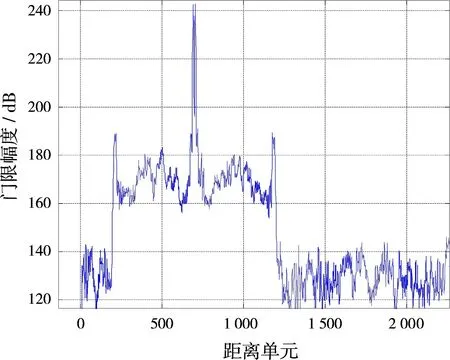
圖3 回波CFAR門限圖

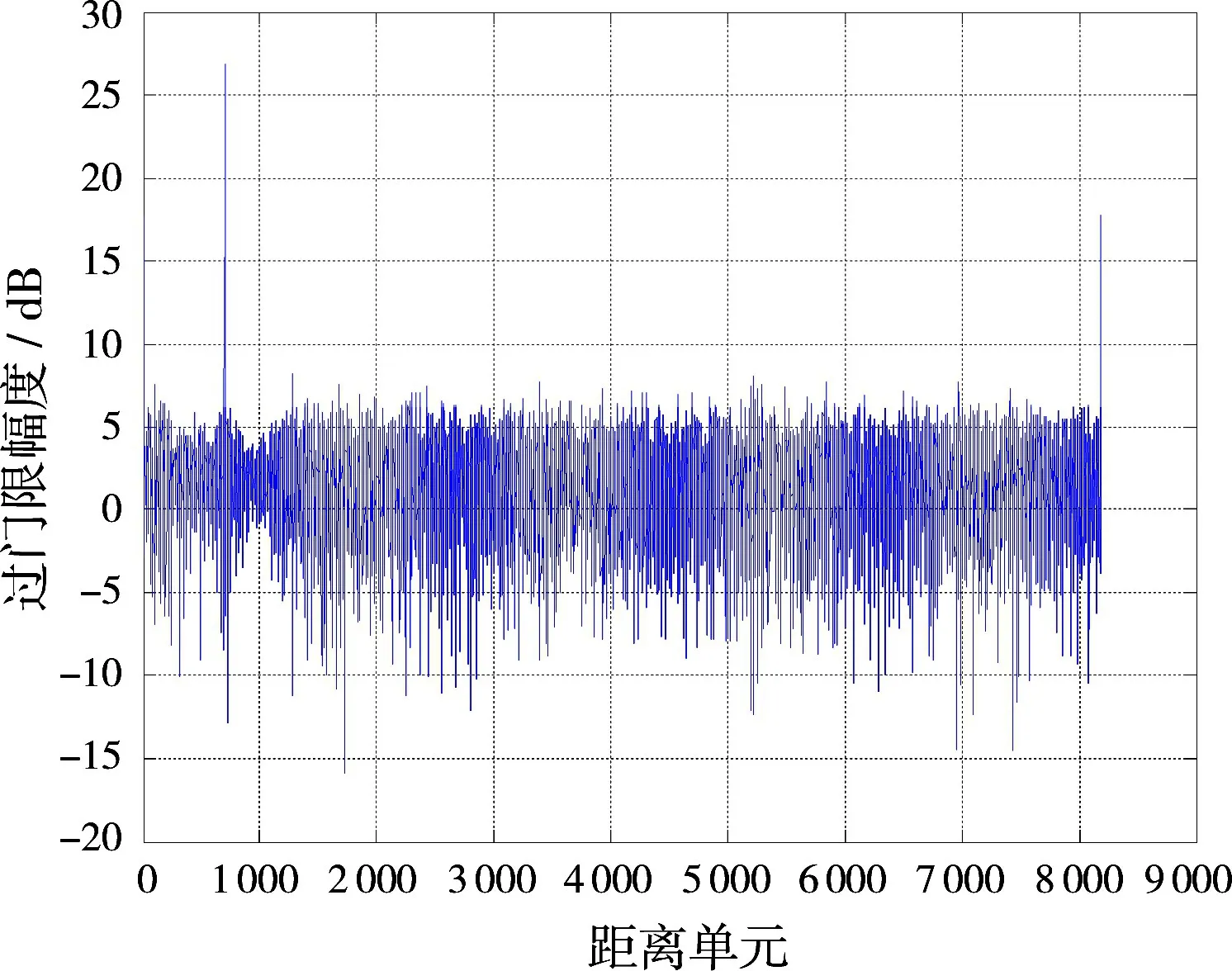
圖4 目標相距2個距離門過CFAR門限信號

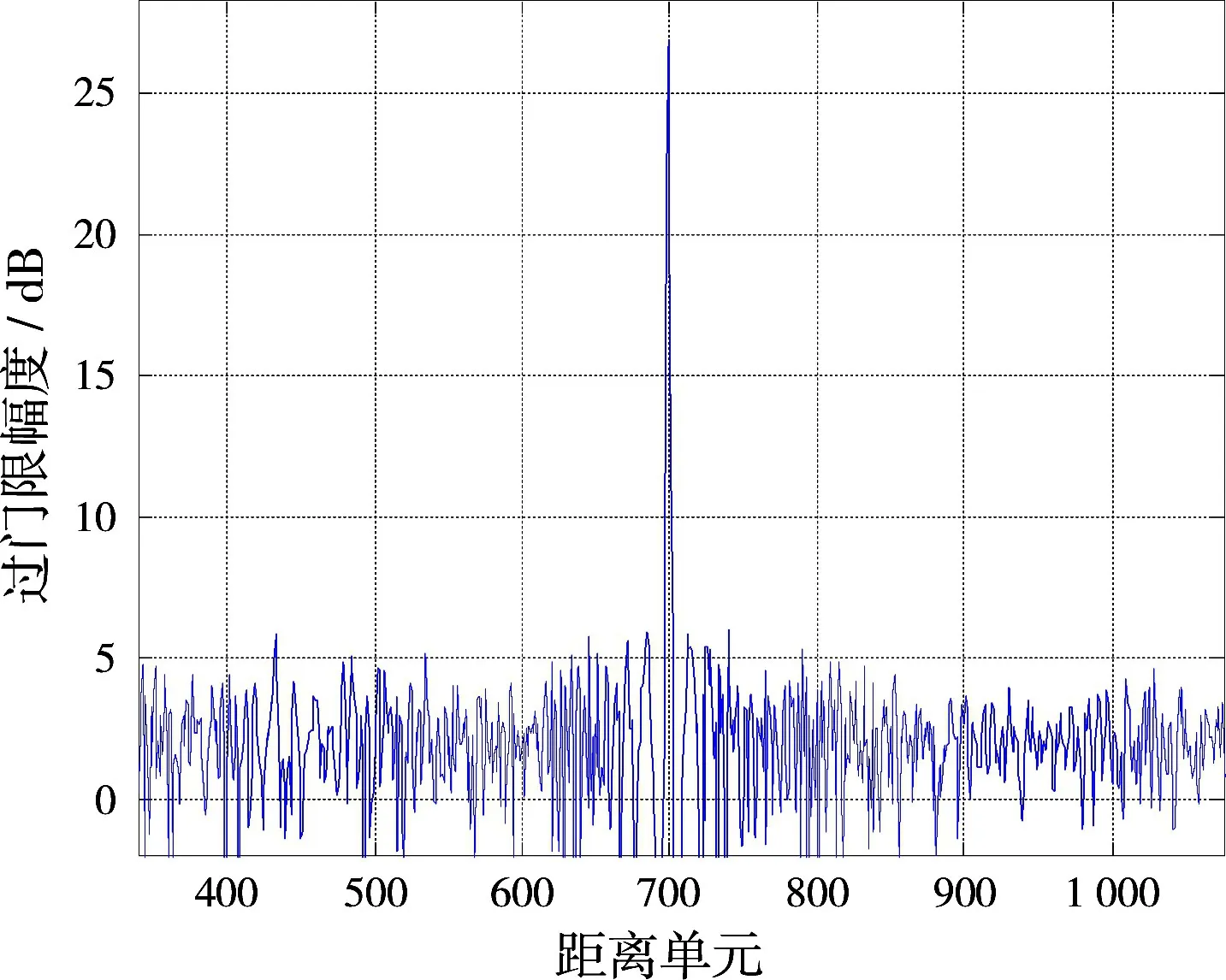
圖5 回波過CFAR門限信號(局部,距離2個單元)

當小目標距離大目標距離單元為10個以上時,目標可以通過CFAR提取出來,如圖6所示。圖7為局部放大圖。

產生這個問題的根本原因是:兩目標的信噪比相差太大,且距離太近。在如此近的條件下,如果兩回波幅度存在數量級的差別,必然會造成小目標被“忽視”的問題。

如果嚴格限制信號的副瓣電平,當信號主要能量集中在主瓣時,則需要進行深度加權,此時會造成主瓣顯著加寬,對小目標的遮擋更加嚴重。同時,這種處理辦法需要信號的時寬帶寬積很大,加大了工程實現難度。如果采用非線性調頻進行優化設計,則會由于多普勒效應、噪聲等影響,難以實現[1]。

造成上述問題的主要原因是幅度差異太大,如果僅考慮幅度信息比較必然會造成遮擋。根據理論分析,對于目標而言,不僅有幅度信息,而且還有相位信息,并且主瓣的相位與副瓣的相位特性差別很大。這將為目標檢測提供一個新的途徑。

在傳統的雷達信號處理中,為了減輕處理的負荷,僅考慮目標回波的幅度信息,如果要考慮相位信息,則系統的存儲、處理的負擔會大大增加。隨著現代信號處理,特別是存儲技術、軟件化技術的發展,處理器的速度及容量都得到了顯著的提升,將相位信息引入到目標檢測中來,已完全可行。利用目標回波的主瓣與副瓣相位性質的不同來檢測目標的存在,可以改善大目標對小目標的遮擋問題。

2 基于聯合幅相信息的目標檢測算法

現代雷達主要采用的是匹配濾波[3]。在信號處理中利用的是匹配濾波器。該種濾波器為白噪聲背景中檢測信號的最佳線性濾波器,其準則為信噪比最大原則。

假定雷達發射信號的s(t),其頻譜為S(ω),則匹配濾波器的頻響為H(ω),回波的頻域表示為

式中,t0為信號達到最大的時刻。

匹配濾波的響應輸出可由下式給出[4]:

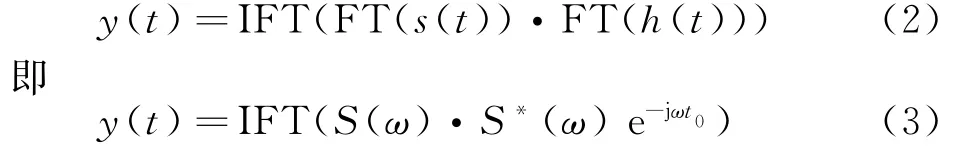
當信號與濾波器完全匹配時,式(3)可以寫成

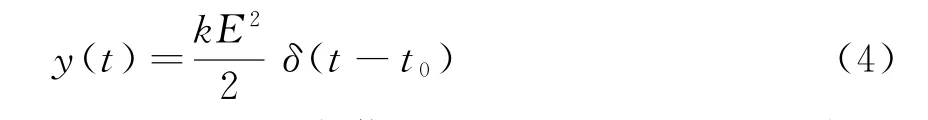
式(4)表明,當信噪比達到最大時,相位為零。反之,如果離開了t0位置,則信號的能量會急劇減小。由于噪聲的影響,其相位不會為零,并表現出隨機性。如果采用脈壓的形式,則副瓣的相位也將表現為隨機變化性。如下:

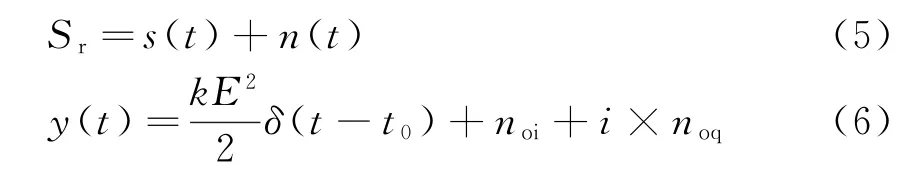
根據式(6),在信號噪聲比較大的情況下,在匹配濾波器與回波完全匹配時(距離完全對齊時),可以得到y(t)的相位為趨于0。當信號與噪聲相當時,相位趨于26.5°,因此,建議當目標起伏小于30°時,可鑒定為主瓣。對于數字化的線性調頻信號,由于相位為二次型,在序列未完全對齊時相位變化極大,圖8為線性調頻的相位曲線圖。通過圖8可以看出如下特點:

1)調頻信號的相位是對稱的,在反轉條件下,相位圖形不變;

2)卷積的本質為乘加,當匹配濾波器與信號完全匹配時,其結果是相位相加,幅度相乘,故而相位為0,幅度最大;

3)在相位絕對值最大時,相位變化率為0,即幅度最大值附近的相位是平坦的。

因此,在最大值左右兩側的相位變化必然很小。脈壓后的相位平坦點至少有連續3個。幅度加權不影響該性質。

同樣,脈壓波形在最大值3點以內,目標的回波相位基本不變,起伏較小,在信噪比足夠大時,近似一條水平線,而在此之外,相位呈現隨機變化的情況。本文采用相位差分的方法進行相位起伏性評估。所謂相位差分指的是相鄰兩點的相位相減。

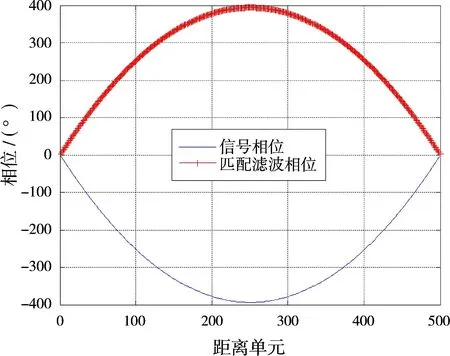
圖8 線性調頻波形與匹配濾波器相位

圖9為某雷達時寬帶寬積為500時,采用Taylor窗進行脈沖壓縮的幅度響應;圖10為相位響應。圖11為圖10的局部放大圖。

從圖11可以看出,在脈沖壓縮信號的主瓣處一定有一段相位平坦區。一般這個平坦區集中在主瓣3 d B寬度附近,根據采樣率情況,一般為3點以上。另外,由于幅度加權造成脈壓信號的一部分出現相位變化較慢區域,但這一部分是在遠離主瓣的地方,同時,也不會出現連續多點相位基本不變的情況,因此,可以通過幅度信息將其濾掉。

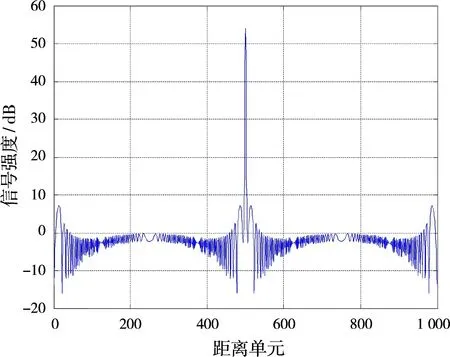
圖9 線性調頻信號脈壓幅度輸出

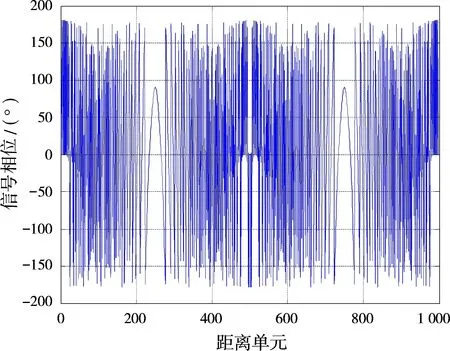
圖10 線性調頻信號脈壓相位輸出

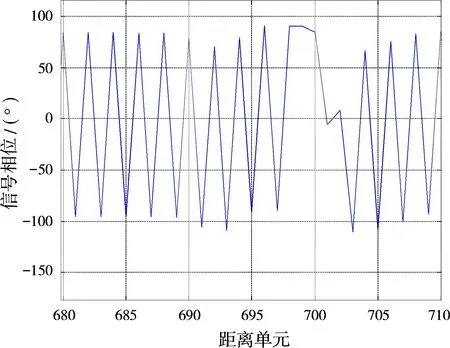
圖11 線性調頻信號脈壓相位輸出(主瓣附近)

綜上所述,基于幅相聯合凝聚的算法,引入了相位指示的辦法,具體如下:

1)檢測時,除了需保留回波的幅度以外,還應保留回波的相位信息,特別是當某一目標強度很大,則對其脈壓結果主瓣左右兩側可取若干個點進行相位檢測,評估其平坦度,一般采用行相位差分辦法。

2)幅相聯合檢測算法中,在利用相位差分評估目標相位變化時。相位起伏可采用前后求差分的方式,一般大目標主瓣有兩個平坦值(差分值很小),被遮擋的小目標主瓣只有一個平坦值(如果小目標離大目標較遠,則有兩個平坦值)。

3)相位檢測算法為相位窗口,窗口長度一般取3個,如果為超采樣應相應延長,如為兩倍采樣時,窗長度取為5個,依次類推。

4)相位窗內目標的相位起伏(一般應小于30°)較小時,則該點即可能是個小目標,應予保留。

5)如果目標回波較小,不建議采用幅相聯合檢測方法,以防止虛警增加。

3 仿真分析

圖12(a)為相位差分結果;圖12(b)為相位差分結果局部放大圖;圖12(c)為蒙特卡洛仿真的試驗結果[4],仿真次數為10 000。圖13為目標距離2個距離門目標的回波的相位差分試驗結果。本例中,小目標的信噪比為9 d B,其相位變化為28.6°～41.5°。

圖12(b)為存在2個目標時的相位差分圖。根據試驗情況分析,對于大目標,存在2個距離單元的相位平坦點,對于小目標存在1個相位平坦點,經分析為大目標干擾造成。在圖12(b)中,由于左側處于大目標的相位干擾區,使得小目標的相位受影響。在右側,大目標的信號小于小目標的信號,因此干擾不會影響小目標在右側的相位特性(或對右側的相位特性影響較小),小目標的相位平坦點將減少為2個,差分時僅為一個點,仍可精確獲取該位置處的相位差分值。

圖12(c)為蒙特卡洛仿真10 000次試驗中,對小目標的相位差分的觀察結果。

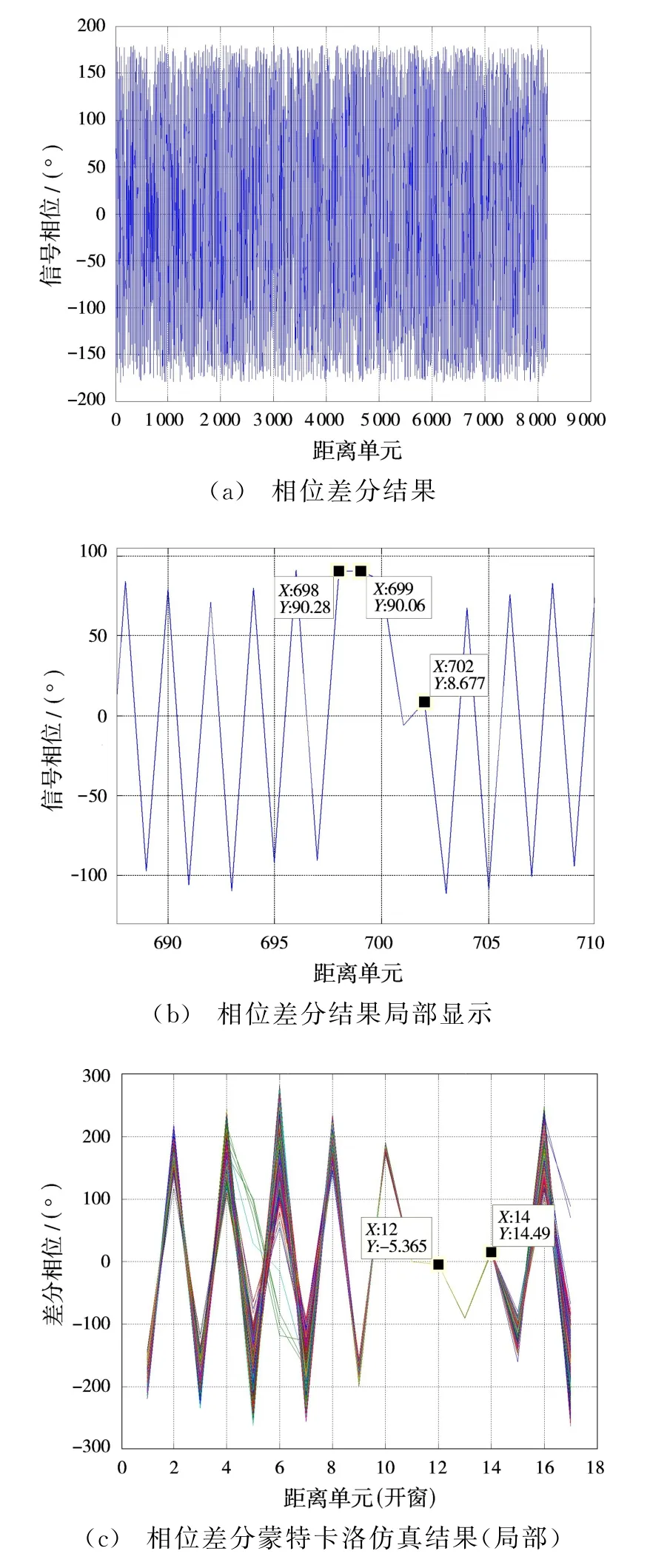
圖12 目標附近差分相位圖

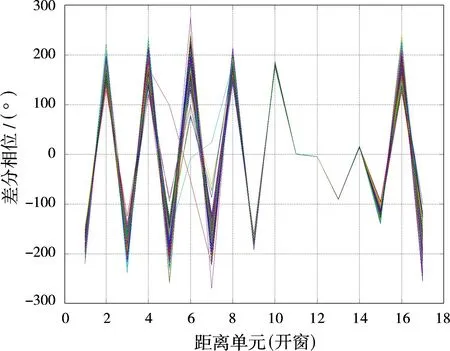
圖13 小目標信噪比從9 dB增加到15 dB時的相位變化率

從圖12(b)、圖12(c)可以看出,目標所在地方不光相位變化幅度小,而且相位變化基本上是穩定在一個特定值。該值受信噪比影響,當信噪比很大時,目標相位起伏小,反之變大。

圖13為目標信噪比從9 dB變化到15 dB(變化1 000次)時,相位差分的變化結果。從圖13可以看出,當目標信噪比從9 d B變化到15 dB時,相位差分的變化率為14.5°～34.5°,小目標的信噪比越大,則相位穩定性越強。

4 結束語

本文算法適用于大目標遮擋小目標時對小目標的檢測。此時,要求小目標具有一定的信噪比;如果信噪比遠小于副瓣,則難以檢測。另外,如果小目標處于雜波區中時,也可以利用該辦法解算出小目標,由于雜波區很大,可能會存在于目標的左右兩側,因此,此方法對于雜波中目標的檢測效果要低于在大目標處的效果[5]。通過加權算法,脈壓主瓣點的相位存在一個平坦區,而其余地方相位會出現極大的跳變,即目標主瓣的相位跳變是緩慢的,而副瓣的跳變是劇烈的。可據此判斷目標的存在與否。但這種算法會帶來新的虛警(取決于個位門限),但會將漏警率大大減小,此時,可以通過邏輯的方法將之消除[6]。

非線性調頻信號及相位編碼信號滿足本文相位檢測的前提條件,因此,非線性調頻信號可以利用相位檢測的方法。未采用脈壓技術的信號波形不適用于本算法,但可用超采樣技術,獲得相位差分值。相位信息的有效性受噪聲影響極嚴重[7],這是由于噪聲將會對信號矢量造成干擾使之偏離了初始指向,因此,會帶來相位失真[7-8]。該算法的抗噪聲性能有待于進一步分析。根據試驗仿真,一般信噪比不應低于7 d B。

[1]付啟眾,陳忠先.一種超低副瓣非線性調頻脈壓性能分析[J].雷達科學與技術,2007,5(1):60-64.

[2]雷遠宏.地面常規體制下的點跡凝聚算法分析[J].硅谷,2012(7):177-178.

[3]SKOLNIK M I.雷達系統導論[M].3版.左群聲,徐國良,馬林,等譯.北京:電子工業出版社,2012.

[4]PROAKIS J G,SALEHI M,BAUCH G.現代通信系統:MATLAB版[M].2版.劉樹棠,譯.北京:電子工業出版社,2005.

[5]皇甫一江,付啟眾,徐晉.雷達海雜波性能分析及消除方法[J].電腦知識與技術,2013,9(5):1177-1179.

[6]CARLSON B D,EVANS E D,WILSON S L.Search Radar Detection and Track with the Hough Transform,Part I:System Concept[J].IEEE Trans on Aerospace and Electronic Systems,1994,30(1):102-108.

[7]KAY S M.統計信號處理基礎:估計與檢測理論[M].羅鵬飛,張文明,劉忠,等譯.北京:電子工業出版社,2011.

[8]唐小文,李榮鋒,戴凌燕,等.自適應副瓣對消與動目標檢測的聯合使用[J].雷達科學與技術,2014,14(3):273-278.