聚焦圓的最值的交匯問題

■宋全會 趙 昆

聚焦圓的最值的交匯問題

■宋全會 趙 昆

圓是高中解析幾何的重要內容，圓的最值問題又是高考考查的重點內容，且常常和高中數學的其他知識交匯考查。下面就圓的最值的交匯問題，進行分類解析，以加深同學們對此類問題的理解與應用。

一、圓與定點的交匯問題

1.圓外一定點到圓上一動點距離的最大值與最小值問題

例 1 已知點M（—l，2），點N 在圓C：（x—2）2+y2=9上，求的最大值和最小值。

解：由圓C：（x—2）2+y2=9，可知圓心C2，0（），半徑R=3。

方法歸納：設圓外一點M 到圓心為C、半徑為R的圓上的點N的距離為d，則dmin

如圖l，過點P的直線AB⊥PC，其中A，B是直線與圓的交點，則線段AB即為所求的最短弦。

由于△APC為直角三角形，且|AC|=R=2，|PC|=

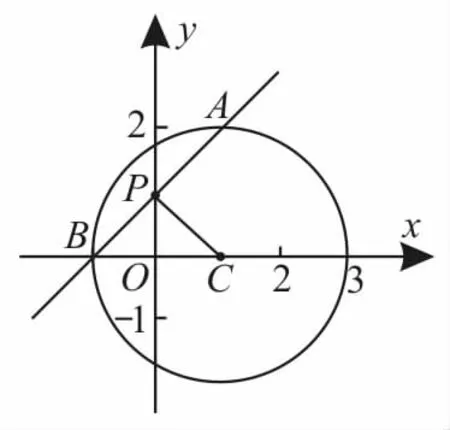
圖l

2.過圓內一定點的最長弦和最短弦問題

例 2 已知點P（0，l）在圓C：（x—l）2+y2=4的內部，則過點P的直線被圓截得的最長弦與最短弦分別為____。

解：依題意可得，最長弦為圓的直徑，即弦長為4。

方法歸納：經過圓內的點且過圓心的弦即為最長弦（直徑），與最長弦垂直的弦是最短弦。

二、圓與直線的交匯問題

1.圓上的動點到定直線的距離的最大值和最小值問題

例 3 圓C：x2+y2—2x—2y+l=0上的動點M 到直線x—y—2=0的距離的最大值是（ ）。

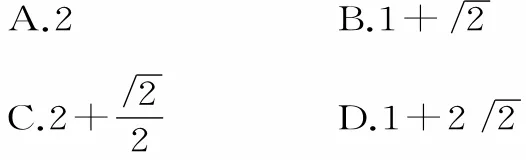
解：圓x2+y2—2x—2y+l=0的圓心C（l，l），半徑R=l，則圓心C到直線x—y—2=0的距離

故圓x2+y2—2x—2y+l=0上的動點M 到直線x—y—2=0的距離的最大值為d+R =l+。應選B。

方法歸納：若C為一定點，P是一條直線上的動點，則 PC 的最小值就是定點C到該直線的距離。

2.過定直線上的動點作圓的切線，求切線長的最小值問題

例4 過直線y=x+l上的任一點向圓C：（x—3）2+y2=l引切線，則切線長的最小值為（ ）。

解：如圖2所示。設直線上的任一點為P，切點為Q。由題意可知圓心為C（3，0）。

由PQ為切線，可知 PQ⊥CQ，|CQ|=R=l，可得切線長|PQ|=所以當|PC|的值最小時，|PQ|取得最小值。

圖2

由題意可知，|PC|的最小值為圓心C到直線y=x+l的距離，所以

方法歸納：|PC|的最小值即為圓心到直線的距離，因此可借助點到直線的距離公式求得。

三、圓與圓的交匯問題

1.兩圓上動點的距離的最大值與最小值問題

例 5 點P 在圓Cl：x2+y2—8x—4y+ll=0上，點Q 在圓C2：x2+y2+4x+2y+l=0上，則的最小值為（ ）。

解：圓Cl：x2+y2—8x—4y+ll=0的方程可化為（x—4）2+（y—2）2=9，所以圓Cl的圓心Cl（4，2），半徑Rl=3；圓C2：x2+y2+4x+2y+l=0的方程可化為（x+2）2+（y+l）2=4，所以圓C2的圓心C2（—2，—l），半徑R2=2。

方法歸納：圓Cl的半徑為Rl，圓C2的半徑為R2，圓Cl上的動點為M，圓C2上的動點為N，則

2.直線上的點到兩圓上的點的距離的最值問題

例6 已知M，N分別為圓Cl：（x—4）2+（y—l）2=4與圓C2：（x+l）2+（y—2）2=l上的點，P為直線l：y=x+l上的一點，則

解：圓Cl：（x—4）2+（y—l）2=4的圓心Cl（4，l），半徑Rl=2；圓C2：（x+l）2+（y—2）2=l的圓心C2（—l，2），半徑R2=l。

由圓心Cl，C2的坐標可知，Cl，C2位于直線l：x—y+l=0的兩側，如圖3所示。

設圓心C2關于直線l：x—y+l=0的對稱點為C3（x0，y0），則由對稱性可得方程組

圖3

所以圓C2關于直線l：x—y+l=0的對稱圓C3的圓心為C3（l，0），半徑R3=l。由對稱性可知

方法歸納：解決此類問題，首先要判斷兩點在已知直線“同側”還是“異側”，根據需要求其中一個點關于已知直線的對稱點，然后利用“同側和最小，異側差最大”求解。

四、與圓上點的坐標有關的交匯問題

例 7 已知點P（x，y）在圓x2+（y—l）2=l上運動，則的最大值與最小值分別為____。

點Q（2，l）連線的斜率。

所求問題可轉化為過定點Q（2，l）的動直線與圓有交點的情況下，求斜率k的最大值和最小值。根據圓的幾何意義知，當該直線與圓相切時，k取得最大值與最小值。

設過定點Q（2，l）的直線方程為y—l=k（x—2），即kx—y+l—2k=0。

2.形如z=ax+by的最值問題

例 8 已知實數x，y滿足方程x2+y2—4x+l=0，求y—x的最大值和最小值。

解：令z=y—x，則z看作是直線y=x+z在y軸上的截距。

已知方程x2+y2—4x+l=0為圓的方程，其圓心坐標為（2，0），半徑R=3。

當直線y=x+z與圓相切時，截距z取得最大值和最小值。由

方法歸納：形如z=ax+by的最值問題，可轉化為直線在y軸上的截距的最值問題。根據圓的幾何意義知，當直線與圓相切時，直線在y軸上的截距取得最大值和最小值。

3.形如D=（x—a）2+（y—b）2的最值問題

例 9 已知函數y=f（x）是定義在R上的增函數，函數y=f（x—l）的圖像關于點（l，0）對稱。若對任意的x，y∈R，不等式f（x2—6x+2l）+f（y2—8y）＜0恒成立，則當x＞3時，x2+y2的取值范圍是（ ）。

A.（3，7） B.（9，25）

C.（l3，49） D.（9，49）

解：由函數y=f（x—l）的圖像關于點（l，0）對稱，可得到函數y=f（x）的圖像關于點（0，0）對稱，由此可知函數y=f（x）為奇函數。

因為f（x2—6x+2l）+f（y2—8y）＜0，所以f（x2—6x+2l）＜f（8y—y2）。

又因為函數y=f（x）是定義在R上的增函數，所以x2—6x+2l＜8y—y2，可得（x—3）2+（y—4）2＜4，且x＞3。

所以點（x，y）所形成的區域可看作以C（3，4）為圓心，2為半徑的半圓內部，如圖4所示。

根據兩點間的距離公式，令D=x2+y2，則D=x2+y2可看作半圓（x—3）2+（y—4）2＜4，且x＞3的內部的點（x，y）到原點（0，0）的距離的平方。

圖4

由圓的幾何性質可知，當點（x，y）在半圓的B點時距離最大，即

當點（x，y）在半圓的 A（3，2）點時距離最小，即Dmin=3—0（）2+2—0（）2=l3。

由上可知，x2+y2的取值范圍為（l3，49）。應選C。

附言：本文系20l6年度河南省基礎教育教學研究項目《微課資源建設與應用研究》研究成果，課題編號：JCJYBl6250232。

河南開封高中

（責任編輯 郭正華）