具有非線性發(fā)病率的SIVS流行病模型的動(dòng)力學(xué)行為
,
(太原理工大學(xué) 數(shù)學(xué)學(xué)院, 山西 太原 030024)
具有非線性發(fā)病率的SIVS流行病模型的動(dòng)力學(xué)行為
曲美鋒,董玲珍
(太原理工大學(xué)數(shù)學(xué)學(xué)院,山西太原030024)
為了研究具有非線性發(fā)病率的SIVS流行病模型,在確定性模型中討論無(wú)病平衡點(diǎn)與地方病平衡點(diǎn)的存在性和穩(wěn)定性,給出基本再生數(shù)的表達(dá)式,并得出正平衡點(diǎn)穩(wěn)定的充分條件;引入隨機(jī)擾動(dòng),通過(guò)構(gòu)造適當(dāng)?shù)腖yapunov函數(shù),利用伊藤公式,研究相應(yīng)的隨機(jī)SIVS模型。結(jié)果表明:當(dāng)基本再生數(shù)小于或等于1時(shí),確定性系統(tǒng)有唯一的全局漸近穩(wěn)定的平衡點(diǎn),即無(wú)病平衡點(diǎn);當(dāng)基本再生數(shù)大于1時(shí),該點(diǎn)不穩(wěn)定,系統(tǒng)存在正平衡點(diǎn),即地方病平衡點(diǎn);如果因病死亡率滿(mǎn)足一定條件,當(dāng)基本再生數(shù)小于或等于1時(shí),隨機(jī)系統(tǒng)的無(wú)病平衡點(diǎn)全局隨機(jī)漸近穩(wěn)定,即疾病將會(huì)滅絕;當(dāng)基本再生數(shù)大于1時(shí),隨機(jī)系統(tǒng)的解在相應(yīng)確定性系統(tǒng)的地方病平衡點(diǎn)附近波動(dòng),并且波動(dòng)強(qiáng)度與白噪聲強(qiáng)度成正比,即白噪聲強(qiáng)度充分小時(shí),疾病將會(huì)盛行。
非線性發(fā)病率;無(wú)病平衡點(diǎn);地方病平衡點(diǎn);SIVS流行病模型;Lyapunov函數(shù)
流行病的數(shù)學(xué)建模無(wú)論是在流行病管理與控制的理論方面,還是在實(shí)踐方面都非常重要。研究者通過(guò)建立能夠準(zhǔn)確地描述流行病傳播特點(diǎn)的數(shù)學(xué)模型,利用各種數(shù)學(xué)理論,研究流行病的傳播規(guī)律,從而為控制流行病的傳播提供理論依據(jù)。近年來(lái),流行病模型的動(dòng)力學(xué)行為研究已取得豐富的成果。一般地,在一個(gè)流行病模型中,通常會(huì)存在一個(gè)閾值。當(dāng)該閾值小于或等于1時(shí),這類(lèi)模型通常有唯一的無(wú)病平衡點(diǎn),并且該平衡點(diǎn)全局漸近穩(wěn)定;當(dāng)該閾值大于1時(shí),無(wú)病平衡點(diǎn)不穩(wěn)定,此時(shí)系統(tǒng)會(huì)存在另外一個(gè)平衡點(diǎn),即地方病平衡點(diǎn),并且該點(diǎn)也是全局漸近穩(wěn)定的。由此可知,閾值的存在從理論上提供了控制流行病蔓延的預(yù)防措施。
流行病的控制是困難并且復(fù)雜的。 接種疫苗是控制流行病傳播和消除流行病的一種非常重要并且基本的策略, 因此, 越來(lái)越多的學(xué)者開(kāi)始研究帶有接種疫苗的流行病模型[1-3], 并且獲得了豐富的研究成果。 起初研究的最經(jīng)典的SIVS流行病模型并沒(méi)有考慮環(huán)境因素的隨機(jī)干擾, 然而, 生活中處處充滿(mǎn)了環(huán)境因素的隨機(jī)干擾,任何系統(tǒng)都無(wú)法逃避環(huán)境噪聲的影響。 在流行病模型的后續(xù)研究中, 為了盡可能符合實(shí)際情況, 數(shù)學(xué)家和生物學(xué)家都開(kāi)始從事隨機(jī)流行病模型的研究[4-5]。 May[6]得出環(huán)境的隨機(jī)變化將會(huì)導(dǎo)致出生率、 死亡率、 接觸率等參數(shù)的隨機(jī)波動(dòng)的結(jié)論。 受其啟發(fā), Zhao等[7]通過(guò)假定環(huán)境噪聲主要影響接觸率, 研究了相應(yīng)的隨機(jī)SIVS流行病模型。 無(wú)論是經(jīng)典的SIVS流行病模型還是隨機(jī)SIVS流行病模型[7], 均采用了雙線性發(fā)病率。為了使研究更有現(xiàn)實(shí)意義,近年來(lái)研究者提出了各種形式的非線性發(fā)病率模型[8-10]。Zhao等[11]通過(guò)準(zhǔn)確地給定隨機(jī)傳染病模型閾值的表達(dá)式,分析閾值所滿(mǎn)足的條件,著重討論了隨機(jī)系統(tǒng)的絕滅與隨機(jī)持久生存問(wèn)題。
本文中采用不同于文獻(xiàn)[11]中的方法, 通過(guò)構(gòu)造合適的Lyapunov函數(shù), 利用Lyapunov方法分別討論確定性模型與隨機(jī)模型這2類(lèi)系統(tǒng)的穩(wěn)定性。 首先, 研究具有非線性發(fā)病率的確定性SIVS流行病模型; 然后, 在假設(shè)接觸率受到環(huán)境白噪聲的隨機(jī)擾動(dòng)的條件下, 建立相應(yīng)的隨機(jī)SIVS流行病動(dòng)力學(xué)模型, 利用隨機(jī)微分方程的基本理論, 討論隨機(jī)模型的動(dòng)力學(xué)行為。
1 模型概述
基于經(jīng)典的SIR模型建立的SIVS模型[2],即帶有接種疫苗的SIS模型為
(1)
式中:t為時(shí)間;S(t)為易感人群的數(shù)量;I(t)為感染人群的數(shù)量;V(t)為接種疫苗后獲得免疫的人群的數(shù)量;Λ為易感人群中新生者人口的數(shù)量;q為新生者中接種疫苗的比率;β為接觸率;μ為易感者、感染者、免疫者S、I、V的自然死亡率;p為易感者中接種疫苗的比率;γ為感染者的恢復(fù)率;δ為免疫者中失去免疫力回歸易感者的比率;α為因病死亡率。參數(shù)Λ、q、β、μ、p、γ、δ、α均為正常數(shù)。
文獻(xiàn)[7]中假定環(huán)境噪聲影響了接觸率β, 即β→β+σB(t)(其中B(t)為標(biāo)準(zhǔn)的布朗運(yùn)動(dòng),且強(qiáng)度σ2>0),進(jìn)而有如下隨機(jī)SIVS模型[7]:

(2)
可以看出,系統(tǒng)(1)、(2)均采用雙線性發(fā)病率βSI。本文中采用非線性發(fā)病率形式SI/f(I),得到確定性系統(tǒng)
(3)
式中f(I)為連續(xù)、可微函數(shù),f(0)=1,且f′(I)≥0。
引入隨機(jī)擾動(dòng),得到如下隨機(jī)SIVS系統(tǒng):
(4)
式中f(I)為連續(xù)、可微函數(shù),f(0)=1,且f′(I)≥0。
2 確定性系統(tǒng)(3)的動(dòng)力學(xué)行為
令N(t)=S(t)+I(t)+V(t), 可得N′(t)=Λ-μN(yùn)(t)-αI(t)。 顯然,D={(S,I,V)∶S≥0,I≥0,V≥0,S+I+V≤Λ/μ}是系統(tǒng)(3)的正定不變集,因此,僅考慮系統(tǒng)(3)在D中的解。
(5)
由于f(0)=1且f′(I)≥0,因此可得方程(5)的等價(jià)方程為
(6)
把方程(6)中的S(t)、V(t)代入第1個(gè)等式,可得



記

顯然R0可定義為該系統(tǒng)的基本再生數(shù)。參照文獻(xiàn)[2]中的方法來(lái)研究系統(tǒng)(3)的無(wú)病平衡點(diǎn)P0(S0,0,V0)與地方病平衡點(diǎn)P*(S*,I*,V*)的穩(wěn)定性。
定理1 當(dāng)R0≤1時(shí),系統(tǒng)(3)的無(wú)病平衡P0全局漸近穩(wěn)定。
因?yàn)閒(I)滿(mǎn)足f(0)=1且f′(I)≥0, 所以當(dāng)I>0時(shí), 有f(I)≥1恒成立。又由于S≤Λ/μ,因此

[βS-(μ+γ+α)]I≤


(1-q)Λ-(μ+p+δ)S+δN≤





從而

又由于




綜合1)、2),定理1得證。
定理2 當(dāng)R0>0,α2p<4μ(μ+α)(μ+δ)時(shí),系統(tǒng)(3)的地方病平衡點(diǎn)P*全局漸近穩(wěn)定。
證明:由于R0>1,系統(tǒng)(3)存在唯一的地方病平衡點(diǎn)P*(S*,I*,V*),因此


qΛ+pS*=(μ+δ)V*。
記N*=S*+I*+V*,對(duì)系統(tǒng)(3)變形可得
(7)
定義



mV11(I)+nV12(V)+V13(N),
其中m=(2μ+α)/β,n=(2μ+α)/p。
經(jīng)計(jì)算,得


dV12(V)=[p(V-V*)(N-N*)-
p(I-I*)(V-V*)-
(μ+p+δ)(V-V*)2]dt,
dV13(N)=[-μ(N-N*)2-α(I-I*)(N-N*)]dt。
因此,
dV1=mdV11+ndV12+dV13=
{-βm(I-I*)2-(βm+np)(I-I*)(V-V*)+
(βm-α)(I-I*)(N-N*)-

n(μ+p+δ)(V-V*)2+
因?yàn)閒(0)=1且f′(I)≥0,所以[f(I)-f(I*)]·(I-I*)≥0,f(I*)≥1。從而,
dV1≤[-βm(I-I*)2-(βm+np)(I-I*)(V-V*)+
(βm-α)(I-I*)(N-N*)-
n(μ+p+δ)(V-V*)2+
np(V-V*)(N-N*)-μ(N-N*)2]dt=
[-(2μ+α)(I-I*)2-2(2μ+α)(I-I*)(V-V*)+

(2μ+α)(V-V*)(N-N*)-μ(N-N*)2]dt=
{-(2μ+α)[(I-I*)2+(V-V*)2+







{-(2μ+α)[(I-I*)+(V-V*)-




定理2得證。
3 隨機(jī)系統(tǒng)(4)的動(dòng)力學(xué)行為
確定性系統(tǒng)(3)的無(wú)病平衡點(diǎn)P0顯然仍為隨機(jī)系統(tǒng)(4)的無(wú)病平衡點(diǎn),但是系統(tǒng)(3)的地方病平衡點(diǎn)P*不再是隨機(jī)系統(tǒng)(4)的平衡點(diǎn)。本節(jié)中討論隨機(jī)系統(tǒng)(4)的無(wú)病平衡點(diǎn)P0(S0,0,V0)的隨機(jī)穩(wěn)定性,以及隨機(jī)系統(tǒng)(4)的解關(guān)于確定性系統(tǒng)(3)地方病平衡點(diǎn)P*(S*,I*,V*)的漸近行為。
3.1 隨機(jī)微分方程的相關(guān)知識(shí)
設(shè)(Ω,F,{F}t,P)為一個(gè)完備概率空間,其中Ω為一個(gè)非空集合,稱(chēng)為樣本空間,F(xiàn)為樣本空間冪集的一個(gè)非空子集,{F}t為濾子,P為概率或概率測(cè)度。濾子{F}t滿(mǎn)足一般性條件,即遞增,右連續(xù),并且F0包含所有的P零集。

dX(t)=f[X(t),t]dt+g[X(t),t]dB(t),t≥t0,
(8)
式中:f(x,t)為定義在Rd×[t0,+∞)到Rd的函數(shù);g(x,t)為d×m型矩陣,且f和g是關(guān)于x的局部Lipschitz函數(shù);B(t)為定義在上述空間上的m維布朗運(yùn)動(dòng)。
定義1[12]對(duì)于隨機(jī)微分方程(8), 假定解的存在唯一性定理滿(mǎn)足, 對(duì)于任意給定的初值x(t0)=x0∈Rd, 方程(8)有唯一的全局解x(t;t0,x0),如果初值x(t0)=0且
f(0,t)=0,g(0,t)=0,t≥t0,
那么方程(8)有解x(t)=0,這個(gè)解叫做方程的零解或平衡點(diǎn)。
設(shè)C2,1(Rd×[t0,+∞);R+)是定義在Rd×[t0,+∞)上所有正定函數(shù)V(x,t)的集合,則V(x,t)是連續(xù)函數(shù),且關(guān)于x二階可導(dǎo),關(guān)于t一階可導(dǎo)。引入一個(gè)關(guān)于微分方程(8)的微分算子


如果L作用函數(shù)V(x,t)∈C2,1(Rd×[t0,+∞);R+),那么
LV(x,t)=Vt(x,t)+Vx(x,t)f(x,t)+
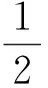
定義2[12]1)如果對(duì)任意的ε∈(0,1)和r>1,存在δ=δ(ε,r,t0)>0,使得當(dāng)|x0|<δ時(shí),隨機(jī)微分方程(8)的解x(t;t0,x0)滿(mǎn)足
P{|x(t;t0,x0)| 則稱(chēng)方程(8)的零解隨機(jī)穩(wěn)定(或依概率穩(wěn)定)。否則,稱(chēng)方程(8)的零解隨機(jī)不穩(wěn)定。 2)如果方程(8)的零解隨機(jī)穩(wěn)定,且對(duì)于任意給定的ε∈(0,1),存在δ0=δ0(ε,t0)>0,使得當(dāng)|x0|<δ0時(shí),有 則稱(chēng)方程(8)的零解隨機(jī)漸近穩(wěn)定。 3)如果方程(8)的零解隨機(jī)漸近穩(wěn)定,且對(duì)于任意的x0∈Rd,有 則稱(chēng)方程(8)的零解全局隨機(jī)漸近穩(wěn)定。 引理1[12]如果存在正定的徑向無(wú)界函數(shù)V(x,t)∈C2,1(Rd×[t0,+∞);R+)使得LV(x,t)是負(fù)定的,則隨機(jī)微分方程(8)的零解全局隨機(jī)漸近穩(wěn)定。 顯然D={(S,I,V)∶S≥0,I≥0,V≥0,S+I+V≤Λ/μ} 仍然是系統(tǒng)(4)的正定不變集,因此,以下仍在D中討論隨機(jī)系統(tǒng)(4)的解。 證明:顯然P0(S0,0,V0)是系統(tǒng)(4)的無(wú)病平衡點(diǎn),因此 (1-q)Λ=(μ+p)S0-δV0, qΛ=(μ+δ)V0-pS0。 令x=S-S0,y=I,z=V-V0,則有 (9) 定義 c1V21(y)+c2V22(x,y)+V23(x,y,z), 運(yùn)用伊藤公式[12],可得 dV2(x,y,z)=c1dV21(y)+c2dV22(x,y)+dV23(x,y,z)= [c1LV21(y)+c2LV22(x,y)+ 具體地, dV22(x,y)=(x+y)[-(μ+p)x-(μ+α)y+δz]dt= [-(μ+p)x2-(2μ+p+α)xy+δxz- (μ+α)y2+δyz]dt=LV22dt, dV23(x,y,z)=(x+y+z)[-μx-(μ+α)y-μz]dt= [-μx2-(2μ+α)xy-2μxz-(μ+α)y2- (2μ+α)yz-μz2]dt=LV23dt。 由于f(0)=1,f′(I)≥0,因此f(y)=f(I)≥1。 又R0≤1,因此 [β(x+S0)-(μ+γ+α)]y= βxy+[βS0-(μ+γ+α)]y≤βxy, 從而 LV2=c1LV21+c2LV22+LV23≤-[μ+c2(μ+p)]x2+ [c1β-c2(2μ+p+α)-(2μ+α)]xy+ (c2δ-2μ)xz-[(1+c2)(μ+α)]y2+ [c2δ-(2μ+α)]yz-μz2。 所以 c1β-c2(2μ+p+α)-(2μ+α)=0, c2δ-2μ=0。 從而 上述過(guò)程中應(yīng)用了對(duì)于任意實(shí)數(shù)a、b,有(a+b)2≥0即-2ab≤a2+b2恒成立這一性質(zhì)。 因此,LV2≤0。由引理1可知,P0全局隨機(jī)漸近穩(wěn)定。 定理3得證。 假定R0>1,研究隨機(jī)系統(tǒng)(4)的解在確定性系統(tǒng)(3)的地方病平衡點(diǎn)P*附近的漸近行為。 時(shí),有 (μ-ρα)[V(r)-V*]2}dr≤ 證明:由于R0>1,系統(tǒng)(3)有唯一的正平衡點(diǎn)即地方病平衡點(diǎn)P*,因此 qΛ+pS*=(μ+δ)V*。 定義 c1V31(I)+c2V32(S,I)+V33(S,I,V), 運(yùn)用伊藤公式[12],可得 dV3(S,I,V)=c1dV31(I)+c2dV32(S,I)+dV33(S,I,V)= [c1LV31(I)+c2LV32(S,I)+ 具體地, dV32(S,I)=[(S-S*)+(I-I*)][-(μ+p)· (S-S*)-(μ+α)(I-I*)+ δ(V-V*)]dt=[-(μ+p)(S-S*)2- (2μ+p+α)(S-S*)(I-I*)+δ(S- S*)(V-V*)-(μ+α)(I-I*)2+ δ(I-I*)(V-V*)]dt=LV32dt, dV33(S,I,V)=[(S-S*)+(I-I*)+(V-V*]· [-μ(S-S*)-(μ+α)(I-I*)- μ(V-V*)]dt[-μ(S-S*)2- (μ+α)(I-I*)2-μ(V-V*)2- (2μ+α)(S-S*)(I-I*)- 2μ(S-S*)(V-V*)-(2μ+α)· (I-I*)(V-V*)]dt=LV33dt。 從而 由此可知, LV3=c1LV31+c2LV32+LV33≤ -[μ+c2(μ+p)](S-S*)2-(1+c2)· (μ+α)(I-I*)2-μ(V-V*)2+ [c1β-c2(2μ+p+α)-(2μ+α)](S-S*)· (I-I*)+(c2δ-2μ)(S-S*)(V-V*)+ c1β-c2(2μ+p+α)-(2μ+α)=0, c2δ-2μ=0。 從而 同樣,上述過(guò)程中應(yīng)用了對(duì)于任意實(shí)數(shù)a、b有(a+b)2≥0即-2ab≤a2+b2恒成立這一性質(zhì)。 因此 不等式兩邊同時(shí)從0到t求積分,則 V3(t)-V3(0)≤ 因此 (μ-ρα)(V(r)-V*)2}dr≤V3(0)+ 令 是一個(gè)實(shí)值局部鞅,且M(0)=0。顯然, (μ-ρα)(V(r)-V*)2}dr≤ 幾乎處處成立。 定理4得證。 本文中通過(guò)討論確定性模型、隨機(jī)模型2類(lèi)具有非線性發(fā)病率SI/f(I)的SIVS流行病模型,得到如下主要結(jié)論: 1)在確定性模型中,系統(tǒng)存在基本再生數(shù);當(dāng)基本再生數(shù)小于或等于1時(shí),系統(tǒng)只有唯一的平衡點(diǎn),即無(wú)病平衡點(diǎn),并且該平衡點(diǎn)全局漸近穩(wěn)定,疾病最終滅絕;當(dāng)基本再生數(shù)大于1時(shí),無(wú)病平衡點(diǎn)不再穩(wěn)定,系統(tǒng)存在唯一的地方病平衡點(diǎn),并且得到全局漸近穩(wěn)定的充分條件,即只有在一定條件下,地方病平衡點(diǎn)才全局漸近穩(wěn)定,疾病才會(huì)盛行。 2)在隨機(jī)模型中,當(dāng)確定性系統(tǒng)的基本再生數(shù)小于或等于1時(shí),該系統(tǒng)的無(wú)病平衡點(diǎn)與確定性系統(tǒng)相同,因此在因病死亡率滿(mǎn)足一定條件的情況下,該平衡點(diǎn)全局隨機(jī)漸近穩(wěn)定。這表明引入隨機(jī)擾動(dòng)后,可以通過(guò)控制因病死亡率來(lái)控制疾病,進(jìn)而使疾病絕滅;當(dāng)基本再生數(shù)大于1時(shí),確定性系統(tǒng)的地方病平衡點(diǎn)已不是隨機(jī)系統(tǒng)的平衡點(diǎn),此時(shí),隨機(jī)系統(tǒng)的解在相應(yīng)確定性系統(tǒng)的地方病平衡點(diǎn)附近波動(dòng),并且波動(dòng)強(qiáng)度與擾動(dòng)強(qiáng)度成正比,因此,可以通過(guò)控制擾動(dòng)強(qiáng)度來(lái)控制疾病。 [1] LI J Q, MA Z E. Qualitative analyses of SIS epidemic model with vaccination and varying total population size[J]. Math Comput Model, 2002, 35(11/12): 1235-1243. [2] LI J Q, MA Z E. Global analysis of SIS epidemic models with variable total population size[J]. Math Comput Model, 2004, 39(11): 1231-1242. [3] MONEIM I A, GREENHALGH D. Threshold and stability results for an SIRS epidemic model with a general periodic vaccination strategy[J]. J Biol Syst, 2011, 13(2): 131-150. [4] LAHROUZ A, OMARI L. Extinction and stationary distribution of a stochastic SIRS epidemic model with non-linear incidence[J]. Statist Probab Lett, 2013, 83(4): 960-968. [5] WITBOOI P J. Stability of an SEIR epidemic model with independent stochastic perturbations[J]. Physica: A, 2013, 392(20): 4928-4936. [6] MAY R M. Stability and complexity in model ecosystems[M]. Princeton: Princeton University Press, 2001. [7] ZHAO Y N, JIANG D Q, REGAN D O. The extinction and persistence of the stochastic SIS epidemic model with vaccination[J]. Physica: A, 2013, 392(20): 4916-4927. [8] CAPASSO V, SERIO G. A generalization of the Kermack-Mckendrick deterministic epidemic model[J]. Math Biosci, 1978, 42(1/2): 43-61. [9] XIAO D, RUAN S. Global analysis of an epidemic model with a nonmonotone incidence rate[J]. Math Biosci, 2007, 208(2):419-429. [10] LAHROUZ A, OMARI L, KIOUACH D, et al. Complete global stability for an SIRS epidemic model with generalized non-linear incidence and vaccination[J]. Appl Math Comput, 2012, 218(11): 6519-6525. [11] ZHAO D L, ZHANG T S, YUAN S L. The threshold of a stochastic SIVS epidemic model with nonlinear saturated incidence[J]. Physica: A, 2016, 443: 372-379. [12] MAO X R. Stochastic differential equations and applications[M]. Chichester: Horwood, 1997. DynamicBehaviorofSIVSEpidemicModelswithNonlinearIncidenceRate QUMeifeng,DONGLingzhen (College of Mathematics, Taiyuan University of Technology, Taiyuan 030024, China) nonlinear incidence rate; disease-free equilibrium; endemic equilibrium; SIVS epidemic model; Lyapunov function 2017-03-30 < class="emphasis_bold">網(wǎng)絡(luò)出版時(shí)間 時(shí)間:2017-12-13 16:49 教育部科學(xué)技術(shù)研究重點(diǎn)項(xiàng)目(210030);山西省自然科學(xué)基金項(xiàng)目(2013011002-3) 曲美鋒(1991—),女,山西忻州人。碩士研究生,研究方向?yàn)槲⒎址匠汤碚撗芯考捌鋺?yīng)用。E-mail:1220533082@qq.com。 董玲珍(1970—),女,山西太原人。教授,博士,研究方向?yàn)槲⒎址匠汤碚撗芯考捌鋺?yīng)用。E-mail:linzhen_dong@aliyun.com。 http://kns.cnki.net/kcms/detail/37.1378.N.20171212.1637.018.html 1671-3559(2018)01-0060-10 10.13349/j.cnki.jdxbn.2018.01.009 O175.13;O211.63 A (責(zé)任編輯:王耘)

3.2 無(wú)病平衡點(diǎn)的穩(wěn)定性


















3.3 解的漸近行為





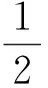
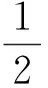










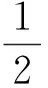






















4 結(jié)論


