數學解題中對化歸思想的運用
◎張雯倩
數學解題中對化歸思想的運用
◎張雯倩
數學學習是為了將理論知識和思維方式使用在實際中,這是高中學習階段中十分關鍵的一門學科。我們在對其進行學習的時候,需要將相關的知識點有效地運用在解題中,這樣才達到了學習的真正目的。化歸思想是我們進行數學解題時常用的一種思想,其能夠讓復雜的問題變得簡單化。本文就在實際例題的基礎上,詳細地闡述化歸思想在數學解題中的實際運用。
和初中數學相比,高中數學涵蓋范圍更廣,其知識更加深入。我們在學習時總是感到其存在一定的難度,對有些概念知識無法進行全面的掌握,這樣就讓我們進行解題時存在阻礙。而將化歸思想使用在數學解題中,能夠讓題目更加簡單,進而提升我們的解題效率。
化歸思想在數學解題中的作用
在化歸思想中的化就是變化原問題,轉化原問題;而歸則是變化、變換原問題。這是一種在高中數學解題中常用的方式。從具體的情況來看,化歸思想能夠把復雜的問題進行有效的變換轉化,使其成為更加簡單的問題;把難度高的問題經過變換轉化成容易問題;把未能夠解決的問題經過變換轉化為已解決的問題。在這其中也可以是形式上的轉換。例如命題之間的轉化、數與形的轉化、空間向平面的轉化以及多元向一元轉化等等,這些都是轉化思想具體體現。我們在學習數學的時候,要將相關的知識和解題方式合理的使用在解題過程中,在解題中將化歸思想溶入進去,進而掌握更多的學習與解題技巧。在對數學題進行解答的時候,我們經常會遇到一些直接求解困難的問題,經過觀察、分析以及聯想等相關的思維過程,或者依據已存在的學習經驗,選用合理的方法進行變換,把原來問題轉化成新問題。經過對新問題求解,進行實現解決原問題的目的,這種思想方式是化歸與轉化思想的核心。在不斷的學習與練習過程中,我們可加強對化歸思想的運用,使其融入到解題思路中,進而有效的提升自己的解題效率。
化歸思想在數學解題中的具體運用
在常量問題中的運用
在對高中數學進行學習的時候,我們已經習慣與把x當做任何方程式中的變量,這是一種固定性的思維。但是在某些問題中,將x當做變量的思維會讓解題過程遇到阻礙。所以我們要在數學解題中靈活的運用化歸思想,把式子中的變量當做常量,把常量作為變量,以此開闊自己的解題思路。就常量和變量進行轉化的問題,將下面這道問題作為例子:
例題1:目前已知實數p滿足|p|≤2,其中包含有p的不等式x2+px+1>2x+p恒成立,求出x取值范圍。
解析:我們在解答這道題目的時候,極易將題目認為含有變量x和常量p的不等式求解,若是使用這種思想進行解題,則就會存在很大的難度。若是使用化歸思想,把式子中的x作為常量,把p當做變量,則就能夠讓問題更加簡單。其具體過程是把原式子化為有關p的一元一次不等式p(x-1)+(x-1)2>0,然后得出f(p)=p(x-1)+(x-1)2。這樣就能夠把原式子轉換成為一元一次不等式,之后解答出x<1。經過對這個例題的解答,我們就能夠知道把常量問題轉換成為變量能夠更加輕松地解題。
在幾何問題中的運用
將化歸思想使用在幾何相關的問題中,使用分割、變形以及展開等相關方式,繪制輔助線對空間平面圖形進行處理,進而把立體問題化歸于平面問題,這是我們在解答立體幾何問題時常使用的方式。
例題2:就圖1所示,正三棱錐P-ABC中,各個棱商都是2,其中E為側棱PC的重點。現在有一只螞蟻在A點出發,經過側面PAB與側面PBC到E點,試著求出螞蟻走過的最短距離。
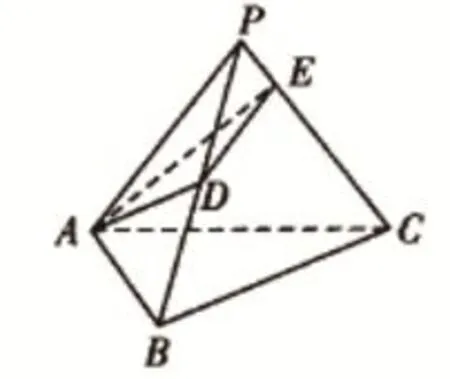
圖1
解析:在解答這個問題的時候,我們都知道平面上兩個點距離最短。在對三棱錐中兩個點最短距離進行求解時,可以將圖形展開,這是將立體幾何化作平面問題的基礎,經過展開之后如圖2。
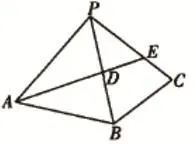
圖2
經由平面中兩點距離最短可知,其中最短距離是線段AE,在三角性PAE中,PA=2,PE=1,且∠APE=,由余弦定理獲得AE=。通過這個問題的解答我們就能夠知道將立體圖展開,其實際上能夠讓空間圖形中一些不容易發現的幾何體出現,將相關的元素位置關系與數量關系呈現出來。
在函數問題中的運用
函數是高中數學知識中關鍵的構成部分,將化歸思想使用在函數解題中能夠衍生出幾種方式。其一,函數中動和靜的轉化,使用化歸思想把處在靜態的量構成動態的函數形式,依據函數運動特點對實際例題進行解答。
解析:我們在解答這道題目的時候,就能夠使用函數中動靜相互轉換的形式進行解答,將這兩個數量的函數進行構建,經過對比函數圖象的模式,最后得出這個結果。還有則是函數中數與形以及轉換成為根的解題方式,這些都是將化歸思想使用在函數中的常用方式。
數學的學習能夠有利于我們思維邏輯的培養,將相關的理論知識使用在解題過程中能夠提高自己運用知識的能力。作為數學解題中常用的一種思想方式,化歸思想能夠有效的簡化數學難題,開拓我們的的解題思路,進而正確有效的解答題目,提升自己數學學習能力。
長沙市麓山國際實驗學校)

