斯特林循環效率的實驗模擬與理論分析

魏志遠 聶 婭 向 鋼

(四川大學物理科學與技術學院，四川 成都 610064)

斯特林循環效率的實驗模擬與理論分析

魏志遠 聶 婭 向 鋼

(四川大學物理科學與技術學院，四川 成都 610064)

本文從實驗上驗證了斯特林循環的效率與卡諾循環的效率一致。實驗結果和理論分析表明，工作物質在等體過程中吸收的熱量無須計入循環效率的計算公式，因為斯特林循環中的回熱器是在系統內部與工作物質進行熱量的交換，對外界沒有影響。

斯特林循環；卡諾循環；循環效率

熱學課程的基本內容之一是熱機及與其相關的理論。我們的日常生產和生活都離不開能源的供給，而人類目前的能源供給主要來自于化石燃料。化石燃料的燃燒可產生熱，將熱轉化為機械能的裝置即是熱機。利用熱力學第一定律，我們可以分析熱機的循環過程中的功熱轉換，計算不同類型熱機的工作效率。本文將結合實驗結果與理論分析討論一種高效率的循環過程——斯特林循環。

熱機的研制是18世紀物理學和工程學的中心課題。當時，各種各樣的熱機被發明改良，并且相互借鑒、取長補短，極大地提高了生產效率，工業革命處于蓬勃發展的高速時期。隨著熱機的發展，相關理論的研究排到了極其重要的位置，一大批科學家致力于熱機理論的研究工作，英國物理學家斯特林(R.Stirling，1790—1878)便是其中一位著名的人物。1816年，他提出斯特林循環，亦稱“斯特林熱氣機循環”，這是一種封閉式的定體條件下吸熱的氣體循環方式。利用這種循環工作的“斯特林熱機”具有獨特的優點：采用外熱源供熱，不會像內燃機那樣容易發生爆震；封閉式的循環能夠利用遠高于大氣壓的高壓氣體工作，由此可以提高發動機單位重量的功率，減小發動機的體積和重量。而且，此類循環的理論效率具有熱機的理論最大效率，即和在相同的高溫熱源和低溫熱源間工作的卡諾循環的效率相等。由于斯特林循環的獨特性和高效性，斯特林熱機已在航天、陸上、水下等領域得到了廣泛的應用[1]。

由于斯特林循環較之其他循環的優勢性，對它的理論探索工作一直都沒有停止過[2,3]，但國內外文獻，包括教材，對實驗驗證方面的工作介紹卻極為罕見。在本文中，我們利用斯特林熱機的模型機——空氣熱機，通過搭建的實驗裝置，分別對兩臺熱機的工作效率進行了實驗測定，結果顯示，斯特林熱機的工作效率與卡諾熱機的工作效率相等，并由此從實驗上驗證了工作物質與回熱器在等體過程中交換的熱量無需計入效率的理論計算公式。

1 斯特林循環的工作效率及斯特林熱機的工作原理

1.1 斯特林循環的工作效率的理論分析

圖1所示為斯特林循環的過程曲線：a→b為等溫壓縮過程，b→c為等體升溫過程，c→d為等溫膨脹過程，d→a為等體降溫過程。其中，工作物質在b→c的等體升溫過程和c→d的等溫膨脹過程中有吸熱，分別為

(1)

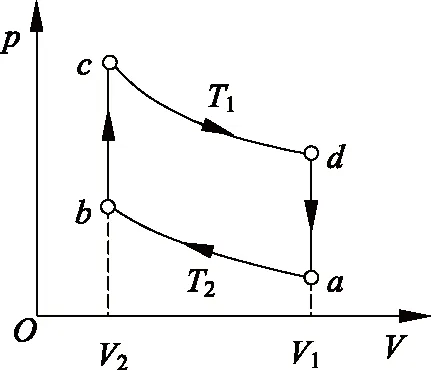
圖1 正向斯特林循環

式中,ν為工作物質的摩爾數;T1>T2。在d→a的等體降溫過程和a→b的等溫壓縮過程中有放熱，分別為

(2)

在一個循環過程中，工作物質對外做的凈功為

(3)

工作物質吸收的總熱量為

(4)

于是，由熱機的循環效率的基本公式[4]，可得

(5)

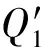
但是實際上斯特林循環的效率[3]應為

(6)

即在計算熱機效率時，不必考慮兩個等體過程中工作物質吸收和釋放的熱量。這是因為，斯特林在熱機中設計了一個回熱器，工作物質的等體吸熱和等體放熱都是在系統的回熱器內部進行，不對外界產生任何影響[3]。由于工作物質只在兩個等溫過程中才與外界交換熱量，故在斯特林循環的效率計算公式中，不計入等體升溫過程中工作物質吸收的熱量。這就使得理想的斯特林循環具有和卡諾循環相同的工作效率，而成為高效的熱機循環。

在一些國外的教材[5]中，斯特林循環的工作效率仍然采用式(5)，即把工作物質吸收的所有的熱量都考慮在內。兩種關于斯特林循環效率的定義，究竟哪一種更符合實際呢？下面我們將通過實驗來進行驗證分析。

1.2 斯特林熱機的工作原理

斯特林熱機的結構有多種類型，包括自由活塞式、配氣活塞式和四缸雙作用式3種基礎結構，以及它們的變形。下面介紹配氣活塞式熱機的工作原理，如圖2所示。

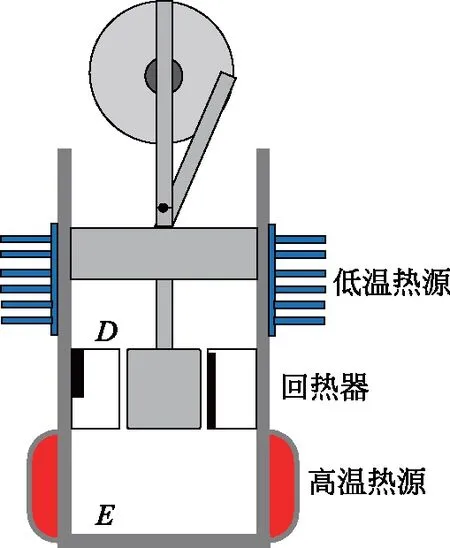
圖2 配氣活塞式斯特林發動機

氣缸內部充滿了氣體(即工作物質)。上面的活塞稱為“動力活塞”，其上移使得工作物質“膨脹”，下移使得工作物質被“壓縮”；下面的活塞稱為“配氣活塞”，其上移使得工作物質被“加熱”，下移使得工作物質“冷卻”。

通過曲軸排布，使得配氣活塞領先動力活塞1/4周期，結合圖1，有：

(1) 等溫壓縮過程(a→b)：動力活塞下行，氣體被等溫壓縮，熱量在T2溫度下由氣體釋放給低溫熱源(如冷凝器)；

(2) 等體升溫過程(b→c)：配氣活塞上行，D中部分氣體流向E，當氣體通過回熱器時，則從回熱器吸熱，溫度升高為T1。由于動力活塞不動，故過程是等體的；

(3) 等溫膨脹過程(c→d)：配氣活塞和動力活塞同時上行，氣體等溫膨脹，熱量在T1溫度下從高溫熱源流向氣體；

(4) 等體降溫過程(d→a)：配氣活塞下行至它初始的位置，E中部分氣體流向D，當氣體通過回熱器時，則向回熱器放熱，溫度降低為T2。由于動力活塞不動，故過程是等體的。

2 斯特林循環效率的實驗模擬及數據分析

測量斯特林循環工作效率的實驗裝置如圖3所示，主要裝置包括：電加熱空氣熱機實驗儀、通信器和雙蹤示波器，以及空氣熱機測試儀和電加熱電源等。其中，空氣熱機的工作原理與配氣活塞式斯特林熱機類似[6]，其最大不同是將動力活塞(即工作活塞)與配氣活塞(即位移活塞)的工作區域做了物理分割：工作活塞處于工作汽缸，位移活塞處于位移氣缸內，如圖4所示。

圖3 實驗裝置

我們利用搭建的實驗裝置來測量斯特林熱機的工作效率，并由此來驗證卡諾定理。高溫熱源與低溫熱源的溫度從空氣熱機測試儀讀取，輸出的機械功從p-V圖圍成的面積讀取(此實驗采用信號轉換器將實時數據輸入到電腦中，再由專用軟件處理，可以直接讀取該面積所代表的機械功的大小)。

實驗中，在加熱器的作用下，位移氣缸熱端的溫度T1會隨時間逐漸增加，溫度越高，其輸出功率越大，于是轉速n會隨之增大。

我們選取了兩臺相同型號的空氣熱機實驗儀，Ⅰ和Ⅱ。第一次實驗，在儀器Ⅰ上進行，由于實驗條件限制，只能將高溫熱源溫度(加熱電壓)調節到幾個設定的值，將相關數據記錄在表1中。

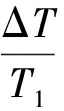
由圖5可以看到，實驗數據ΔT/T1與nW/ΔT成一定的線性關系，線性相關度為r=0.94653。

圖 4 (a) 空氣熱機示意圖； (b) 實驗儀的低溫熱源； (c) 高溫熱源； (d) 位移活塞

高溫熱源溫度T1/℃低溫熱源溫度T2/℃轉速n/(2π·rad·s-1)溫差ΔT/℃輸出功W/JΔTT1nWΔT454．1309．85．3144．30．15560．3177714160．005715038454．6309．75．1144．90．15640．3187417510．005504762494．7313．771810．16710．365878310．006462431495．1314．16．91810．16740．3655827110．006381547495．2314．16．9181．10．16720．3657108240．006370403520．8317．98202．90．17230．3895929340．006793494521318．18．2202．90．17140．3894433780．006926959535．5321．610213．90．16820．3994397760．007863488536．2321．610．3214．60．1670．4002237970．008015377536．6321．810．2214．80．16820．4002981740．007987151

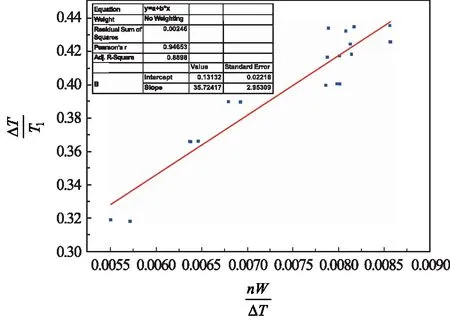
圖5 由第一次測量數據繪制的實驗曲線

圖6 由第二次測量數據繪制的實驗曲線

從圖6可以看出，由測量的實驗數據ΔT/T1與nW/ΔT所繪制出的數據點均分布在擬合直線附近，而且線性相關度達到r=0.98049，表明數據間呈很高的線性關系，ΔT/T1∝nW/ΔT，卡諾定理得到驗證。同時這也說明斯特林熱機的循環效率與卡諾熱機的循環效率相等，即ηS=ηC。

實驗結果同時表明在斯特林循環中，工作物質在等體過程中的吸、放熱的確是在系統內部完成的，對外界沒有任何影響，所以工作物質在等體過程中吸收的熱量不帶入效率的計算公式。當然，這也說明，斯特林設計的回熱器是一個非常絕妙的設想，從而使得斯特林循環能夠具有最高的理論循環效率。根據循環過程求循環效率是每一個學習熱學課程的學生都會經歷的基本訓練，但是熱機是一個工程問題，對于有獨特設計的熱機而言，普遍的熱機效率的計算公式不能生搬硬套，這個經驗對于熱學課程以及其他大學物理課程的教學而言是頗具啟發性的。

3 結論

通過實驗驗證了斯特林循環的效率與卡諾循環的效率是一致的。我們的實驗結果和理論分析表明，計算斯特林熱機效率時，工作物質在兩個等體過程中吸、放熱不必計入效率的計算公式，即在計算循環效率時，我們付出的“代價”只考慮工作物質在等溫膨脹過程中從高溫熱源吸收的熱量，這是符合實驗事實的正確選擇。

[1] 金東寒．斯特林發動機技術[M]．哈爾濱:哈爾濱工程大學出版社，2009．

[2] 張志國，G. David．一維斯特林發動機的數值模型[J]．華中科技大學學報，2006，34(3)：71-74．

Zhang Zhiguo, G. David. 1D numerical model ofStirling engine[J]. J. Huazhong Univ. of sci. & tech. (Nature science edition), 2006, 34(3): 71-74. (in Chinese)

[3] 周雨青．理想斯特林熱機循環原理及其效率的計算和實際工作效率的簡單討論[J]．物理與工程，2015，25(1)：49-52．

Zhou Yuqing. A discussion about the ideal stirling cycle’s principle of operation and factors that influence the efficiency of a real stirling cycle[J]. Physics and Engineering, 2015, 25(1): 49-52. (in Chinese)

[4] 李椿等．熱學[M]．北京：高等教育出版社，2015．

[5] Nolting W． Grundkurs Theoretische Physik 4[M]． German： Springer， 2001．

[6] 王植恒，何原，朱俊,等．大學物理實驗[M]．北京：高等教育出版社，2008．

EXPERIMENTALSIMULATIONANDTHEORETICANALYSISOFTHEEFFICIENCYOFSTIRLINGCYCLE

WEIZhiyuanNIEYaXIANGGang

(College of Physical Science and Technology, Sichuan University, Chengdu Sichuan 610064)

In this paper, we experimentally verified that the efficiency of Stirling cycle is equal to the efficiency of Carnot cycle. The result shows that the heat transformation in the isochoric processes need not be considered in the efficiency formula, because the heat transformation of heat regenerator is inside the Stirling engine, which has no influence on the surroundings outside.

Stirling cycle; Carnot cycle; efficiency

2016-11-30；

2017-08-31

魏志遠，男，2015級教育部物理學試驗班學生，idealbroad@foxmail.com。

聶婭,女，副教授，主要從事大學物理教學工作，研究方向為光學和凝聚態物理，nieya1104@scu.edu.cn。

魏志遠,聶婭,向鋼. 斯特林循環效率的實驗模擬與理論分析[J]. 物理與工程，2017，27(6)：62-65,70.

■