為什么時空變換必須是線性的
陳奎孚
(中國農業大學理學院74#,北京 100083)
為什么時空變換必須是線性的
陳奎孚
(中國農業大學理學院74#,北京 100083)
盡管線性時空變換是狹義相對論的出發點,但至少從教學角度,對線性變換合理性的論證依然不清晰。筆者根據時空均勻性、時空各向同性和慣性系的等價性,嚴格地導出了時空的線性變換,其中關鍵概念是變換的時間縮放系數和空間縮放系數。沿此思路,進一步約束兩個坐標系之間的時空縮放系數相等,并利用光速不變原理,導出了洛倫茲變換。
狹義相對論;洛倫茲變換;光速不變原理;慣性坐標系;慣性定律;勻速直線運動
很多教材在編寫狹義相對論的洛倫茲變換這部分內容時,時空變換被默認成線性了。至于時空變換為什么必須是線性的,大多為泛泛論證。比如,有些教材說同一事件“在兩個參考系中觀察的結果必須是一一對應,這就要求變換關系呈線性”,然而(x′=x3,t′=t)也可以保證一一對應,但它顯然不是線性的。愛因斯坦在最初那篇著名的狹義相對論論文是這樣敘述的,“In the first place it is clear that the equations must belinearon account of the properties of homogeneity which we attribute to space and time”[1](原作為德文,本句英文來自GB Jeffery和W Perrett的1923年英文翻譯版,中文翻譯參見文獻[2]),那愛因斯坦這句敘述是否又靠譜呢?
從另外一個角度,推演狹義相對論的洛倫茲變換究竟需要多少個假設呢?這個問題被很多人討論過了[3],但至少從教學角度,分歧或模糊依然存在[4]。此外,狹義相對論適用于慣性系,但目前推導洛倫茲變換時,表面上并沒有明確使用慣性系的性質。所謂的“在所有慣性系中,物理規律的表達形式都相同”的要求在哪個環節被使用了呢?本文的探究將表明上述問題的解答或多或少與時空變換的線性特性有關。
時空線性變換似乎是狹義相對論的“默認”,而前者被視為近代物理學的兩大支柱之一(另一支柱是量子力學)[5],自然有科學家會審視支柱中“默認”的合理性。Lévy-Leblond曾經討論過這個問題,但沒有說清楚慣性系的貢獻[6]。國內的馮勝奇也討論過同一問題,但出發點與本文不同,結論自然也不同[7]。
“搜盡奇峰打草稿”是清代畫家石濤在書畫創作中極力主張的一種創作觀點。他的書畫作品之所以能有大成,也是因為他身體力行地推崇這句至理名言,所以才能把創作中的意境與靈感淋漓盡致地展現于他的作品當中。對于藝術他主張應該多搜集素材,多觀察事物,手摹心記,在大自然當中不斷地提煉自己的藝術表現手法,總結藝術規律,進而形成自己的藝術風格。以“搜盡奇峰”不辭辛勞的寫生創作態度,從而在“打草稿”的過程中逐漸提煉自己的藝術語言,最終達到“外師造化,中得心源”的至高境界,也是石濤游歷大江南北在奇峰怪石中“山川與予神遇而跡化”的悟道。由此,我對山水畫的寫生創作觀有了“游之、記之、悟之、寫之”的創作感悟。
蔣海峰走向涼臺,異常鎮靜,凝望著深邃的夜空,從來沒有這樣美。他似乎聽到了上帝的召喚,爬上欄桿,輕輕一躍,結束了一切恩怨,結束了苦痛的一生。
在式(14)中,與x相比,時間t并無特殊之處,所以我們也可讓從S到S′的時間縮放系數與從S′到S的相同,即
1 線性時空變換的證明
式(8)代入式(7),并整理可得

圖 1
圖1中P(或稱事件)在S中的坐標為(x,t), 在S′中的坐標為(x′,t′)。兩個坐標系所看到的是同一個事件,所以必然有如下的函數關系
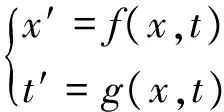
(1a)
(1b)
當然式(1)也必須是可逆的,以保證一一對應。
1.1 時空均勻和各向同性的要求
對式(1)取微分有

(2a)
(2b)

(3)
容易求得偏微分方程(3)的解為
(4)
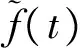
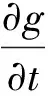
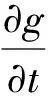
(5)
容易求得偏微分方程(5)的解為
(6)
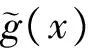
注意式(2)的dx可以沿x軸的正向,也可以沿x軸負向,即式(3)和式(4)的成立要求空間沿x軸兩個方向是同性的(對于空間問題,則進一步要求沿y和z同性;不僅如此, 沿x,y和z三軸任意組合的方向也是同性,即要求空間是各向同性的)。同樣式(2)和式(5)要求時間沿正向和沿反向也是同性的。
綜上,式(2)到式(6)成立的前提為時空是均勻且各向同性。均勻指的是參數不隨時空點而變化,而各向同性指的是有方向的物理量,在不同方向上也是相等的。
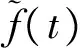
1.2 慣性定律的要求
在外人眼里,老伴是個賢妻良母,在我看來,老伴仍然是個良母,可不是一個賢妻。年輕的時候,我們是同學,走到一起順理成章,感情基礎非常好。后來,有了孩子,生活的瑣碎也沒有影響我們的感情,小日子越過越滋潤。沒想到,到了晚年,因為忙碌小孫子的事,我們少了交流,遇到事情就會爭吵,而且越吵越遠。
x′=k1+k2t′
(7)
其中k1和k2是與x′,t′無關的常數(k1相當于初位置;k2相當于速度)。此時式(1)退變為
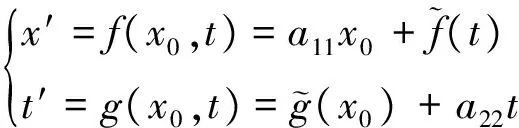
(8a)
(8b)
考慮兩個平移的慣性坐標系S和S′,其中S′的坐標原點相對于S的速度為。因為垂直于的兩個坐標的各自變換是平凡解,為簡潔計,我們的焦點集中于沿相對速度的坐標x和時間t這兩個量的變換關系,如圖1所示。
或可進一步寫為
(9)
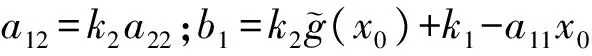
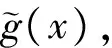
x′=k3+k4t′
(10)
其中k3和k4是與x′,t′無關的常數。此時式(1)退變為
工程法律風險是產生于項目實施過程中,由于行為人的具體行為不規范而導致的,與企業或項目預期目標相違背的法律不利后果發生的可能性。法律風險發生于工程運作過程中,法律風險控制是工程項目管理的重要手段,是全面風險管理的重要支撐。加強工程法律風險管理具有重要的現實意義和經濟效益,是油田企業工程項目的內在要求,是企業適應內外部環境變化的必然選擇,是提升管理水平、實現跨越式發展的迫切需要。
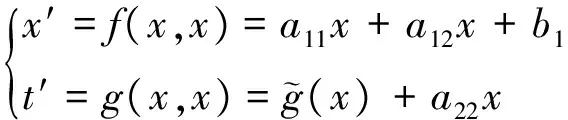
(11a)
(11b)
式(11)代入式(10)整理得到
(12)

將式(9)和式(12)分別代入式(4)和式(6), 就有如下的線性變換
(13)
這即證明了時空變換的線性性質。在這個性質證明中,時空均勻性、時空各向同性和慣性坐標系的等價性等三性缺一不可。
(3)CA-074預處理組(CA-074+LPS組):腹腔注射組織蛋白酶B抑制劑CA-074 10 mg/kg,30 min后腹腔注射致死劑量LPS。
不失一般性,我們可把式(13)進一步限制為標準型,即(x′,t′)=(0,0)與(x,t)=(0,0)對應,這就有b1=0,b2=0。隨后只討論如下的標準型,
(14)
如果放棄時空均勻性和各向同性,只要求慣性系的等價性,自然就不能從式(4)和(6)出發了。讀者可參考文獻[8]對此情形的處理。
2 洛倫茲變換的推導
2.1 對伽利略變換縮放系數的拓展
在牛頓時空下有伽利略變換x′=x-vt,t=t′,它的縮放系數滿足
第三,加強教師專業指導,保障集體實踐活動的有效開展。 集體實踐活動雖然應該充分尊重學生的主體地位,更多地鼓勵學生積極參與。 但是在實踐過程中,學生難免會遇到各種無法解決的問題,這就需要來自教師的專業指導。 學校應選派工作經驗豐富、理論功底深厚的教師參與實踐活動。 專業指導教師一方面應積極參與實踐活動的策劃和審定環節,把握實踐活動的方向性、科學性和可行性,保障集體實踐活動的有效開展; 另一方面在活動的開展過程中,教師也應做到積極參與,引導大學生群體在實踐過程中體悟和踐行集體主義原則,保障實踐活動教育功能的發揮。
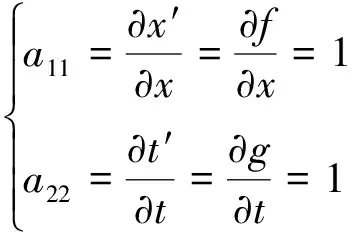
(15a)
(15b)
由于從伽利略變換所導出的預測與接近光速的實驗結果不吻合,所以要對其修改。一種修改就是放寬式(15)的要求。當然,隨意放寬也不盡合理,比如a11=1000就相當于在S的長度單位為m,而S′為mm。因度量單位不一致所造成的差異與物理本質無關。
一個較為合理的拓展是把式(15a)放寬成從S到S′的縮放系數與從S′到S的縮放系數相等,即
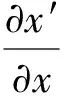
(16)

為了利用式(16), 從式(14)解出
(17)
其中行列式Δ=a11a22-a21a12。由式(17)有
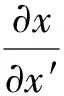
(18)
式(16)變為
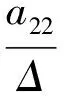
(19)
本文將首先從時空均勻性、時空的各向同性和慣性坐標系的等價性等三性出發,導出線性時空變換,然后再附加進一步的假設,推演洛倫茲變換。
在S′中看到S原點的速度v′為(利用式(25)的第一式和第三式)
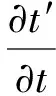
(20)
由式(17)得到

