基于灰色模型的寧波舟山港貨物吞吐量預測研究

鄭浩曄

摘 要： 港口自古以來就是各個國家對外貿易、與其他國家交流溝通的一個重要場景。而港口貨物吞吐量則可以定量地衡量該港口進出口貿易的絕對值以及在整個國家進出口貿易中所占的比重，在一定程度上反映了港口城市以及所在國家的經濟繁榮程度。寧波舟山港是排名世界前五的港口，具有一定的代表性，本文以寧波舟山港貨物吞吐量的近幾年統計數據為依據，利用灰色預測模型科學預測未來寧波港貨物吞吐量。通過實例探討GM（1，1）模型在港口吞吐量方面的應用，同時驗證了灰色預測模型的有效性和實用性。

關鍵詞： 港口吞吐量;灰色預測;GM（1，1）模型;發展策略

中圖分類號：F253????? 文獻標識碼：A????? 文章編號：1008-4428（2018）10-0005-02

一、 引言

隨著世界經濟與貿易的發展，進出口越來越頻繁，而港口則是一座城市甚至一個國家對外貿易的重要場景。港口貨物吞吐量則可以精確定量地衡量該港口進出口貿易的絕對值以及橫向與其他港口作比較，顯示其在整個國家進出口貿易中所占的比重，在某種意義上可以反映出港口城市以及所在國家的經濟繁榮程度。對港口吞吐量的合理預測對港口發展方向、基本設施投資規模、港口的經營策略等方面都有著至關重要的作用。寧波舟山港位于我國海岸中部的杭州灣口南側，距長江口僅200公里，是我國沿海南北海運的交匯處，歷史悠久。2017年，寧波舟山港的貨物吞吐量達到了10.09億噸，成為世界上首個貨物吞吐量超過10億噸的港口。隨著貨物吞吐量的增加勢必意味著基礎設施需要緊跟步伐，與之配套。因此，科學且準確地預測港口貨物吞吐量是必要且實用的。

港口貨物吞吐量預測方法有很多種。比如劉明維等在2005年用指數平滑法進行預測;劉志杰等人在2007年使用組合模型法對港口的貨物吞吐量進行預測;林強等在2008年使用灰色多元回歸模型法;匡海波在2009年用灰色模型法進行預測;陳秀瑛，古浩在2010年使用線性回歸分析法進行預測。由于區域經濟發展狀況、港口運營情況、港口基礎設施、市場需求等錯綜復雜的因素互相作用，影響著港口的貨物吞吐量，其中的關聯實在是讓人難以弄清楚。而灰色系統預測模型恰好適用于信息不完全的場景，因此本文選用灰色系統來預測寧波舟山港的貨物吞吐量，這對其他港口也有著一定的借鑒意義。

二、 模型的建立

（一）灰色模型來源

1982年，華中科技大學控制科學與工程系教授鄧巨龍提出灰色模型這一概念。灰色模型是求解不完全信息系統的一種數學方法。它將控制論的觀點和方法擴展到了相對復雜的大型系統中，將運籌學的數學方法和自動控制融合在一起，以其獨特的角度對廣泛存在于客觀世界中的灰色問題進行研究。在短時間內，灰色系統理論得到了迅速的發展，應用于自然科學和社會經濟等諸多領域，說明了這門學科強大生命力以及合理性，具有廣闊的發展前景。

灰色系統理論研究的是信息不完全的建模問題，為解決信息不完備情況下的系統問題提供了一種新的方法。它把所有隨機過程看作是一個在一定范圍內變化的、與時間相關的灰色過程。灰色模型是通過大量的樣本研究，使用數據生成的方法，而不是從以往人們所熟知的統計規律的角度來看的。它將無序的原始數據按一定數量排序生成序列從而進行研究。灰色理論認為，雖然系統的行為現象是比較混沌的，數據是比較沒有規律可循的，但它具有整體性，在混沌的數據之后，必然有一些規律隱藏在其中。灰色模型的產生就是從無序的原始數據中找尋到這一內在規律。

（二）灰色系統GM（1，1）的具體模型及計算方法

設非負原始序列X（0）={x（0）（1），x（0）（2），…，x（0）（n）}，對X（0）作一次累加，得到生成數列為X（1）={x（1）（1），x（1）（2），…，x（1）（n）}，其中 x（1）（k）=∑ k i=0 x（i）。 于是x0（k）的GM（1，1）白化形式微分方程為

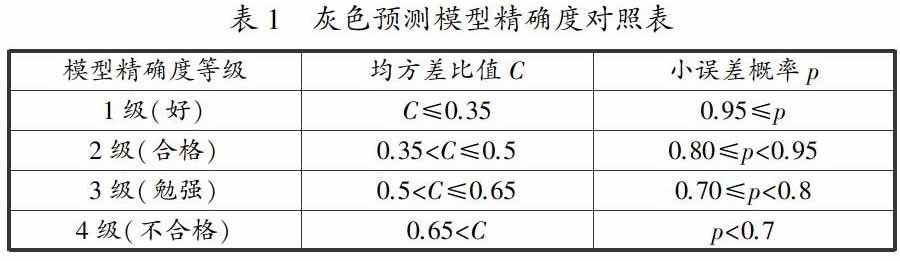
指標均方差比值（16）和小誤差概率（17）是后驗差檢驗的兩個重要指標，均方差比值越小越好，均方差比值越小表示原始序列的方差大而殘差序列的方差越小，即原始數據離散程度大而殘差離散程度小，均方差比值越小就意味著盡管原始數據很離散，而模型所計算出來的值與實際值之差并不太離散。

指標小誤差概率越大越好，小誤差概率越大，表明殘差與殘差平均值之差小于給定值0.6745s1的點較多，也就是說擬合值分布比較均勻。按均方差比值、小誤差概率這兩個指標，可以比較綜合地描述預測模型的精確度。模型的精確度由均方差比值和小誤差概率共同刻畫。一般將模型精確度分為四級，具體見表1。

三、 灰色預測實例分析

（一）寧波舟山港簡介

寧波港因為其地理優勢，作為港口的歷史十分的悠久。早在唐朝的時候，當時稱為明州港的寧波港就開始有前往高麗、日本和南洋等地的國外航線，在宋朝和元朝時期，明州港作為海上絲綢之路的起點，更是和廣州港、泉州港一起稱為三大貿易港口，由此可見其規模之大名聲之響。近現代以來，從作為《南京條約》五口通商口岸之一到改革開放以后，寧波被列為計劃單列市大力發展對外貿易的重要戰略舉措，無不彰顯著這座城市、這個港口的悠久歷史、良好的地理位置。

從近幾年的數據看，寧波港被列為世界五大港口，中國前三大港口，其中寧波港的貨物吞吐量位居全國第一，集裝箱吞吐量列為全國第三。2016年1月1日起，寧波港與附近的舟山港完成合并，取名為寧波舟山港。這一合并增加了寧波舟山港在國際貿易中的地位，有著深遠的戰略意義。

2017年全年，寧波港累計完成了10.09億噸的貨物吞吐量，成為全球第一個且唯一一個貨物吞吐量超10億噸的大港，坐上了世界第一的寶座。

（二）寧波舟山港貨物吞吐量預測

寧波港近八年貨物吞吐量如下表2所示：

以2010—2017年寧波港貨物吞吐量為基期數據進行預測，原始時間序列數據X（0）={6.33，6.94，7.44，…，10.09}， 累加序列X（1）={6.33，13.27，20.71，…，65.74}，可以求得a=-0.057760，u=6.519640，進一步灰微分方程的白化方程是：dx（1）/dt-0.057760x（1）=6.519640。

時間響應式最終整理得：

X（1）（k+1）=119.205188exp（0.057760k）-112.875188，

代入可得：X（1）=（6.33，13.417989，20.927433，28.883391，37.312414，46.242630，55.703840，65.727618），X（0）=（6.33， 7.087989，7.509444，7.955958，8.429023，8.930216，9.461210，10.023778）

檢驗誤差：①均方差比值C=s2/s1=0.08≤0.35，預測結果為好，②小誤差概率p=100 % ≥0.95，預測結果為好。同時根據此模型對之后五年寧波港的貨物吞吐量進行預測結果見表3。

四、 結論

本文以寧波港為例，利用灰色系統預測模型對其集裝箱吞吐量進行預測。預測顯示，到2020年寧波舟山港的貨物吞吐量將達到11.92億噸。

預測結果顯示，寧波舟山港貨物吞吐量增長迅速、市場前景良好。作為當地政府以及有關部門，首先需要保證城市的規劃以及對貿易公司、出口企業的大力扶持，只有經濟保持強有力的增長，港口才會有源源不斷的貨物需要運輸。另外寧波港應該積極改善港口基礎設施，營造良好的經營環境，制定與吞吐量迅速增長相適應的港口規劃，一定不要讓港口的硬件設施掣肘了港口的規模以及發展。在貨物吞吐量保持高速增長的前提下，政府需要著手協調好港口日益增長的運輸需求與港口本身供給能力不足之間的矛盾，牢牢占據住港口貨物總吞吐量世界排名第一的寶座。

參考文獻：

[1]陳濤燾，高琴.港口集裝箱吞吐量影響因素研究[J].武漢理工大學學報，2008（12）.

[2]劉明維，王鐸銀等.港口貨物吞吐量預測方法探討[J].水運工程，2005（3）.

[3]劉志杰，季令，葉玉玲等.基于徑向基神經網絡的集裝箱吞吐量組合預測[J].同濟大學學報（自然科學版），2007.

[4]林強，陳一梅.灰色多元回歸模型在港口吞吐量預測中的應用[J].水運工程，2008（7）.

[5]匡海波.中國沿海港口吞吐量預測模型研究[J].科研管理，2009.

[6]陳秀瑛，古浩.灰色線性回歸模型在港口吞吐量預測中的應用[J].水運工程，2010（5）.

[7]鄧聚龍.灰預測與灰決策[M].武漢：華中科技大學出版社，2002.

[8]劉思峰.灰色系統理論及其應用[M].北京：科學出版社，2005，6.