混合遺傳模擬退火算法求解旅游線路優化問題

黃華升+張波

摘 要：廣西旅游資源豐富，對出行線路的規劃可以能讓旅游線路更為優化合理。本文以廣西30個城市的旅游線路優化問題構造TSP問題，分析了遺傳算法和模擬退火算法的優缺點。利用兩種算法的互補性，構造了混合遺傳模擬退火算法，指出三種算法對旅游線路的求解算法過程。通過對實驗數據的對比分析，得出了混合遺傳模擬退火算法在求解精度上優于遺傳算法或模擬退火算法。

關鍵詞：混合遺傳模擬退火算法；旅游線路優化；TSP問題

中圖分類號：TP399 文獻標識碼：A

Abstract：Due to the abundant tourism resources in Guangxi，reasonable route planning can effectively optimize the travel schedule.The paper constructs TSP problems of tourist route optimization for 30 cities in Guangxi province.The paper analyzes the advantages and disadvantages of the genetic algorithm and the simulated annealing algorithm.Making use of the complementarity of the two algorithms，the paper constructs a hybrid genetic simulated annealing algorithm，and proposes the solution procedures of tourist route optimization with the three algorithms.Through the comparative analysis of experimental data，it is concluded that the hybrid genetic simulated annealing algorithm is superior to the genetic algorithm and the simulated annealing algorithm in solution accuracy.

Keywords：the hybrid genetic simulated annealing algorithm；tourist route optimization；TSP problems

1 引言（Introduction）

遺傳算法是一種通過模擬自然進化過程如適者生存、優勝劣汰遺傳機制而來的搜索最優解的啟發式算法。遺傳算法適應能力強，但是存在著“早熟”的問題，也就是空間的探索能力有限，很容易收斂到局部最優解，無法達到全局最優。模擬退火算法也是一種隨機尋優智能算法，其借助金屬固體退火過程的原理，設定高的初溫度，采用Meteropolis接受準則，以一定的溫度參數不斷降低溫度，能有效避免陷入局部極小，得出一個近似最優解。但模擬退火算法也有收斂速度慢、執行時間長等問題。遺傳算法和模擬退火算法具有較強的互補性，將兩種算法組合在一起發揮各自優勢，避免缺陷，就形成了混合模擬退火遺傳算法，簡稱MGASA[1-3]。

2 廣西旅游線路優化問題（Optimization of tourist

routes in Guangxi）

廣西旅游資源豐富，要實現瀏覽一遍廣西所有旅游資源需要合理安排旅游線路。廣西旅游線路優化就是選取廣西的30個城市瀏覽一遍，要求每個城市有且僅經過一次，這樣的一條旅游的最短路線就是我們的優化目標[4]。這個問題的實質就是構造廣西旅游線路優化的TSP問題。廣西30個旅游城市的坐標見表1。

TSP問題是比較典型的組合優化問題，求解方法主要有線性規劃法、分支定界法、遺傳算法和模擬退火算法等。但這些常規的算法往往存在一些弊端，本文使用混合模擬退火遺傳算法，通過對比實驗的方式來求廣西的30個城市的旅游線路最優解。

3 算法比較（Algorithm comparison）

3.1 遺傳算法求解旅游線路優化問題

遺傳算法是搜索最優解的啟發式算法，使用遺傳算法求廣西旅游線路過程描述如下：

步驟1初始化種群：設置染色體長度n，初始化種群的規模nind。

步驟2適應度函數計算。

步驟3選擇操作：選擇適應度高的染色體。

步驟4交叉操作：采用部分映射雜交，確定交叉操作的父代，將父代樣本兩兩分組為p1和p2，每組重復如下操作。第一，產生[1，30]區間內的隨機整數p1和p2，確定兩個位置，對兩個位置的中間數據進行交叉。第二，交叉后，同一個個體中有重復的城市編號，不重復的數字保留，有沖突的數字利用中間段的對應關系進行映射的方法消除沖突。

步驟5變異操作：隨機選取兩個點，將其對換位置。產生[1，30]范圍內的隨機整數r1和r2，確定兩個位置，將其對換位置。

步驟6進化逆轉操作：產生兩個[1，30]區間的隨機整數r1和r2，確定兩個位置，將其對換位置。

步驟7檢查判斷是否滿足設定的最大遺傳代數MAXGEN，不滿足則跳入適應度值的計算；否則，結束遺傳操作[5，6]。

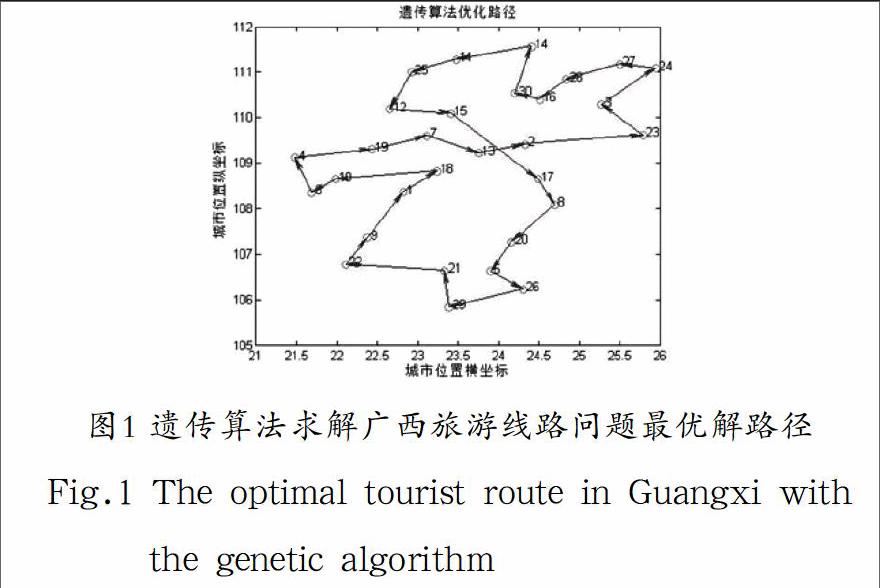
實驗的初始變量交叉概率為0.9，變異概率為0.05，代溝為0.9，分組后得到的最短路徑為：25.267。最短路徑是[1 9 2221 29 26 5 20 8 17 23 24 27 3 16 28 14 11 30 2 13 7 15 25 12 19 4 6 10 181]。路徑如圖1所示。

3.2 模擬退火算法求解旅游線路優化問題

模擬退火算法是模擬固態物體降溫過程，解決一般組合優化問題的優化算法。基于模擬退火算法的TSP問題求解具體步驟如下：

步驟1設置算法參數：初始溫度T0，降溫系數q，結束溫度Tend和鏈長L；設置代數計數器初始化，t=0。

步驟2初始解：使用randperm函數產生隨機初始線路。

步驟3解變換生成新解：采用產生隨機數的方法產生兩個要交換的城市，用二領域變換法產生新的路徑，確定新的可行解S'。

步驟4Metropolis準則：計算增量Δt'=C（S'）-C（S），其中C（S）為評價函數。根據Metropolis準則，如果增量Δt'<0，則以S'接受新的路徑；如果Δt'>=0，則以概率exp（-Δt'/T）接受新的路徑。

步驟5降溫：如果滿足終止條件，則輸出當前解作為最優解，結束程序。否則轉步驟3繼續迭代。

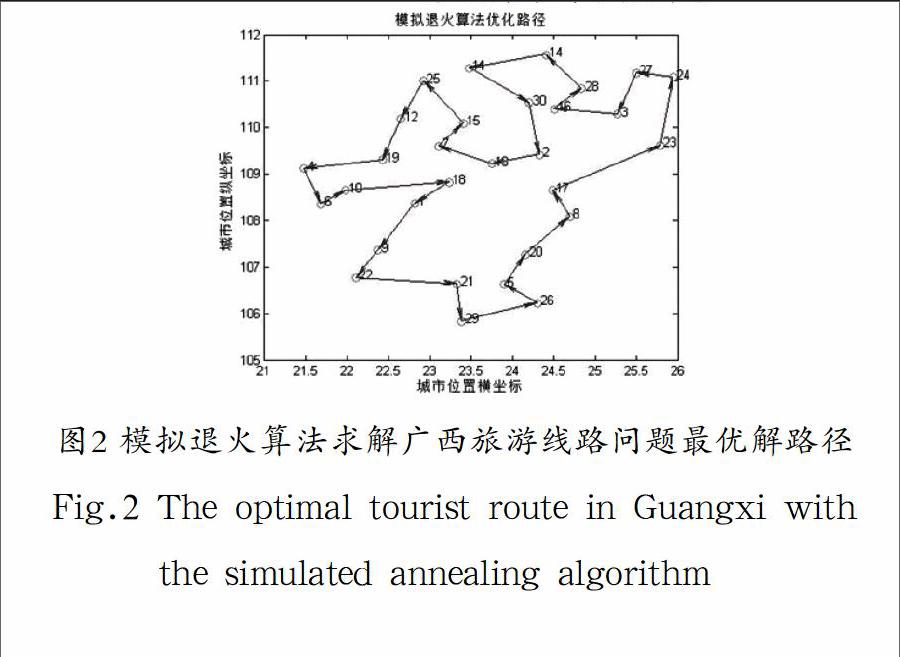
實驗參數設置為降溫速率0.9，初始問題1000，結束溫度0.001，鏈長200，最后最短路程為：26.1658。最短路徑是[[1 18 10 6 4 19 7 13 2 23 324 27 28 16 30 14 11 25 12 15 17 8 20 5 26 29 21 22 9 1]。路徑如圖2所示。

3.3 混合遺傳模擬退火算法求解旅游線路優化問題

遺傳算法的優點是快速隨機的搜索能力，缺點是容易“早熟”，局部搜索能力較差；而模擬退火算法的優點是具有較強的局部搜索能力。因此將模擬退火算法和遺傳算法結合起來，取長補短就能形成更為合理的優化問題的優化算法，這就是混合遺傳模擬退火算法。使用混合遺傳模擬退火算法求解廣西旅游線路優化的方法過程描述如下：

步驟l初始化：設置種群F（k）的初始值，設置初始退火溫度t0，設置降溫系數a等；設置代數計數器初始化，t=0。

步驟2隨機產生初始群體F（k）的適應度。

步驟3計算F（k）中個體的適應度，執行個體交叉操作，采用淘汰算法進行最優個體保存，到新的群體Fl（k）。

步驟4執行個體變異操作，得到新的群體F2（k）。

步驟5采用模擬退火規則產生新的種群。

步驟6執行個體的模擬退火操作得到F3（k）。

步驟7判斷模擬退火抽樣是否穩定，如果不穩定，返回步驟5；如果穩定，繼續執行退溫操作。

步驟8個體的選擇復制操作，F（k+1）=Re_Produce[F（k）F3（k）]。

步驟9如果滿足終止條件，輸出當前最優解，結束程序；否則k=k+l，轉步驟2，繼續進化過程[7，8]。

實驗設置初始種群規模為50，終止溫度為1，降溫系數為0.5，初始溫度為70，最后最短路程為：23.9795。最短路徑是[1 9 22 21 29 26 5 20 8 17 2324 27 3 1628 14 1130 2 13 7 15 25 12 19 4 6 10 18 1]。路徑如圖3所示。

3.4 實驗分析

將每種算法進行10次計算，最后結果數據對比見表2。

由實驗數據對比可以看出，使用混合遺傳模擬退火算法計算的最佳解、最差解及平均解在三種算法中都是最小，平均進化代數也是最小的，因此使用混合遺傳模擬退火算法是能有效提高對線路優化問解的求解精確度。

4 結論（Conclusion）

本文分別使用遺傳算法、模擬退火算法、混合遺傳模擬退火算法三種算法對旅游線路的優化問題進行計算，從數據的對比分析來看，混合遺傳模擬退火算法能夠較快地收斂并獲得全局最優解，在精準度上比單一的遺傳算法和模擬退火算法要高。下一步還需要繼續探究混合遺傳模擬退火算法中的參數設置對算法性能的影響，找出參數與求解旅游線路優化之間的邏輯聯系，以獲得更優的精度解。

參考文獻（References）

[1] 劉錦.混合遺傳算法和模擬退火算法在TSP中的應用研究[D].廣州：華南理工大學，2014：30-53.

[2] 崔穎.排水管道設計優化的遺傳與模擬退火混合算法研究[D].重慶：重慶大學，2009：39-43.

[3] 丁書斌.基于混合遺傳算法的車間調度方法研究與應用[D].大連：大連理工大學，2006：23-32.

[4] 姚君.遺傳模擬退火算法——黑龍江TSP問題[J].價值工程，2016，35（36）：206-208.

[5] 郁磊，史峰，王輝，等.MATLAB智能算法30個案例分析[M].北京：北京航空航天大學出版社，2010：38-187.

[6] 曹小鳳.基于遺傳算法的藥物療效評價模型研究[J].軟件工程，2017，20（05）：39-42.

[7] 劉懷亮，劉淼.一種混合遺傳模擬退火算法及其應用[J].廣州大學學報（自然科學版），2005（02）：141-145.

[8] 喬彥平，張駿.基于一種改進遺傳模擬退火算法的TSP求解[J].計算機仿真，2009，26（05）：205-208.

作者簡介：

黃華升（1978-），男，碩士，高級工程師.研究領域：軟件開發.

張 波（1983-），男，碩士，講師.研究領域：自然語言處理.