基于驗前信息的改進Bootstrap導彈命中精度評定方法?

宋貴寶 劉澤坤 羅亞民 李一夫

1 引言

Bootstrap自助法實質是利用重抽樣技術來評估不確定性，利用再生子樣對未知參數進行統計推斷，其關鍵在于獲得可信程度高的再生子樣。Bootstrap自助法是一種對中等數量規模的樣本進行統計推斷的較優方法，在小子樣和特小子樣條件下再生子樣可信度不高［1］。

新時期條件下，導彈更新換代速度加快、單枚造價高昂。針對導彈命中精度進行的評定試驗，現場試驗次數和觀測數據少，直接運用Bootstrap法，產生的再生子樣重復率高，其統計推斷結果偏差較大。同時，在導彈生產定型階段存在著大量的驗前信息。如何利用驗前信息去擴充現場試驗觀測樣本，改進Bootstrap自助法再生子樣的獲取方式，提高再生子樣的真實程度，是一個值得研究的問題。

基于此，本文針對對地攻擊導彈命中精度的評定問題，選取圓概率偏差CEP指標，采用非參數Bootstrap法，通過利用各類通過相容性檢驗的驗前信息來完善現場試驗觀測樣本，并引入重要度抽樣的思想，保護更為寶貴的原始觀測樣本數據，提高再生子樣的真實程度和最終評定結果準確性。

2 命中精度評定試驗指標

2.1 圓概率偏差CEP

命中精度表現了導彈武器系統彈藥相對于固定目標點的落點散布特性，客觀反映了導彈武器系統對目標的命中能力。對戰術彈道導彈和攻擊地面目標的飛航導彈進行命中精度的評定，其實質就是通過獲取各類試驗信息，對導彈武器系統的命中精度進行統計推斷。其中，圓概率偏差（CEP）是導彈武器系統命中精度評定最常用的指標。

圓概率偏差（CEP）指的是在穩定的發射條件下，向目標發射的導彈武器系統，有50%概率落入以期望彈著點（散步中心）為圓心、R為半徑的散布圓（等概率圓）內，該散布圓半徑R即為圓概率偏差CEP［2］。

針對平面目標射擊，以目標為圓心，射擊方向為縱軸，垂直于射擊方向為橫軸，（X，Z）表示落點偏差坐標并服從正態分布，縱橫向獨立，（X，Z）～N（μX，μZ，σ2X，σ2Z）。如下式所示：

式中，當P=50%時，R即為圓概率偏差CEP；μX、μZ為縱橫向射擊準確度（系統誤差）要求，σX、σZ為縱橫向射擊密集度（標準差）要求，因此圓概率偏差CEP可綜合反映四個指標（μX，μZ，σ2X，σ2Z），能夠很好的融合射擊準確度和密集度進行表征。

2.2 命中精度縱橫向聯合檢驗

從工程應用的角度考慮，對圓概率偏差CEP進行評定，直接尋找相關統計量較為困難。一般來說，由于系統誤差可采用各種手段進行補償修正，當系統誤差遠小于隨機散布偏差時，對導彈命中精度CEP的評定試驗，可轉化為對射擊密集度（標準差）σ的評定。

假定系統誤差造成的落點偏差經過補償修正，射擊無系統誤差，且落點散布為圓散布。對落點偏差坐標（X，Z），有X ～ N（0，σ2X），Z ～ N（0，σ2Z）。

記σ2X?DX，σ2Z?DZ，則對于圓概率偏差CEP的評定，可轉化為對射擊密集度σ的評定［3］，且當σX= σZ= σ0時，可得：

當σX≠σZ時，可得：

3 Bootstrap自助法

3.1 Bootstrap法原理

設某型導彈靶場試驗現場觀測i.i.d.樣本X=｛X1，X2，…，Xn｝來自未知總體分布，Xi～ F（x），θ=θ（F）是總體分布F的未知數，由子樣X1，X2，…，Xn作經驗分布Fn，= ( )

Fn為θ的估計，記估計誤差：

將估計值 θ(j)(F )作為θ（F）的子樣，可作出θ（F）的抽樣分布，并由此出發，作出關于θ的統計推斷［4～6］。

3.2 再生子樣獲取的抽樣方法

獲取再生子樣，首先要確定抽樣分布函數Fn。根據分布函數Fn中是否含有待定參數，再生子樣的抽樣方式可分為非參數抽樣和參數抽樣。這里介紹非參數抽樣法。

將獲得的i.i.d子樣X1，X2，…，Xn按從小到大排序，可得 X=｛X（1），X（2），…，X（n）｝，且X（1）≤ X（2）≤ … ≤ X（n）。可構造經驗分布函數如下［7］：

產生服從該經驗分布函數的再生子樣步驟如下：

每次產生一個［1，n］區間上均勻分布的隨機整數η，則可根據η產生新的樣本點X（η）；重復該過程n次，可得到一組再生子樣X*。

由經驗分布函數可知，每個樣本點Xi都有相同的被抽中概率，特別是抽樣次數很大時，每個樣本點的出現頻率都趨近于 1/n［8］。

3.3 區間估計

對于參數θ，假定根據Bootstrap法產生的i組再生子樣所獲得的關于θ的參數估計為j* ，將j*按照大小順序排列，可得：

因此，給定某一水平α，通過區間截取，可獲得置信度水平為1－α的Bootstrap區間估計為

4 小子樣條件下改進Bootstrap法

非參數Bootstrap抽樣法中產生的新的再生子樣均包含在原樣本中，且當原樣本數量足夠時，產生的再生子樣中包含有重復子樣的概率極低。但是該方法的缺陷在于，當待抽樣的原樣本的數量較少時，尤其是小子樣、特小子樣情況下（如n≤5），重抽樣的再生子樣會出現“退化”現象，即會多次出現兩組子樣相同的情況［9］。

因此考慮利用可信的驗前信息，對現場試驗數據進行補充，擴大待抽樣的原樣本容量，并引入重要度抽樣的思想保護現場試驗數據，提高Bootstrap方法產生的再生子樣與真實分布的相符合程度。

4.1 驗前信息相容性KS檢驗

導彈在生產定型等過程中的驗前信息種類繁多。在應用這些驗前信息前，必須對驗前信息和現場試驗信息進行相容性檢驗，本節采用KS檢驗法。

假定有來自于總體分布F（x）的樣本：

其經驗分布函數為Fm（x）。

另有來自總體分布G（y）的樣本：

其經驗分布函數為Gn（y）。

取檢驗統計量

并給定顯著性水平α，若

則可認為兩樣本不屬于同一總體，否則屬于同一總體。式中

Dl，α可通過查找柯爾莫格洛夫檢驗臨界值表得出。

4.2 基于驗前信息的改進Bootstrap抽樣

假定有n組現場觀測數據為

且(Xi，Zi) ～ N（0，0，σX2，σZ2）。另有NF組已經通過顯著性水平為α的KS檢驗的驗前信息落點偏差數據為

為避免現場試驗數據被大量驗前信息所“湮沒”，引入重要度抽樣的思想［10～11］，根據不同類信息源的臨界檢驗水平αL（即超過該水平無法通過相容性檢驗）來映射信息源的置信度ωi。

工程上相容性檢驗的水平一般取0.1～0.4，因此采用以下從臨界檢驗水平αL到置信度ωi的線性映射：

假定存在p類驗前信息源，每類信息源的臨界檢驗水平為 αL(i)（i=1，2 ，…，p），則有線性映射：

根據置信度確定重要度。先令現場試驗子樣本的置信度ε0為1，則p類驗前信息源的重要度為

將上述兩組數據相混合，可以得到能夠產生再生子樣X*的待抽樣樣本：

現場試驗子樣本的重要度為

4.3 改進區間估計法

針對傳統區間估計方法估計效率不高，且總體分布非對稱時效果不佳的不足，本節采用Bootstrap-t區間估計法。

Bootstrap-t區間估計相關步驟如下：

1）根據觀測子樣X獲得參數θ的估計值 和標準差 se()；

2）由經驗函數再抽取k組再生子樣本為

并由各子樣本分別獲得估計值 *i和估計標

3）取統計量

并根據大小順序排列 t*i，得到

則給定某一水平α，通過區間截取，可獲得置信度水平為1－α的Bootstrap區間估計為

5 實例分析

某型對地攻擊導彈進行命中精度評定，經過現場靶場試射，得到5組真實縱橫向落點偏差值數據，且服從正態分布N（0，502），具體數據見表1。

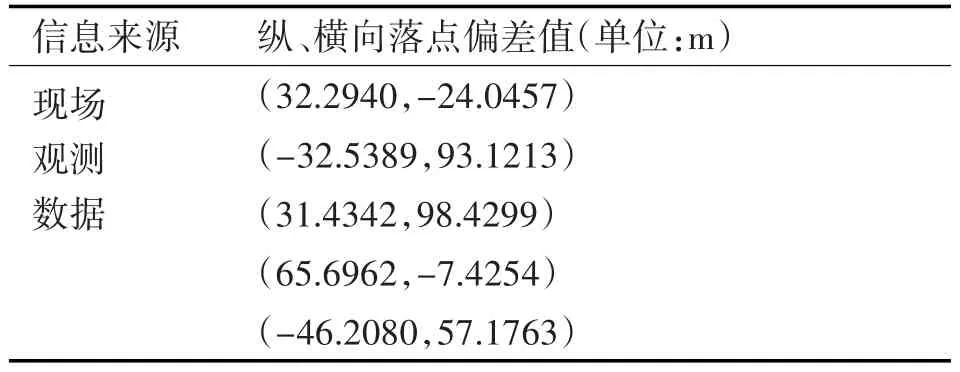
表1 現場觀測樣本數據

另有兩類通過了KS相容性檢驗的驗前信息，一類是改進前相似型號試射的6組驗前數據（臨界檢驗水平αL1為0.1），另一類是模擬彈道仿真試驗的6組驗前數據（臨界檢驗水平αL2為0.2），兩類驗前數據均服從正態分布N（0，552），具體數據見表2、表3。

根據式（16）線性映射，可得相似型號試射信息的置信度為1/2，彈道仿真信息的置信度為2/3；

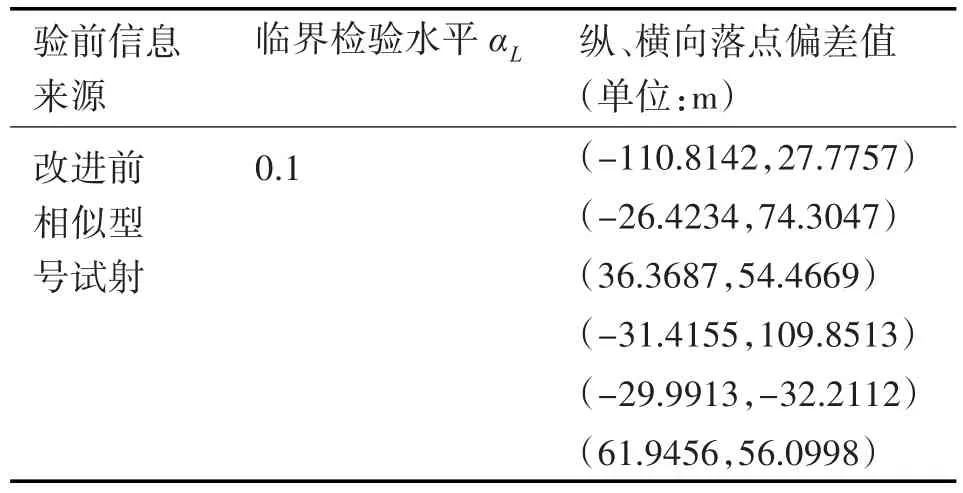
表2 改進前相似型號試射驗前信息數據

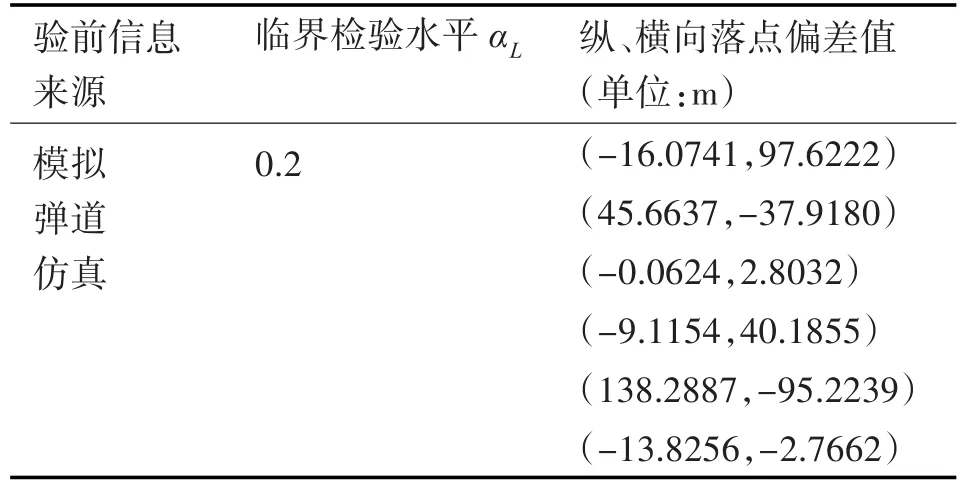
表3 模擬彈道仿真驗前信息數據

根據式（17）、式（18），可得相似型號試射驗前信息分配權重為

彈道仿真信息分配重要度為

現場真實數據分配重要度為

因此，相似型號試射驗前數據的6個子樣本每個被抽中概率約為0.038；彈道仿真信息的6個子樣本每個被抽中概率約為0.052；現場真實數據5個樣本，每個被抽中的概率約為0.092。

根據圖2仿真步驟進行抽樣，設定再生子樣的容量為20（即每20個新產生的數據為一組再生子樣），共抽取2000組。由獲得的子樣本相關數據，分別進行縱、橫向射擊密集度（標準差）點估計、置信度80%的區間估計以及計算圓概率偏差CEP值。仿真步驟如下：

根據仿真流程，所獲得的仿真結果與分析結論如下：

1）基于驗前信息的改進Bootstrap法與經典統計方法的仿真結果見表4。

分析可知，經典統計方法直接應用現場觀測樣本與驗前信息共17個樣本數據，該方法并不產生再生子樣，其σX與σZ的點估計要大于采用重要度抽樣的自助法的σX與σZ的點估計，且經典統計方法區間估計遠不夠精確，如σX的80%置信區間估計，經典統計方法的［46.4407，73.8400］區間范圍遠大于自助法的［42.3384，61.5753］區間范圍；

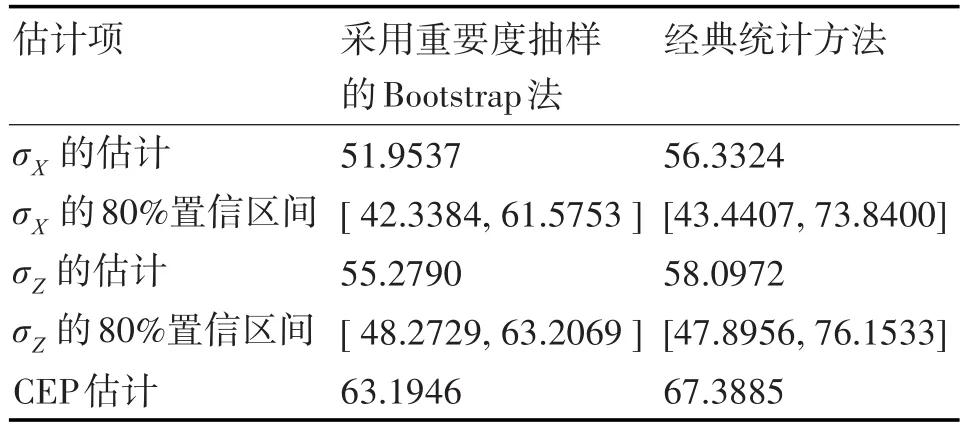
表4 縱、橫向射擊密集度σ估計結果（1）

2）采用重要度抽樣的Bootstrap法與不采用重要度抽樣的Bootstrap法的統計推斷數據見表5。

表5 縱、橫向射擊密集度σ估計結果（2）

分析可知，相比于不采用重要度抽樣，采用重要度抽樣的評估結果更接近現場觀測樣本的分布特征，如σX的點估計51.9537更接近σ0的估計值50；σX的80%置信區間估計［42.3384，61.5753］比區間［43.5150，64.6456］更接近正態分布 N（0，502）；

3）射擊密集度σ分布（以σX為例）見下圖3、4。

分析可知，采用重要度抽樣的改進自助法，其射擊密集度σX的區間（總體）分布更近似于正態分布，且σX的點估計和區間估計，更接近于現場觀測樣本的分布N（0，502），其真實性和可信程度更好。

綜上可知，在小子樣條件下，基于驗前信息的改進Bootstrap法所產生的再生子樣，其可信程度比改進前Bootstrap法產生的再生子樣可信度更高，其統計推斷結果相比于經典統計方法也更加得精確，因此該方法能夠為小子樣條件下導彈命中精度的評定提供一種可供參考的結果。

6 結語

本文結合某型對地攻擊導彈的現場試驗數據，選取射擊密集度σ作為命中精度評定指標，針對非參數Bootstrap法不適用于小子樣條件下統計推斷的缺陷，通過綜合利用各類真實的驗前信息數據，引入重要度抽樣思想，對Bootstrap再生子樣的獲取方式進行改進。仿真結果表明，基于驗前信息的改進Bootstrap法所獲得的σ估計與置信區間，其結果的真實性更好，能夠為導彈命中精度評定試驗提供一定的參考。

當然，Bootstrap自助法作為一種原始樣本信息的“提攜”手段，在小子樣甚至特小子樣條件下應用，存在著許多可以改進之處。如現場數據的大致分布已知時能否采用參數Bootstrap法（原始樣本仍是小子樣條件），落點縱橫向偏差非獨立時如何應用驗前信息，各類驗前信息的重要度如何更好地進行分配，再生子樣的容量如何設定才能更加合理等。這些問題值得進行更為深入地研究。

［1］唐雪梅，蔡洪，楊華波等.導彈武器精度分析與評估［M］.北京：國防工業出版社，2015：250-263.

［2］王正明，盧芳云，段曉君等.導彈試驗的設計與評估［M］.北京：科學出版社，2010：438-440.

［3］張宗梅，宋維軍，李雙喜等.一種融合驗前信息的特小子樣精度評估方法［J］.航天控制，2011，29（6）：49-53.

［4］Davison，A.C.（Anthony Christopher），Hinkley，D.V.Bootstrap Methods and Their Application［J］.Technometrics，1997，42（2）：216-217.

［5］雷鳴，張麗群.基于Bootstrap方法的艦空導彈武器系統制導精度評定［J］.現代防御技術，2014，42（5）：60-64.

［6］劉新愛，陳勇男，王如根.基于自助法的導彈命中精度評定［J］.戰術導彈技術，2004（06）：32-34.

［7］孫錦，李國林等.基于Bootstrap的反艦導彈靶場試驗小樣本數據分析方法研究［J］.計算機與數字工程，2014，42（1）：48-51.

［8］Pérez M C I，Manteiga W G.Bootstrap for the conditional distribution function with truncated and censored data［J］.Annals of the Institute of Statistical Mathematics，2003，55（2）：331-357.

［9］劉思雨，張敏強.Bootstrap平均數假設檢驗樣本容量探討［J］.統計與決策，2016（14）：26-28.

［10］唐雪梅，李榮，胡正東等.武器裝備綜合試驗與評估［M］.北京：國防工業出版社，2013：33-82

［11］胡正東，曹淵，張士峰等.特小子樣試驗下導彈精度評定的Bootstrap方法［J］.系統工程與電子技術，2008，30（8）：1493-1497.

［12］劉建，吳翊，譚璐.對Bootstrap方法的自助抽樣的改進［J］.數學理論與應用，2006（1）：71-74.

［13］Duan X.APPLICABILITY OF BOOTSTRAP METHOD IN SMALL SAMPLE CASE［J］.Journal of Ballistics，2003（3）：1-5.

［14］金振中，李曉斌等.戰術導彈試驗設計［M］.北京：國防工業出版社，2013：96-143

［15］郭齊勝，羅小明，潘高田.武器裝備試驗理論與檢驗方法［M］.北京：國防工業出版社，2013：188-191.

［16］GJB5207-2004.地地戰術導彈批抽檢飛行試驗驗收方法［S］.國防科學技術工業委員會批準，2004.

［17］GJB2899-97.飛航導彈飛行試驗精度分析和命中精度評定方法［S］.國防科學技術工業委員會批準，1997.

［18］樊立明，吳鵬，萬偉.基于Bayes自助法的小子樣命中精度評估［C］//The International Conference on Computational Intelligence and Industrial Application.2010：3-4.

［19］曹裕華.裝備試驗設計與評估［M］.北京：國防工業出版社，2016：183-189.

［20］徐英，王松山，柳輝等.裝備試驗與評價概論［M］.北京：北京理工大學出版社，2016：29-46.

［21］趙喜春.導彈命中精度綜合鑒定方法研究［J］.現代防御技術，2008，36（3）：33-36.

［22］謝紅衛，孫志強，李欣欣等.多階段小樣本數據條件下裝備試驗評估［M］.北京：國防工業出版社，2016：156-167.