基于消費者心理學的尖峰電價模型研究

季露，張靠社，張剛，王永慶

（1.西安理工大學，陜西西安 710048；2.國網陜西省電力公司電力科學研究院，陜西西安 710100）

基于消費者心理學的尖峰電價模型研究

季露1，張靠社1，張剛1，王永慶2

（1.西安理工大學，陜西西安 710048；2.國網陜西省電力公司電力科學研究院，陜西西安 710100）

隨著我國經濟飛速發展，電力需求持續增長，需求側響應（DR）能夠使電力資源得到更加充分地利用，并且適應電力市場的發展。通常利用價格信號或激勵作用來使用戶的用電方式發生改變，從而保障電網的穩定。目前，通過價格信號刺激用戶的方式普遍被運用，通常有3種形式[1]：實時電價（RTP）、分時電價（TOU）、尖峰電價（CPP）。

目前TOU被普遍應用。這種運作模式是在3個不同時期發布3種不同的價格，在電力低谷價格相應降低，在電力高峰提升價格，用電平常時期可以讓電價保持不變，用該方法來誘使人們改變以往對電力的需求。但是，TOU存在以下不足。第一，該機制的單一性硬性特征很難滿足現電力用戶數目龐大、消費形式多樣性的特點；第二，峰谷電價一般會使實施方的銷售收入減少，會減弱實施方在執行該機制時的積極性；第三，執行該機制會使一部分用戶方的電費支出增大，導致機制更難執行[2]。

在國外，有些機構會在大型工業、商業和居民用電執行CPP，依據統計數據可以看出，不管是工業、商業，還是居民，CPP都取得了舉世矚目的成果。比如，尖峰日的高峰時段負荷減少量是非尖峰日的2倍，而且比對照組的普通家庭減少43%的負荷[3]。

在國內，CPP的研究較少。從嚴格意義上來說，CPP的研究是基于峰谷電價之上的。文獻[4]對數據的處理采用支持向量機（SVM）回歸方法，從而得到用戶在TOU下的響應模型。這是一種非機理建模方法。文獻[5-6]都是基于電力需求價格彈性矩陣建立尖峰電價模型，利用遺傳算法進行優化。

目前所研究的CPP一般都是通過時段的差異，制訂不同的電價，從而引導用戶改變用電習慣，起到了削峰填谷、節約負荷側資源、電力成本下降的作用[7]。普遍有2種研究方法，分別是利用統計學原理與電力需求價格彈性矩陣。可是，兩者都沒有提到用戶對電價的響應有著可行性范圍，即電價過低與過高都不會改變用戶的用電習慣。

本文提出了一種考慮消費者對電價反應能力的CPP模型。劃分尖峰時段，以TOU為根本，將1 d劃分成4個時段，從而獲到6種CPP的負荷轉移率，進而得到負荷轉移模型，并進行求解。算例表明，本文方法能夠達到削峰填谷的效果，可減少國家對電力建設的投資。

1 尖峰電價時段的劃分

TOU通常把每天分成3個時段，而本文CPP在峰谷電價的基礎上多分出一個時段，稱為尖峰時段。

模糊隸屬函數被用來確定每個時段的界限[8]。每個時段分界限的原則如下：根據日負荷曲線，可以直觀的選取2個點，即最大負荷點與最小負荷點。最大點必處于高峰時段，而最小點必屬于低谷時段。還有剩余各點所處時段的可能性由半梯形隸屬函數來計算。其原理是計算出各時刻的負荷量在最大負荷量中所占的比例或在最小負荷量中所占的比例，根據該比例初步確定出各個時段。

圖1為偏小型半梯形隸屬函數示意圖，以此來判斷某一時間是否屬于低谷時段，如式（1）所示。式（1）中，a為最小值，b為最大值。當x小于a時，其處于低谷的可能性為1；當x大于b時，處于低谷時段的可能性為0。圖2為偏大型隸屬函數示意圖，利用式（2）來判斷時間點是否屬于高峰時段。當x小于a時，處于高峰時段的可能性為0，當x大于b時，處于高峰時段的可能性為1。

圖1 偏小型半梯形分布Fig.1 The distribution of small and semi trapezoidal

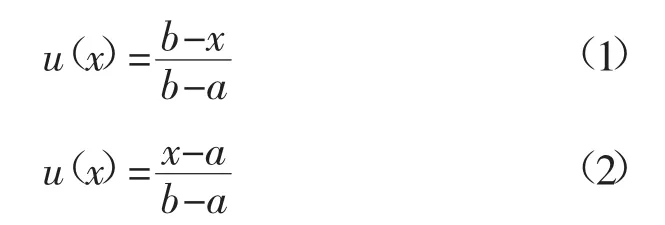
經過對數據的處理，可以進行各時段的劃分。各個時段的時間間隔不能選定的太短，盡量平均分配。可以將平時段、低谷時段均設定為8 h，再將高峰時段與尖峰時段各分為4 h，這樣就得到了CPP模型的時段劃分。

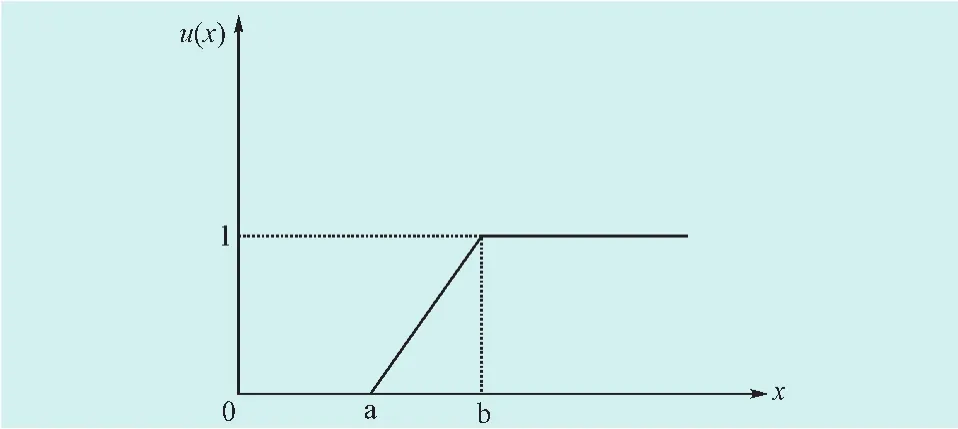
圖2 偏大型半梯形分布Fig.2 The distribution of large and semi trapezoidal

2 尖峰電價作用機理模型

據消費者心理學可知，用戶對電價有一個反應范圍，敏感程度與電價差大小呈線性關系。當電價低于此范圍的時候，價格的刺激就會很微弱，用戶會認為沒必要做出反應，這時電價范圍稱為死區；相反的，電價高于該范圍時，用戶將不再有多余的可轉移負荷，響應能力趨近飽和，與電價的大小無關，稱為響應飽和區[9]。用戶行業的區別會導致負荷轉移的不同，這時需要依據歷史數據擬合出與用戶真實響應度曲線逼近的轉移率曲線。該曲線為線性分段函數曲線，如圖3所示。

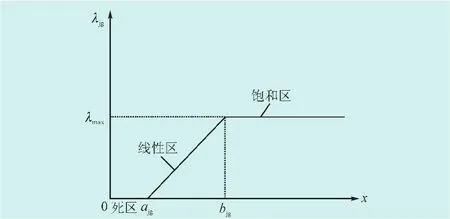
圖3 負荷轉移率的示意圖Fig.3 Load transfer rate representation

對于用戶尖峰時段到谷時段的負荷轉移率可表示為[10]

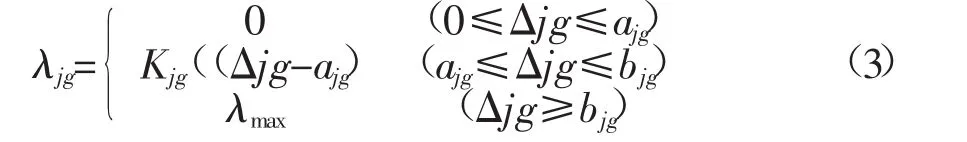
式中：Δjg=Pj-Pg指尖-谷的電價差；ajg為尖-谷負荷能夠有所轉移最小電價差，為其中一個未知變量；點（bjg，lmax）代表的是尖-谷能夠轉移負荷的極限點；λmax為該曲線中的極限轉移率；bjg為負荷極限轉移率所對應的最小電價差，第2個未知變量；Kjg為負荷轉移過程中的線性斜率，也就是第3個未知變量。通過對這3個變量的擬合，就能夠得到CPP模型。

為了獲得負荷轉移率曲線，可以對實行區域的用戶做大量的調查，并收集以往尖峰電價實施前后相似日的負荷數據。根據用戶調查數據和負荷數據進行各時段負荷轉移率曲線的擬合。

根據該方法，可以得出其他5種負荷轉移率曲線與其線性分段函數，分別表示為尖-峰λjf、尖-平λjp、峰-平λfp、峰-谷λfg、平-谷λpg。根據擬合出的負荷轉移率曲線，可以將執行CPP之后的負荷響應模型表示為如式（4）。

式中：Tj，Tf，Tp，Tg分別代表不同時段；Lk0，Lk分別為CPP執行前后k時段的負荷；Lj，Lf，Lp，Lg分別為執行前各個時段的負荷平均值；k表示任一時段。

3 尖峰電價優化模型

3.1 目標函數

本文從2方面確立目標函數。在經濟方面，可以增加供電方的利潤，同時減少用電方的購電費用，減少了電力公司的投資成本。在電力配置方面，能夠更好有效地利用現有配置，提高整個系統的負荷利用率、運轉效率和穩定性[11-12]。

首先，盡可能減小尖峰負荷。在減小尖峰負荷的同時，也要避免峰谷顛倒。因此目標函數之一為最小化執行CPP后的最大負荷：

式中：Lk為執行CPP之后k時刻的負荷；Lmax為執行尖峰電價后的最大負荷。

另一個優化目標為最小化峰谷差，即使執行CPP之后的峰谷差最小化：

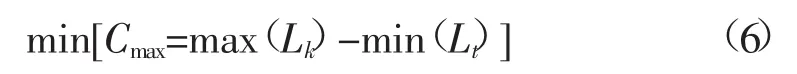
式中：Cmax為執行CPP后的最大峰谷差。

由于數學模型有2個目標函數，會一定程度增加計算的難度。為了降低計算難度同時保證結果精度，本文將2個目標函數可以轉化成1個目標函數min（αLmax+βCmax）。其中，α，β為2個目標函數的所占的權重。

3.2 約束條件

1）實施方與用戶方達到收入支出平衡：在執行CPP前后，實施方的收入不能降低；執行CPP后，用戶的購電費用不能有所增加。

式中：M0為執行CPP之前供電方所獲得的總額；M為執行之后供電方的收入。所以，第一個約束條件為M=M0。

2）用電總量不變：執行CPP后，要使用電量基本保持不變或者略有增加。

式中：Q0，Q分別為執行尖峰電價前、后的用電總量。

3）尖峰電價不能一味的升高，必須采取相應的政策將其控制在一定的范圍內。

式中：Pf為高峰電價；Pj為尖峰電價。

經過上述分析可知，求解該模型的關鍵步驟是建立正確目標函數與約束條件，在計算方法中，重點是變換多目標函數。

4 算例

本文以一企業的典型日負荷數據和負荷曲線進行分析，計算負荷轉移率，從而得到基于消費者心理學理論所建立的負荷模型。該模型的相關參數見表1。

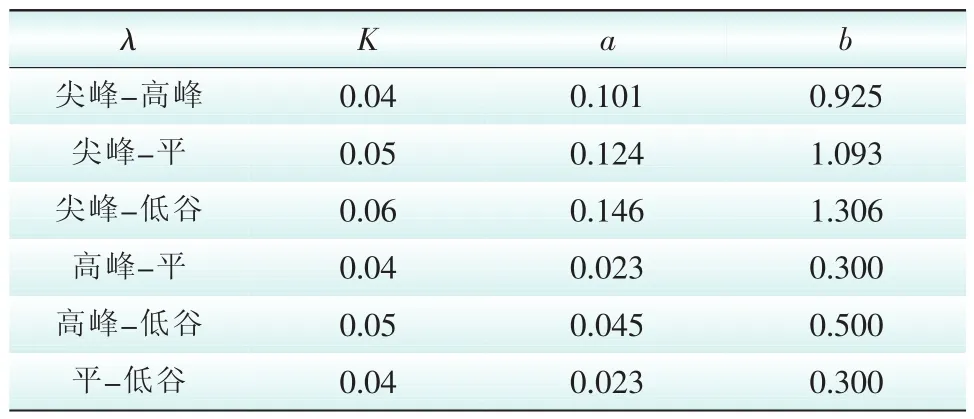
表1 CPP作用機理模型參數Tab.1 Parameters of the CPP mechanism model

將兩權重α和β假設等于0.5，原來的分時電價也已給出：

然后通過模糊隸屬函數法劃分時段，將24個小時分為4個時段：

與執行尖峰電價機制后作對比，經過計算尖峰電價為1.215元/kW·h，最低負荷為186.23 kW，最高負荷為317.57 kW。最大峰谷差降低為131.27kW，減少了55.23 kW，即29.727%；并且執行方的收入總額增加了4 811.30元，即0.001 981%，可以認為沒什么變化，滿足了所有的約束條件。執行CPP前后曲線的對比如圖4所示。

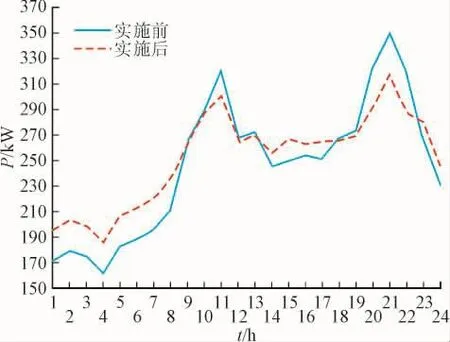
圖4 實施前后負荷曲線對照圖Fig.4 Comparison of load curves before and after implementation

圖4對照圖的曲線清晰可見，執行CPP之后的曲線明顯改善，最高點降低的同時，最低點也有所升高，致使峰谷負荷差異減少，目標函數達成。另外，從算例的計算結果中可以看出，執行CPP之后，購電費用與供電發的收入總額依舊保持原有的平衡，可以增強人們對CPP的積極性。在用電高峰期削減用電量可以降低電力消耗、緩解電力行業高峰期供電壓力，從而使現有發電設備得到有效利用，降低投資成本，甚至可以提高經濟與整個系統的穩定性。

5 結語

為了更好地體現出用戶對電價的承受能力，本文從消費者心理出發，建立的CPP模型更接近實際情況，考慮了用戶對電價的反應有一定的可行范圍。算例結果表明：執行CPP后，最大負荷減小，最小負荷增大，峰谷差縮小，負荷曲線變得相對平滑，發電站供電條件得到改善。同時，避免了給購電市場所帶來的危害，使購電與售電達到較好的支出收入平衡，且總用電量不減，實現了削峰填谷效應。

[1]張炳建，徐杰彥.中國電力需求響應的發展動因與實施手段[J].電力需求側管理，2013，5（4）：1-5.ZHANG Bingjian，XU Jieyan.Development motivation and implementation means of China’s electric power demand response[J].Power Demand Side Management，2013，5（4）：1-5.

[2]曾鳴.電力需求側響應原理及其在電力市場中的應用[M].北京：中國電力出版社，2011.

[3]李揚.考慮需求響應的尖峰電價實施效益的分析[J].電力需求側管理，2009，11（2）：12-14.LI Yang.An analysis of the effectiveness of the peak electricity price considering the demand response[J].Power DemandSideManagement，2009，11（2）：12-14.

[4]白蓉.用戶需求響應行為的建模分析[J].中原工學院學報，2016，27（3）：34-37.BAI Rong.Modeling and analysis of user demand response behavior[J].Journal of Zhongyuan University of Technology，2016，27（3）：34-37.

[5]劉繼東，韓學山.分時電價下用戶響應行為的模型與算法[J].電網技術，2013，37（10）：2973-2978.LIU Jidong，HAN Xueshan.The model and algorithm of the user response behavior of the sub time electricity price[J].Power System Technology.2013，37（10）：2973-2978.

[6]崔強，王秀麗，曾平良.調峰約束下考慮風電消納的多目標尖峰電價決策模型 [J].中國電機工程學報，2015，35（11）：2662-2669.CUI Qiang，WANG Xiuli，ZENG Pingliang.The multiobjectivedecisionmodelofwindpowerelectricitypricespikes considering peak constraint[J].Chinese Journalof Electrical Engineering，2015，35（11）：2662-2669.

[7]阮文駿，王蓓蓓，李揚.峰谷分時電價下的用戶響應行為研究[J].電網技術.2012，36（7）：86-93.RUAN Wenjun，WANG Beibei，LI Yang.Research on the user response behavior of peak and valley time price[J].Power Grid Technology，2012，36（7）：86-93.

[8]程瑜，霍娜娜.基于用戶響應的分時時段劃分[J].電力系統自動化.2012，36（9）：42-46.CHENG Yu，HUO Nana.Based on the user response time division[J].Power System Automation，2012，36（9）：42-46.

[9]張欽，王錫凡，王建學.尖峰電價決策模型分析[J].電力系統自動化，2008，32（9）：11-15.ZHANG Qin，WANG Xifan，WANG Jianxue.Analysis of peak electricity price decision model[J].Automation of Electric Power Systems，2008，32（9）：11-15.

[10]梁甜甜，王磊，高賜威.基于用戶響應的尖峰電價模型研究[J].華東電力，2013，41（1）：41-46.LIANG Tiantian，WANG Lei，GAO Ciwei.Research on peak electricity price modelbaseonuser response[J]East China Electric Power 2013，41（1）：41-46.

[11]楊娟.完善峰谷電價與尖峰電價機制緩解電力供求矛盾[J].中國物價.2012，32（5）：23-27.YANG Juan.Perfect peak and valley price and peak price mechanism to ease the contradiction between power supply and demand[J].China Price，2012，32（5）：23-27.

[12]周博，王博，高松.基于用戶響應的分時電價研究[J].智能電網.2016（3）：4（3）：307-311.ZHOU Bo，WANG Bo，GAO Song.Research on time sharing price based on user response[J].Smart grid，2016（3）：4（3）：307-311.

Peak Electricity Pricing Model Based on the Theory of Consumer Psychology

JI Lu1，ZHANG Kaoshe1，ZHANG Gang1，WANG Yongqing2
（1.Xi’an University of Technology，Xi’an 710048，Shaanxi，China；2.State Grid Shaanxi Electric Power Company Research Institute，Xi’an 710100，Shaanxi，China）

On the basis of the time-of-use pricing，this paper presents a critical peak pricing model（CPP）based on the consumer psychology theory.The fuzzy membership function is used to divide the time period of the daily load curve，and the CPP mechanism model is established according to the consumer psychology theory.Furthermore，the model is used to measure the response of the CPP to the CPP.The results show that CPP can effectively perform peak shaving and valley filling，improve the daily load curve，and solve the problem of dead and saturation zones of the user’s response to electricity price.

peak electricity pricing;demand response;user response;fuzzy membership function

在峰谷電價的基礎上，提出了一種基于消費者心理學理論的尖峰電價（Critical Peak Pricing，CPP）模型。通過模糊隸屬函數對典型日負荷曲線進行尖峰時段劃分，并且依據消費者心理分析建立用戶響應度曲線。以最小化峰谷差為目標函數建立尖峰電價作用機理模型，以用戶響應度量化用戶對CPP的響應，從而進行尖峰電價求解。算例表明，CPP可有效地進行削峰填谷、節約資源，改善日負荷曲線，可解決用戶對電價響應的死區與飽和區問題。

尖峰電價；需求響應；用戶響應；模糊隸屬函數

1674-3814（2017）09-0089-04

F407.61

A

國家自然科學基金（51507141）。

Project Supported by the National Natural Science Foundation of China（51507141）.

2016-11-22。

季 露（1990—），女，碩士研究生，研究方向為電力系統的測量、保護與控制；

張靠社（1965—），男，博士，副教授，從事電力系統分析方面的研究與教學工作。

（編輯 李沈）