K-均值聚類分析法在目標威脅評估中的合理性檢驗?

楊 聰 夏學成 黎鐵冰 黃傲林

（海軍工程大學 武漢 430033）

K-均值聚類分析法在目標威脅評估中的合理性檢驗?

楊 聰 夏學成 黎鐵冰 黃傲林

（海軍工程大學 武漢 430033）

結合現代防空作戰的特點，為了對空中目標進行合理的威脅評估，論文提出了基于K-均值聚類分析法的目標威脅評估的方法，并結合層次分析法對K-均值聚類分析法評估的合理性進行判斷，充分利用客觀和主觀相結合的方法，提高了評估方法的可信度，克服了單一評估方法的缺陷。論文首先對K-均值聚類分析法的原理和基本步驟進行了闡述，再針對評估結果的不足提出了層次分析法的排序模型，結合排序對聚類結果進行分析，使評估更加趨于合理性。

K-均值聚類分析法；層次分析法；威脅評估

1 引言

全方位、多批次的飽和攻擊是現今空襲的主要特點，并且空襲環境日益復雜，目標類型日趨多樣化，甚至有時還伴隨著誘騙和干擾的出現，但是在現代防空作戰中防空一方往往處境被動、兵力有限，難以有條不紊地對所有來襲目標作出較為合理的決策，對來襲目標進行有效抗擊和最大程度減少己方傷亡，因此目標威脅的合理評估成為了影響戰局的關鍵因素。

威脅評估是通過某種算法來估量來襲目標是否對我方某個陣地或單位構成威脅，并按照威脅程度的高低對目標進行排序，以此來判斷威脅程度的高低。敵目標威脅水平的高低受到客觀和主觀因素的影響，所以在威脅評估時要綜合目標多屬性的參數，才能較為精確地對來襲目標進行威脅度的估量。本文結合K-均值聚類分析法評估了來襲目標的威脅度，并且利用層次分析法對K-均值聚類法的評估模型作出合理性判斷，提高了威脅評估的準確性和合理度。

2 K-均值聚類分析法的原理

在聚類分析法中最常用的是K-均值聚類法，其基本方法是把樣品按最小化誤差函數為準則并聚集在預先設定的K個類的集合中［1］。

2.1 K-均值聚類分析法的步驟

在聚類算法中，結合防空作戰需求，目標的相似程度通常是用目標之間的距離來描述，距離越小則認為相似度越大，則聚為同一類的概率也越大，常用歐氏距離作為K-均值聚類算法中相似性度量的準則［2］。兩目標間的歐氏距離可以定義為對于有n個屬性的目標，若用xij描述第i個目標的第j個屬性，dij描述第i個目標到第j個目標間的距離，則

運用K-均值聚類法建模，大體上可分為下面三個步驟：

1）先設定聚類個數K，把目標粗略地劃分成K個類別。

2）對分類后的目標進行判別，將每個目標分到距離最近的一類中，并重新計算各類目標的均值。

3）通過重復2）的過程，直到各類無樣品元素的進出。

將樣本空間C={x1，x1，L，xi，Lxn} 的樣本分成K類，聚類中心為C={c1，c2，…，cj，…，ck} ，樣本空間內所有樣本點與所屬聚類均值距離的總和用函數D表示，其數學表達式為

目標函數D可以表現出聚類分析結果的特征，其值越小，則表示該類別中越相關、越獨立。將歐氏距離代入上式，可得

2.2 K-均值聚類分析法的不足

K-均值算法理論嚴密，實現快速簡單，并且在數據處理中時間復雜度低，聚類時間相對較短，可以較好地應用在防空作戰體系中。但聚類中心均值的選取決定了該算法結果是否準確，而且會對結果產生較大差異，并且若中心均值的選取不合適，則有可能會把原本屬于同類的目標分到不同類別中，也有可能出現對同一個目標重復分類的情況，導致分類不夠準確［3］。

為了對K-均值聚類分析法在目標威脅評估的合理性進行檢驗，我們在進行評估的基礎上，利用層次分析法對分類后得到的模型進行威脅度等級的排序，對目標的評估進行主觀的綜合評價，獲取更高的準確度。

3 層次分析法的基本原理

層次分析法是在一個系統內進行目標問題的決策，將系統分為若干個層次結構，求出各層次中目標屬性的權重并進行總排序，得到目標優化決策的系統方案［4］。

運用層次分析法建模，大體上可分為四個步驟［5］：

1）根據決策關系建立合適的層次結構模型，明確所要考慮的目標各個屬性之間的關系。

2）構造出各層次的成對比較判斷矩陣。

3）由判斷矩陣計算類別的相對權重。

4）依據各層權重向量得到總的合成權重，對目標按照權重值進行威脅度排序。

3.1 層次結構的確立

針對防空作戰的實際情況，首先建立層次結構模型，將組成系統的元素分組形成互不相交的自上而下逐層支配的層次，一般可分為三類：最高層、中間層、最底層。

3.2 成對構造矩陣的構造

對目標各屬性分別兩兩對比其相對重要性，按照9標度法構造成對比較判斷矩陣［6］。

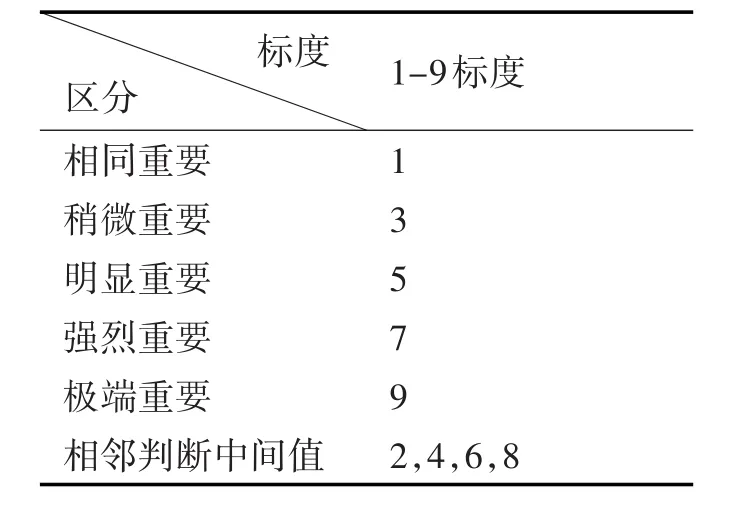
表1 9標度準則

設Aij是按照9標度準則進行構造時，屬性i相對于屬性j的重要性，則成對比較矩陣為A=(aij)n×n。

3.3 單層元素相對權重的計算

3.4 一致性檢驗

1）計算一致性指標C.I

2）查找相應n的平均隨機一致性指標R.I［7］

3）計算一致性比例

當CR＜0.1時，即可認為比較矩陣通過了一致性檢驗，若計算出CR≥0.1時，則應對比較矩陣作合適的修正，以確保一定程度下的一致性。

3.5 計算總合成權重并排序

將矩陣的特征向量加權后就可以得到總的權重系數，接著計算出層次總排序向量，從中按照數值從大至小對目標威脅度進行排序［8～9］。

層次分析法使復雜的系統分解，把對多目標多屬性的問題相對簡化，通過兩兩比較確定較上一層次的權重后得到排序結果，而且更加注重對決策問題作出定性的分析和判斷。

4 結果相似程度的比較

防空作戰決策人員可根據排序情況對來襲目標進行威脅等級劃分，將排序結果與K-均值聚類法進行比較，考慮兩種排序結果的特征，比較同一類的目標威脅程度是否相近，則可判斷用K-均值聚類分析法得出的結果是否合理，也可作為聚類分析法的一種補充。

5 應用實例

在實際的防空作戰中，假設要進行威脅評估的目標已經過類型識別，可根據不同的因素特征分為不同的類別。本例模擬來襲每一批次有7個目標，考慮目標的5個屬性，分別為目標類型、速度、航向角、干擾能力和距離。

首先將7個來襲目標的屬性進行量化，下面是一個量化方案［9］，具體見表2、表3。

按目標類型分為轟炸機、武裝直升機、無人偵察機、空地導彈、彈道導彈，依次量化為5、3、2、7、9；

按 速 度（ v ，m/s）量 化 ，v≥2000為9，2000＜v≤1500為8 ，1500＜v≤1200為7 ，1200＜v≤1000為6 ，1000＜v≤800為5 ，800＜v≤600為4 ，600＜v≤400為3，400＜v≤200為2，v＜200為1；

按目標航向角（α，°）量化，0°＜α≤5°為9 ，5°＜α≤15°為8 ，15°＜α≤30°為7 ，30°＜α≤60°為6 ，60°＜α≤90°為5 ，90°＜α≤120°為4 ，120°＜α≤180°為3，180°＜α≤270°為2，270°＜α≤360°為1；

按 距 離（d，km）量 化 ， d＜50為9 ，50＜d≤100為7 ，50＜d≤100為7 ，100＜d≤200為5，200＜d≤300為3，d＞300為1；

按抗干擾能力量化，抗干擾能力強、中、弱、無依次量化為9、6、3、1。

采用聚類分析法對來襲目標進行聚類分析，先確定聚類數目K=3，經過Matlab編程計算后，可得到聚類結果，目標1和目標4為類別1，目標2、3、5、6為類別2，目標7為類別3，較好地對來襲目標分類，并且得出目標威脅度從大到小為類別1，類別2，類別3。

下面利用層次分析法對目標威脅程度進行排序［11～12］。

1）根據考慮來襲目標的屬性建立層次結構模型，如圖1。

表2 目標屬性值

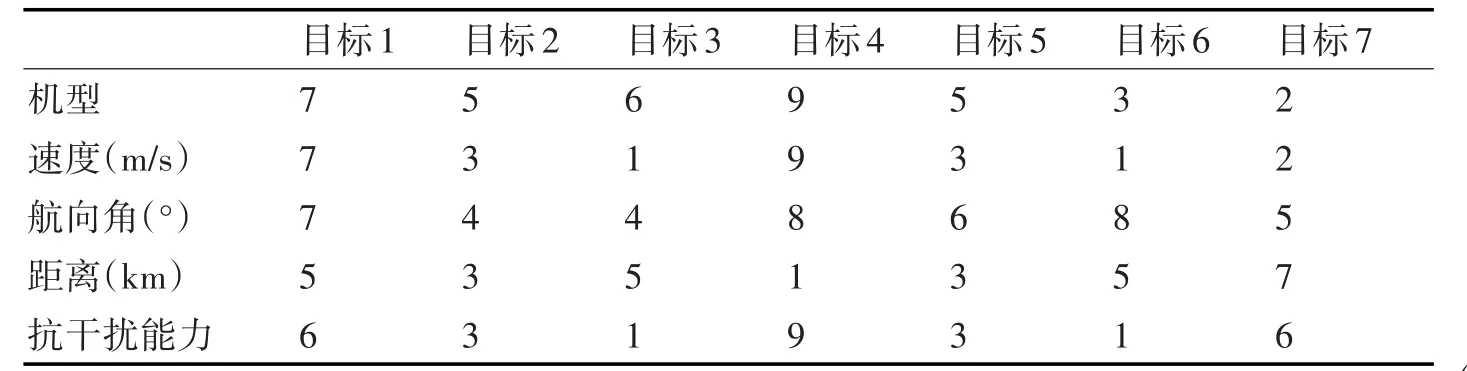
表3 目標屬性量化值

2）構造成對比較矩陣。

首先對來襲目標的屬性按照9標度法進行量化處理，通過專家知識系統建立判斷矩陣，求出單目標層次矩陣的特征向量ω=[0.4711 0.2638 0.1431 0.0781 0.0440]T，最大特征值為λ=5.0294，則=0.0074。max查表得 R.I=1.26，計算=0.0066＜0.1，故單目標成對比較矩陣符合一致性檢驗的要求。

遵循上述方式依次計算出各層屬性的特征向量，得到合成權重為：*ω =[0.19230.1230 0.0362 0.3108 0.1534 0.0412 0.0017]T即各目標的排序為。

結合層次分析法的排序模型，分析后可得同一類別中的目標排序結果臨近，聚類分析法得到的結論正確，進行威脅排序時沒有出現把原本屬于一類的目標拆分到不同類別中的情況，檢驗出聚類分析法在對目標威脅度的評估模型里較為合理。

6 結語

本文以防空作戰為背景，提出了基于K-均值聚類分析的威脅評估方法，再利用層次分析法對聚類后的類別進行合理性檢驗，在客觀評價的基礎上結合了專家經驗，把定性分析與定量分析相結合進行目標綜合決策，很大程度上提升了評估的可信度和準確度，適用于實時、快速的防空作戰體系。本文下一步對聚類數目將進一步明確及優化，從而提高對目標的聚類效果。

［1］任青山，方逵.K-means聚類算法的一種改進方法［J］.福建電腦，2016（5）：1-3.

［2］何曉群.多元統計分析（第三版）［M］.北京：中國人民大學出版社，2012：36-45.

［3］馮波，郝文寧，陳剛，占棟輝.K-means算法初始聚類中心選擇的優化［J］.計算機工程與應用，2013（14）：182-185.

［4］張善文，劉進忙.以目標類型為主的一種威脅評估方法［J］.系統仿真學報，2002，14（8）：1109-1111.

［5］閆沖沖，郝永生.基于層次分析法（AHP）的空中目標威脅度估計［J］.計算技術與自動化，2011，30（2）：118-121.

［6］唐雪松，郭立紅，陳長喜.基于AHP的威脅評估與排序模型研究［J］.微計算機信息，2006，22（9）：35-38.

［7］魏世孝，周獻中.多屬性決策理論方法及其在C3I系統中的應用［M］.北京：國防工業出版社，1998：161-166.

［8］徐品高.空中目標威脅值的評定［J］.戰術導彈技術，2000（2）：1-8.

［9］徐品高.特種空中目標威脅值的評定［J］.戰術導彈技術，2000（2）：14-19.

［10］王百合，黃建國，張群飛.基于層次分析法的水下多目標威脅評估模型［J］.艦船科學技術，2006，28（6）：75-77.

［11］馮璐，高曉光.層次分析法在多目標攻擊邏輯與決策中的應用［J］.西北工業大學學報，1999，17（4）：515-519.

［12］熊銳，蔣曉亞.層次分析法在多目標決策中的應用［J］.南京航空航天大學學報，1994，26（2）：283-288.

Analysis of Rationality of K-means Cluster Analysis In Target Threat Assessment

YANG Cong XIA XuechengLI TiebingHUANG Aolin
（Naval University of Engineering，Wuhan 430033）

Combining with the characteristics of modern air defense combat，in order to carry on the reasonable threat assess?ment on air targets，K-means clustering are proposed in this paper based on the analysis of target threat assessment method.At the same time，this article uses analytic hierarchy process（AHP）to evaluate the rationality of K-means clustering analysis’s judgment and makes full use of the combination of objective and subjective method to improve the credibility of the evaluation method.First?ly，this article narrates the principles and basic steps of K-means clustering analysis，then puts forward the sorting model of AHP aiming at the shortcomings of the evaluation results.Finally，the clustering results are analyzed by combining the sorting results，which makes the evaluation tend to be more reasonable.

K-means cluster analysis，AHP，threat assessment

TP301.6

10.3969/j.issn.1672-9730.2017.11.006

Class Number TP301.6

2017年5月4日，

2017年6月26日

楊聰，男，研究方向：電子對抗。夏學成，男，研究方向：電子對抗。黎鐵冰，男，博士研究生，工程師，研究方向：信息作戰保障。黃傲林，男，博士研究生，工程師，研究方向：信息作戰保障。