氣液兩相流管道泄漏瞬態模型及數值計算

蔡永橋，盧 進，王 慶，孫曉陽，曹學文

1.中海油能源發展裝備技術有限公司，天津 300459

2.中海油山東化學工程有限責任公司，山東濟南 250014

3.中國石油大學（華東）儲運與建筑工程學院，山東青島 266580

氣液兩相流管道泄漏瞬態模型及數值計算

蔡永橋1，盧 進1，王 慶2，孫曉陽3，曹學文3

1.中海油能源發展裝備技術有限公司，天津 300459

2.中海油山東化學工程有限責任公司，山東濟南 250014

3.中國石油大學（華東）儲運與建筑工程學院，山東青島 266580

氣液兩相流管道一旦有泄漏發生，管道壓力、截面含液率及流速等參數均會發生改變，分析泄漏過程中氣液兩相流的瞬態變化對于探究管道泄漏特征、實施兩相流管道泄漏檢測與定位具有重要意義。對氣液兩相流泄漏過程進行瞬態分析，在雙流體模型的基礎上建立氣液兩相流泄漏系統數學模型，利用隱式差分法求解控制方程，并用C++編程計算氣液兩相流泄漏數值解，分析分層流條件下泄漏對管道壓力、截面含液率、氣液相流速等參數的影響，將數值計算結果與氣液兩相流泄漏實驗數據進行對比。結果表明：管道泄漏后，泄漏點下游管道壓力、截面含液率、氣液相流速等參數值均下降，且數值計算結果與實驗數據趨勢一致，證明所建立的泄漏模型適用性較好。

氣液兩相流；分層流；泄漏模型；數值計算；實驗研究

油氣混輸管道作為一種高效、安全、經濟、環保的運輸手段，在石油、天然氣等能源運輸中發揮著重要的作用。到目前為止，油氣多相流混輸管道已成為國內外海底管道的主要運輸方式。管道泄漏問題一直是管道安全生產維護領域的難題，且事故發生率較高，老化、腐蝕、磨損、焊接缺陷、設計缺陷、運行超過設計極限及故意破壞等多種原因，都會導致管道的泄漏，進而造成嚴重的后果[1-2]。在油氣混輸管道的運行管理中，及時檢測到管道泄漏并定位，是管道安全運行的必要前提[3]。氣液兩相流管道流型多，流動參數之間的關系復雜，一旦有泄漏發生，其壓力、持液率、介質流速等參數值發生改變，影響泄漏檢測的精度及靈敏度。因此建立氣液兩相流泄漏系統數學模型，分析泄漏過程中氣液兩相流的瞬態變化，對于探究管道泄漏特征、實施兩相流管道泄漏檢測與定位具有重要意義。

本文在雙流體模型的連續性方程和動量方程的基礎上引入泄漏方程，并結合分層流的結構方程，建立分層流條件下氣液兩相流泄漏系統數學模型，并利用隱式差分法對模型進行求解，給出水平管道氣液兩相分層流動穩態及泄漏工況的計算方法。利用C++編程求解分層流泄漏偏微分方程組，得到管道泄漏后壓力、持液率等流動參數的變化規律，為氣液兩相流管道泄漏研究提供參考。

1 模型建立

1.1 假設條件

管道作為一個水力系統，沿線任一點發生泄漏都會引起該點流動參數的變化，破壞管道的流動狀態，該瞬變波動從泄漏點沿管道向上下游傳播，使整條管道進入瞬變流動狀態[4]。在氣液兩相雙流體模型的基礎上，以流體力學基本守恒方程為基礎，引入泄漏方程，并結合氣液分層流的結構計算式，建立氣液分層流泄漏瞬態方程組[5-9]。針對分層流管道輸送的特點以及前人所作的研究成果，提出如下假設[10]：

（1）管道內氣相介質為理想氣體。

（2）管道內氣液兩相處于熱力學平衡狀態，忽略相變與相間傳質。

（3）管道內介質流動過程中溫度保持不變，采用等溫一維模型，忽略能量方程。

（4）沿管道橫截面上，氣液兩相壓力、流速、密度等各流動參數在各相所占的平面內均勻分布。

1.2 數學模型

基于所作的假設，可以得到水平管路中氣液兩相流動的基本方程如下：

（1）連續性方程。

根據氣液介質各自的流量守恒關系，氣相和液相的連續性方程分別為：

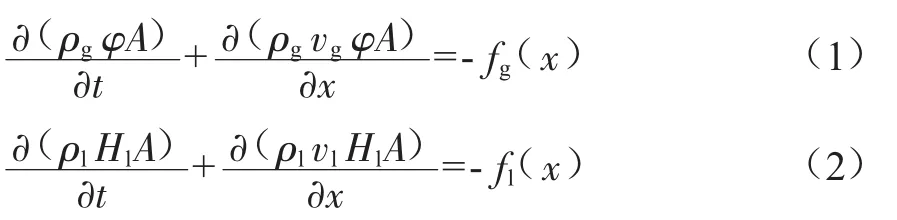
式中：ρg、ρl分別為氣、液相密度，kg/m3；φ為截面含氣率即氣相流通面積與管路總流通面積之比，%；Hl為截面含液率即液相流通面積與管路總流通面積之比，%；A為管道截面積，m2；t為時間，s；vg、vl分別為氣、液相速度，m/s；x為管道軸向坐標，m；fg（x）、fl（x）分別為x位置處的氣、液相泄漏質量，kg。

（2）動量守恒方程。

氣、液相動量守恒方程分別為：

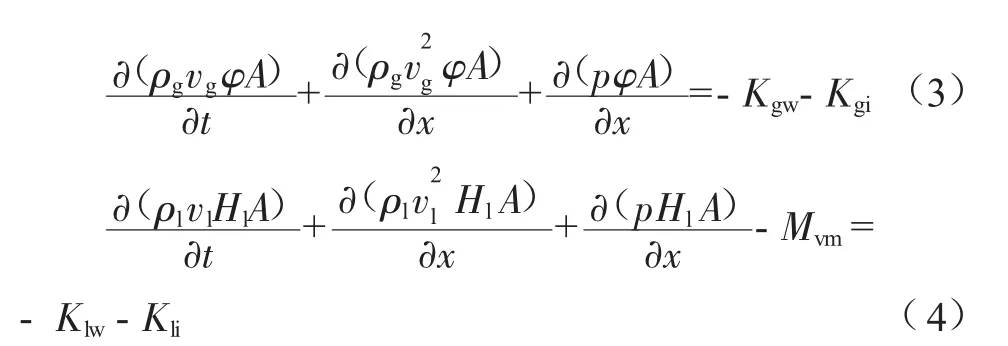
式中：p為管道內壓力值，MPa；Kgw、Klw分別為單位長度氣、液相與管壁間的剪切力，N/m；Kgi、Kli分別為單位長度氣相側與液相側受到的相間剪切力，N/m；Mvm為單位長度相間虛擬質量力，N/m，分層流中通常為0。

（3）密度方程。

流體密度是壓力的函數，假定管道橫截面上氣液兩相壓力相同，p=pg=pl，由理想氣體狀態方程可知，氣相密度為：

式中：Z為氣體壓縮因子；R為氣體常數，J/（mol·K）；T為氣體溫度，K；cg為氣體中的聲速，m/s。

（4） 泄漏方程[11-12]。

參照節流噴嘴流量公式，以泄漏點處管內外壓差為基礎，引入泄漏參數Fk，從而計算泄漏混合介質質量。Fk為經驗常數，取值與泄漏尺寸、泄漏位置及持液率有關，應根據現場數據或實驗數值擬合取得。在此基礎上，引入狄克拉分布函數δ計算泄漏對于管道不同位置流體各參數的影響，有：

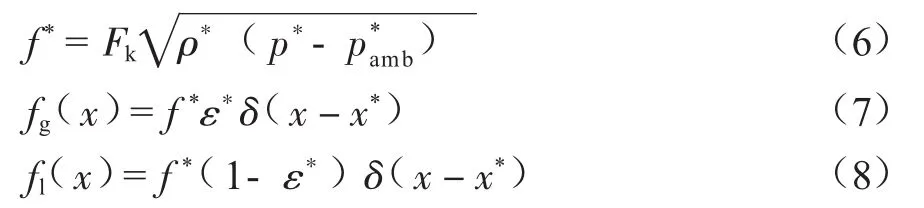
式中：f*為泄漏質量，kg；ρ*為泄漏點氣液混合物密度，kg/m3；p*為泄漏點處管道內壓力，MPa；pamb*為泄漏點處管道外壓力，架空管道則為大氣壓力，水下管道則為該水深處的靜水壓力，MPa；ε*為泄漏氣體的體積分數，%；x*為泄漏點位置，m。

δ為狄克拉分布，在除了零以外的點，其函數值等于零，而其在整個定義域上的積分等于1，用數學式表示為[13]：

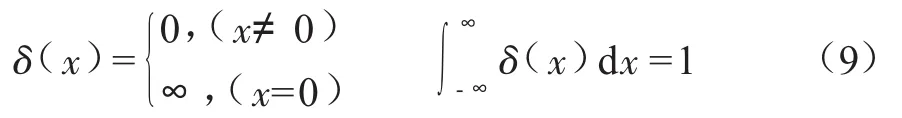
如果函數的非零值是在自變量為x*時取得的，可用變形的狄克拉分布表示管道上有一點發生泄漏，而管道其他位置完好。具體表示為：

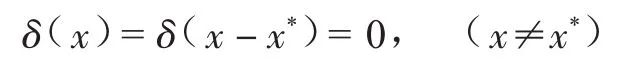
（5）分層流結構方程。

本文的研究對象為氣液分層流流動，分層流氣液相分布如圖1所示，在重力作用下，液相位于管道底部，氣相位于管道頂部，兩相之間有明顯的分界面，氣液界面采用FLAT模型[14]。

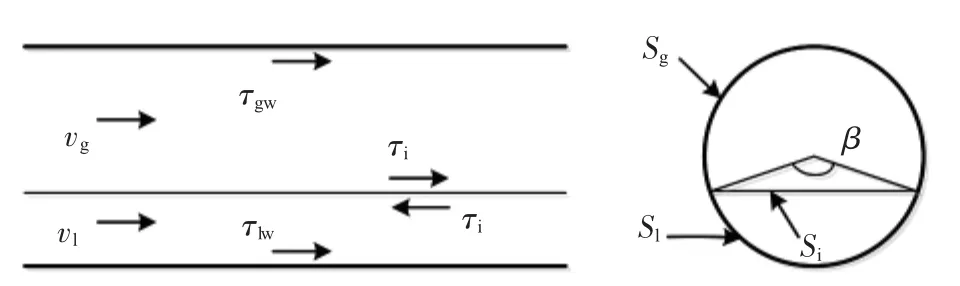
圖1 分層流氣液相分布

氣相與管壁間的剪切力為：

液相與管壁間的剪切力為：

相間剪切力：

式中各物理量的求解方法可參考文獻[14]。

以上建立起了分層流條件下氣液兩相管道泄漏瞬態分析方程組，結合管道泄漏相應的邊界條件，描述泄漏瞬變過程中各參數的變化情況。

1.3 方程求解

對管道處于正常運行和發生泄漏狀態分別進行求解，其邊界條件以實驗室環道參數條件為基礎，給定管道入口氣液流量及入口壓力，流體泄漏過程中泄漏點處背壓為恒定值，即外界大氣壓pamb。

采用隱式差分法對控制方程偏微分方程組進行求解。用網格化方法[15]處理變量管長x和時間t，管道差分網格如圖2所示，則由隱式差分法可以得到偏微分方程式（1）至式（4）的差分方程。

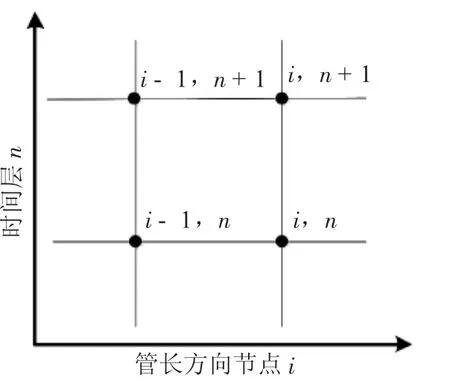
圖2 管道差分網格示意

氣體連續性方程離散為：

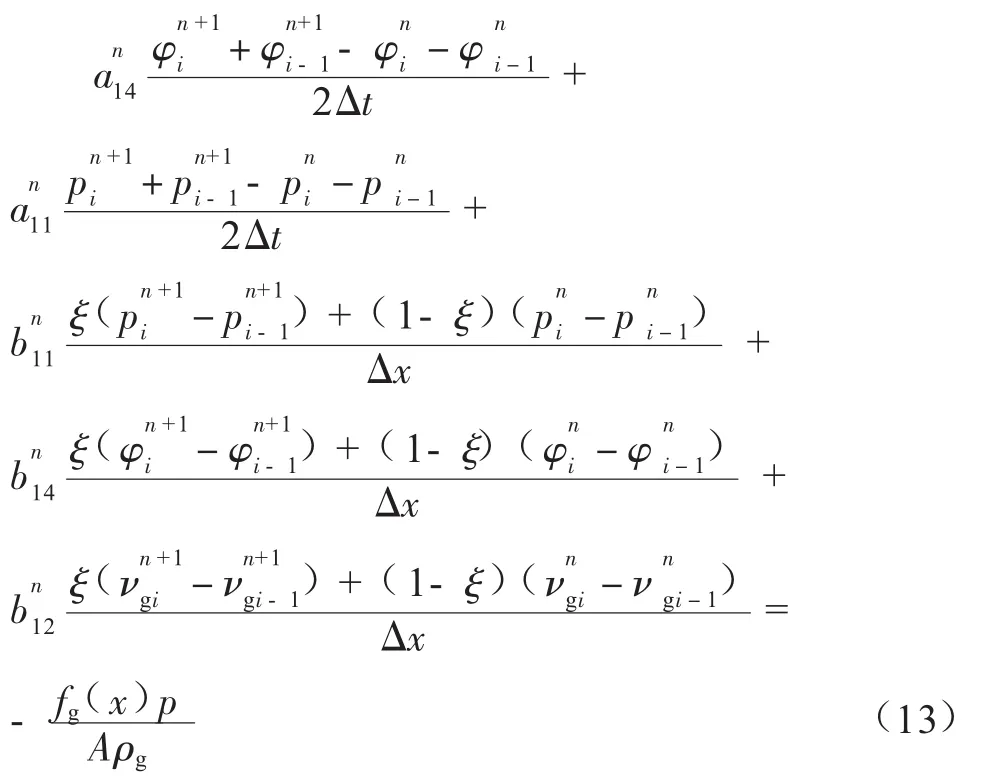
式中：ajk、bjk分別代表對t和x進行微分處理，其中下標j=1，2，3，4分別對應氣相連續性方程、液相連續性方程、氣相動量方程以及液相動量方程，下標k=1，2，3，4 分別對應參數p、φ、vg、vl；為（ i，n）節點處的截面含氣率，%；為（i，n） 節點處的壓力值，MPa；為（i，n） 節點處的氣相速度，m/s；ξ為加權系數；△t為時間步長，s；△x為距離步長，m。

同理，可分別寫出液相連續性方程及氣、液相動量方程的離散格式。

液相連續性方程：

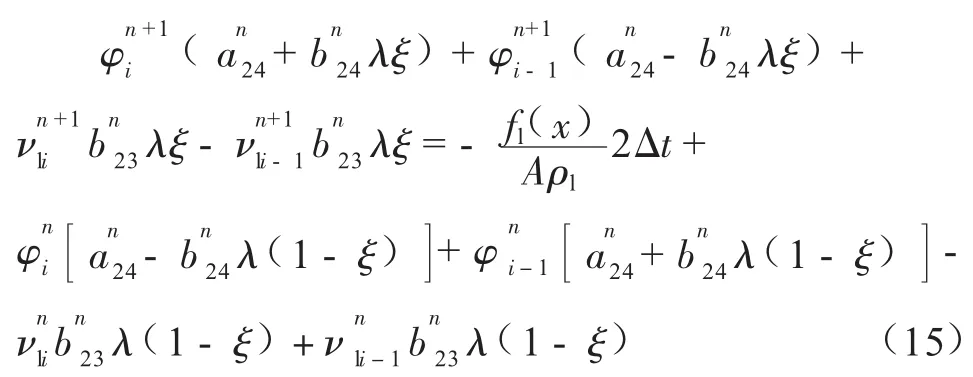
氣相動量方程：

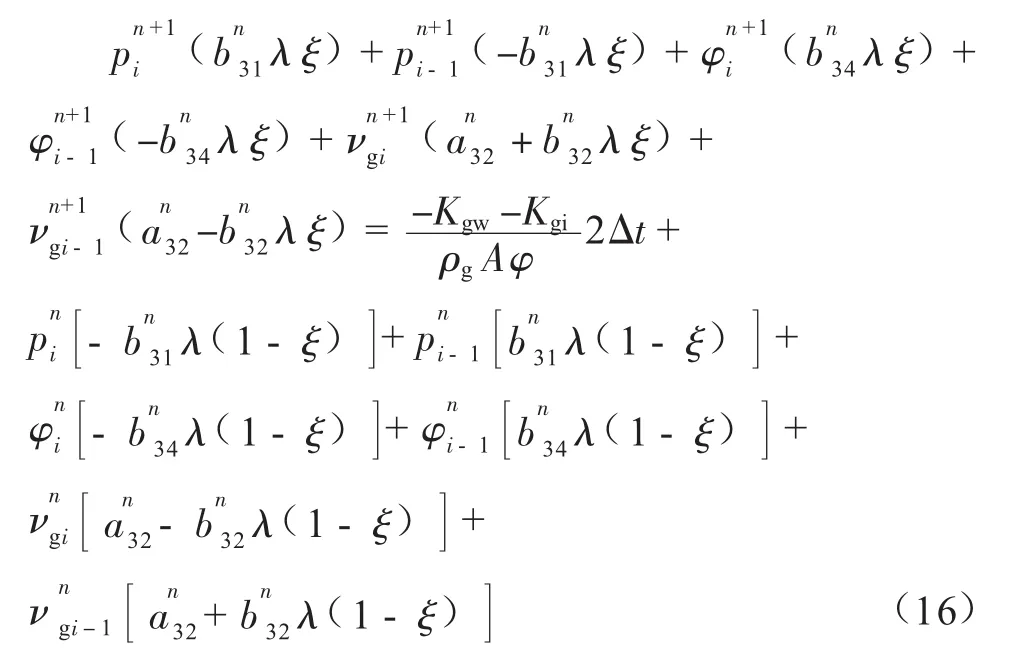
液相動量方程：

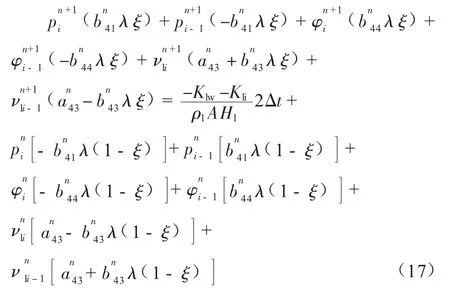
式（14）至式（17）為計算管道壓力、氣液相流速及含氣率的差分方程。瞬態方程的求解過程為：

（1）給定管道距離步長與時間步長。

（2）給定管道入口氣、液相流量及入口壓力值，求解管道穩定運行時各管段剖分面上的運行參數值。

（3）指定泄漏位置，將該位置管道壓力值代入式（6）計算泄漏量。

（4） 由0時間層的參數代入式（14）至式（17），求出初始時刻各流動參數值。

（5）重復步驟（3）～（4），直到時間層為指定時間。

2 計算結果

2.1 計算工況

以實驗室管道基礎數據為初始條件，利用C++進行編程計算。圖3為氣液兩相流實驗環道的流程示意圖，實驗介質為空氣和水，實驗環道采用不銹鋼管焊接而成，在環道的實驗段上有4段透明有機玻璃管，長約2 m，以便觀察多相流在管道中的流型。管道長40 m，分為DN50、DN80兩種管徑管段，管道入口處氣、液相流量分別為15.6 m3/h、0.9 m3/h，管道入口壓力為1.3 MPa。計算的距離步長與時間步長分別取0.5 m、0.1 s。根據實驗室環道情況，取泄漏點為距管道入口12 m處。

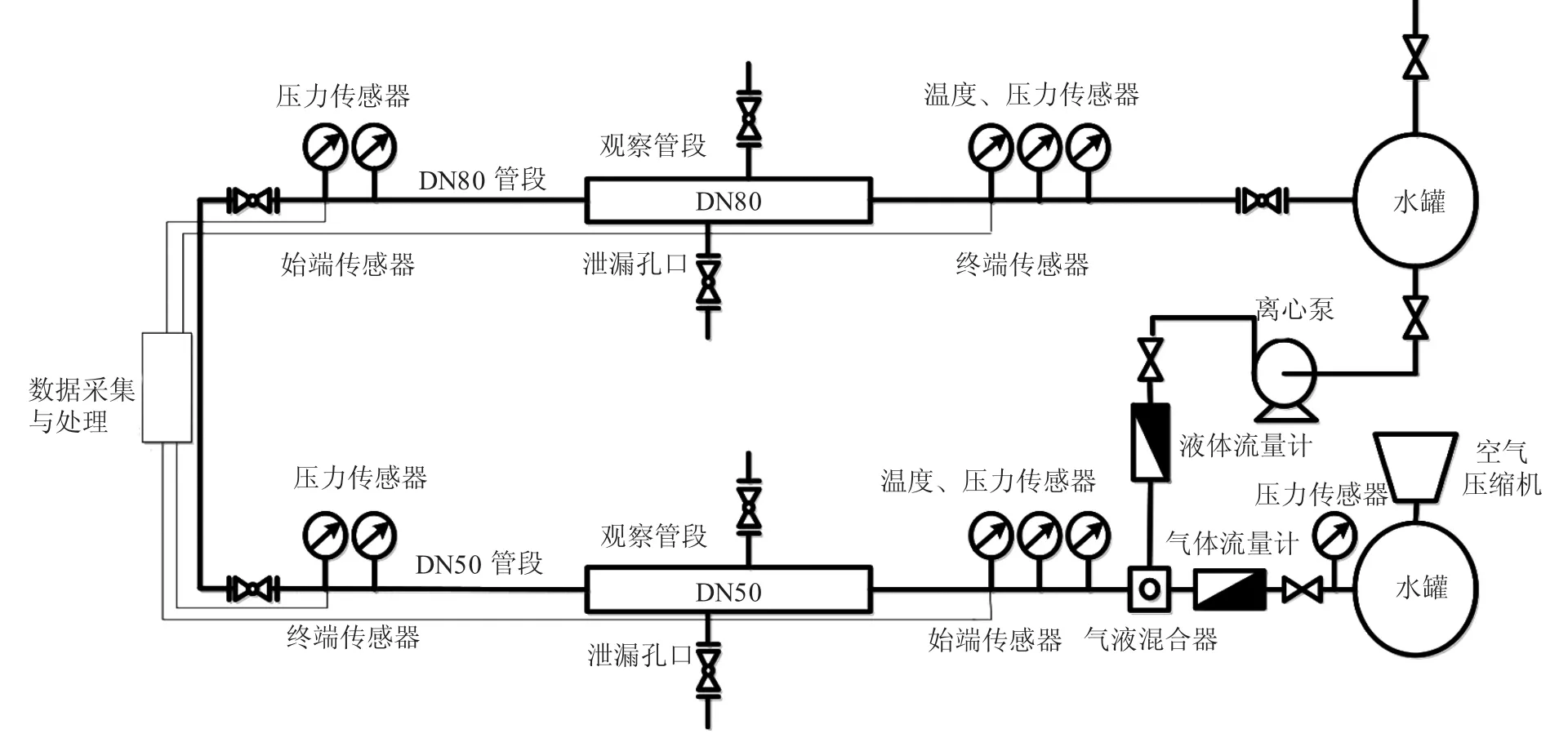
圖3 實驗環道示意

多相流實驗環道實物如圖4所示。多相流部分實驗裝置主要包括：氣液相介質供應系統、流量調節裝置、氣液相分離系統、實驗測試管段、儲液裝置以及控制系統；泄漏部分實驗裝置包括：信號采集傳感器、泄漏口模擬系統、信號采集與處理系統。環道沿程設置了溫度、壓力、流型等測量點，利用LabView編程采集實驗管路起點的氣液流量、溫度、管道沿線壓力。

圖4 多相流實驗環道實物照

沿程采用4個MPM480型壓力傳感器，量程0～400 kPa，精度為0.25%。壓力傳感器及泄漏點（DN80、DN50兩部分管段上分別各設置一處泄漏點）位置見表1。由于泄漏點的周向位置對于分層流的泄漏規律有很大影響，故將每個泄漏點又分為上泄漏口和下泄漏口。用球閥連接孔板法蘭的裝置模擬泄漏系統，快速打開球閥模擬管道發生泄漏，通過更換不同尺寸的孔板，調節泄漏孔口直徑。模擬泄漏系統實物及其結構如圖5所示。

表1 傳感器（P1～P4） 及漏點位置

2.2 管道參數變化

管道沿程壓力、持液率及氣、液相介質流速的數值仿真計算結果如下：

（1）管道沿程壓力的變化。由圖6可知，管道發生泄漏后，部分流體流出管道，引起管內流體局部密度減小，故泄漏點壓力迅速降低。在實驗室條件下，兩相流實驗環道入口壓力由壓縮機控制，故在數值模擬中，管道發生泄漏后泄漏點上游壓力幾乎無變化；而在實際事故中，這種壓力降低的趨勢應以壓力波的形式迅速向管道上下游傳遞，導致管道沿線壓力值均降低。管道壓力的變化僅在泄漏發生后2 s內變化明顯，之后管道維持在一個低于管道正常操作壓力的穩定壓力值運行。

（2）管道沿程截面含液率的變化。當管道發生泄漏，尤其是較小泄漏的情況，截面含液率的變化對泄漏檢測尤為重要。截面含液率的變化越大，造成的管道局部壓降就越大。Stuart等人[16]的研究表明，對于分層流的泄漏檢測依賴于對截面含液率的分析。由圖7可知，泄漏導致泄漏點處截面含液率迅速下降。截面含液率下降的趨勢僅對泄漏點下游產生影響，對管道上游幾乎無影響，沿程數值基本一致。這是由于在流體流型為分層流的條件下，位于管道底部的泄漏點導致管道泄漏的流體主要是液相，故截面含液率不斷降低。

圖5 漏點處實物照及其結構

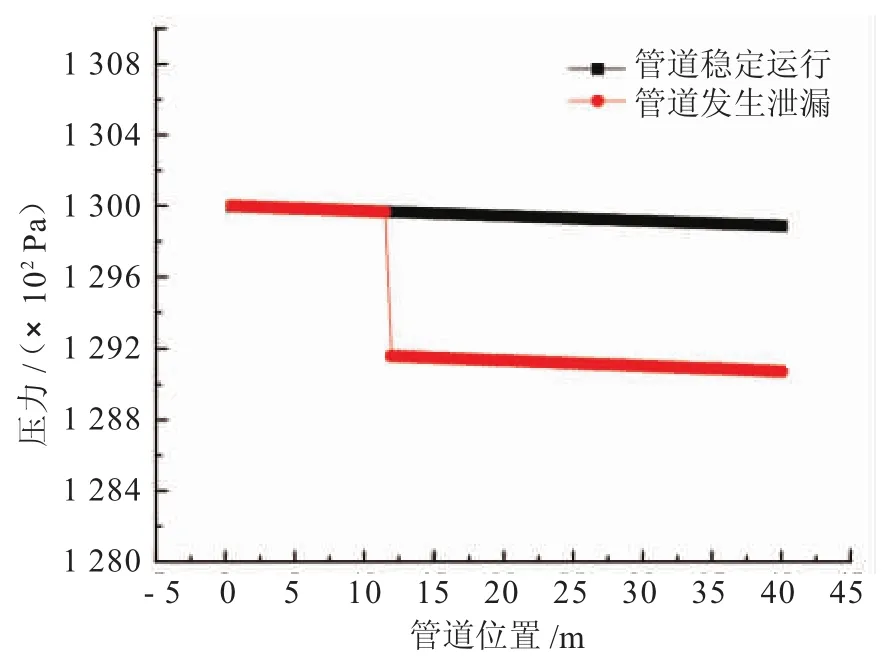
圖6 數值模擬管道穩定運行與泄漏后沿程壓力

（3）管道沿程氣相介質流速的變化。由圖8可知，管道發生泄漏后，管道下游氣體介質流速迅速降低。當管道正常運行時氣相的流速為2.207 m/s，泄漏發生瞬間泄漏點氣相流速降低至2.202 m/s。這是由于氣體在管道內的流速與管道壓力有關，泄漏后管道壓力降低，故氣體流速下降明顯。另外由于假設管道發生泄漏時泄漏點位于管道下部，流出的流體全部為液體，泄漏后管道持液率降低，氣相流通面積變大，進口流量恒定，故泄漏點下游氣相流速降低。由于管道入口處流量固定，所以泄漏點上游流速基本不變。

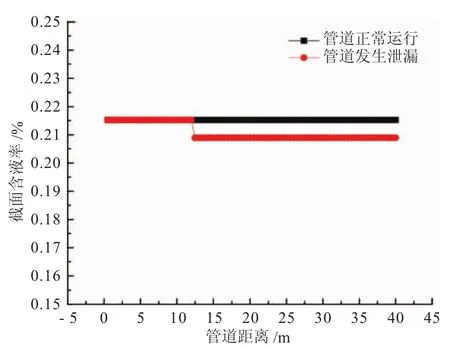
圖7 數值模擬管道穩定運行與泄漏后管道截面含液率變化

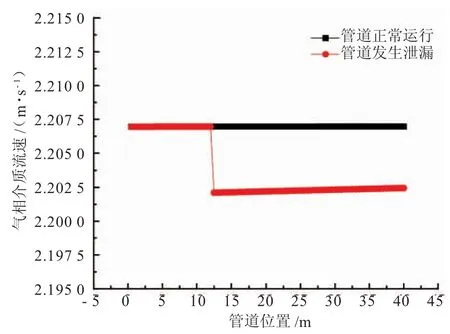
圖8 數值模擬管道穩定運行與泄漏后氣相流速變化

（4）管道沿程液相介質流速的變化。由圖9可知，管道正常運行時，管內為分層流流動，液體流速較低，為0.127 m/s；管道發生泄漏后，泄漏的介質全部為液體，管道下游液體介質流速迅速降低至0.122 m/s。

2.3 數值計算與實驗數據對比

管道發生泄漏后，管道末端壓力略有降低。將實驗采集到的管道出口壓力信號變化值與數值模擬計算壓力值進行對比，見圖10。由于實驗用壓力傳感器精度較差，故對實驗數據與數值計算數據均做了歸一化處理，將壓力值轉化為無量綱的壓力幅值數據，然后進行比較。

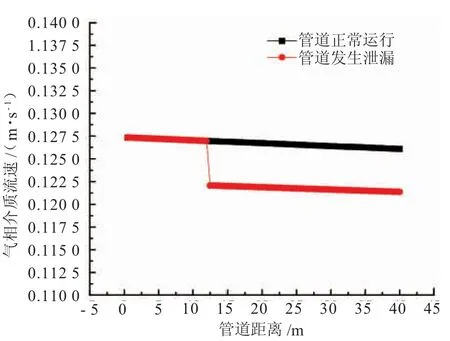
圖9 數值模擬管道穩定運行與泄漏后液相流速變化

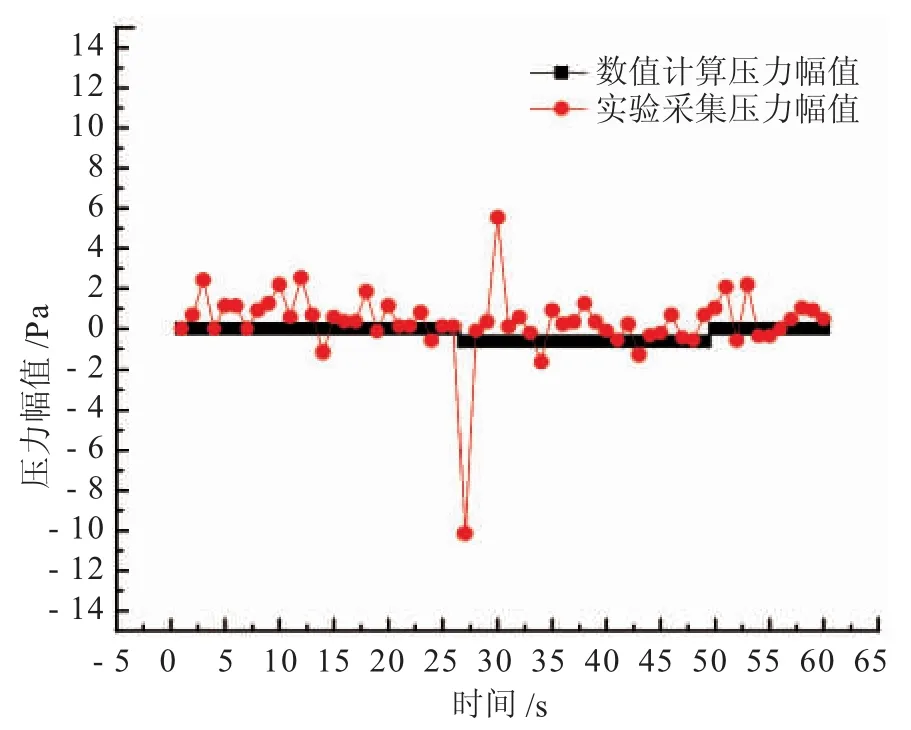
圖10 管道末端壓力幅值的數值模擬與實驗數據對比

從圖10中可以看出，數值計算結果與實驗數據變化趨勢吻合。實驗中，管道正常運行25 s后打開泄漏閥門，流體從管道下部泄漏孔流出，泄漏約20 s后關閉閥門，管道恢復正常運行。泄漏導致管道壓力迅速降低，上游介質流量補充導致壓力突降后迅速增大，之后在一個略低于正常運行時的壓力值上下波動。因實驗環道管道長度較短，且管內壓力較低，所以發生泄漏后，壓力減低不明顯，但從圖10中可以看出泄漏發生后壓力有下降的趨勢，停止泄漏后管道壓力恢復到正常值。

3 結論

（1）利用C++編程求解分層流泄漏偏微分方程組，得到管道泄漏后壓力、持液率等流動參數的變化規律，管道發生泄漏后，泄漏點下游壓力迅速降低，持液率迅速降低，氣、液相流速均降低；管道上游流動參數影響較小。

（2）數值模擬結果與實驗數據吻合較好，對比數值模擬結果與實驗數據可知，泄漏發生后管道末端壓力略有下降，停止泄漏后管道壓力恢復到正常值。

[1]吳世來.輸氣管道泄漏音波檢測信號處理的研究[D].沈陽：沈陽工業大學，2007.

[2]余洋.中國油氣管道發展現狀及前景展望[J].國際石油經濟，2007，15（3）：28-33.

[3]劉濤.管道檢測系統中的信號處理技術研究[D].天津：天津大學，2007.

[4]李玉星，馮叔初.濕天然氣管輸瞬變流模型及數值模擬技術研究[J].油氣儲運，1998，17（5）：11-17.

[5]韓煒.管道氣液兩相流動技術研究[D].成都：西南石油學院，2014.

[6]孔祥偉，林元華，何龍，等.一種考慮虛擬質量力的兩相壓力波速經驗模型[J].力學季刊，2015（4）：611-617.

[7]江延明，李玉星，馮叔初.氣液兩相流瞬變流數值模擬研究[J].油氣儲運，2005，24（11）：22-27.

[8]陳家瑯，陳濤平.石油氣液兩相管流[M].2版.北京：石油工業出版社，2010：17-20.

[9]李玉星，馮叔初.濕天然氣管輸瞬變流模型及數值模擬技術研究[J].油氣儲運，1998，17（5）：11-17.

[10]王文光，顏慧慧，曲兆光，等.起伏濕氣管路持液率和壓降計算模型[J].石油工程建設，2016，42（6）：1-4.

[11]BUENO D E G P，FIGUEIREDO A B，BAPTISTA R M，et al.Numerical simulation of stratified two-phase flow in a nearly gas-liquid pipeline with a leak[C]//Calgary：International Pipeline Conference.Calgary，Canada：[s.n.]，2014：1-4.

[12]王明新.數學物理方法[M].北京：清華大學出版社，2013：81-87.

[13]TAITELY，DUKLERAE.A model for predicting flow regime transition in horizontal and near horizontal gas-liquid flow[J].Aiche J.，1976，22（1）：47-55.

[14]XIAO J J，SHONHAM O，BRILL J P.A comprehensive mechanistic model for two-phase flow in pipelines[C]//SPE Annual Technical Conference and Exhibition.[S.l.]：Society of Petroleum Engineers，1990.

[15]HODNE K.Leak detection in two-phase oil and gas pipelines by parameter and state estimation[J].Institutt for Teknisk Kybernetikk，2008.

[16]DR.STUARTLSCOTT，DR.MARIAABARRUFET.Worldwide assessment of industry leak detection capabilities for single&multiphase pipelines（Project Report Prepared forthe Minerals Management Service Under the MMS/OTRC Cooperative Research Agreement）[R].35-01-99-CA-31003，2003.

Transient model and numerical calculation of gas-liquid two-phase flow pipeline leakage

CAIYongqiao1，LU Jin1，WANG Qing2，SUN Xiaoyang3，CAO Xuewen3
1.CNOOC Energy Development Equipment Technology Co.，Ltd.，Tianjin 300459，China
2.CNOOC Shandong ChemicalEngineering Co.，Ltd.，Jinan 250014，China
3.College of Pipeline and CivilEngineering，China University of Petroleum （Huadong），Qingdao 266580，China

There are many flow patterns in gas-liquid two-phase flow pipelines，and the relationship between flow parameters which would change once pipeline leakage happens is complicated.Analyzing the transient process of leakage is important to implement leakage detecting and locating of gas-liquid two-phase flow pipeline.A mathematical model of leakage system for gas-liquid pipeline is established and the leakage characteristics including pressure，liquid holdup，gas velocity and liquid velocity in stratified flow condition are analyzed.The control equations are solved by implicit difference method，and the leakage numerical solution of gas-liquid two-phase flow is calculated by C++programming.The solution shows that the pressure，liquid content rate in cross-section，velocities of gas and liquid at downstream of pipeline leakage point all drop as the leakage occurs.And the numerical results are in good agreement with the experimental data，proving that the established leakage modelhas a wellapplicability.

gas-liquid two-phase flow；stratified flow；leakage model；numericalcalculation；experimentalresearch

10.3969/j.issn.1001-2206.2017.06.006

蔡永橋（1983-），男，四川南充人，工程師，2007年畢業于西南石油大學過程裝備與控制工程專業，工程碩士，現主要從事管道智能檢測及管道完整性管理技術服務專業的研究工作。Email：caiyq3@cnooc.com.cn

2017-06-30