氣囊搬管法搬管過程的動力學分析

張大朋，白 勇，牛天鑫，朱克強

1.浙江大學建工學院，浙江杭州 310058

2.寧波大學海運學院，浙江寧波 315211

氣囊搬管法搬管過程的動力學分析

張大朋1，白 勇1，牛天鑫2，朱克強2

1.浙江大學建工學院，浙江杭州 310058

2.寧波大學海運學院，浙江寧波 315211

在海底管道鋪設、維修過程中，通常采用船舶搬管法對出現管道偏離原設計路由的情況進行糾偏，但困難大，風險高，為此提出了一種新的利用氣囊進行搬管的方法。結合某海域具體海況，運用OrcaFlex建立了氣囊搬管過程的動力學分析模型并進行計算。結果表明，氣囊安裝位置的管道彎矩、張力都會有一定驟變；離管道牽引端較近位置的管道張力比較大，管道中間位置張力變化不大，離管道固定端較近位置的管道張力比較小。0°波浪方向或180°海流方向管道的彎矩最大；最大彎矩位于沿管道長度方向300 m處；波浪和海流方向對管道最大彎矩的影響相比于氣囊安裝位置以及氣囊浮力的影響要小。

海底管道；氣囊搬管；動力學分析；OrcaFlex

海底管道是海洋油氣田開發的生命線。在海底管道鋪設和維修的施工過程中，有時會出現管道偏離原設計路由的情況，為了保證管道的后續安裝施工順利進行，需要把偏離的管道搬回原設計路由。目前常用的搬管方法是采用分布數個臨時固定式舷吊提升管道，然后通過船舶移動實現搬管[1-4]。搬管在海底管道安裝項目中，是施工難度較大和風險相對較高的作業，往往占用著大量的船舶資源，并且往往制約著整個項目工期和油田投產時間。特別是較大位移的搬管項目，傳統海上作業工作難度大、風險高、耗時長、不確定因素多。為了更好、更安全可靠地完成搬管作業，需要研究一種搬管的新方法。

本文主要參考某管道相關參數，提出了一種新的搬管方法，即利用氣囊搬管；并運用OrcaFlex建立了計算模型，得到初步方案；分析計算結果，分析時需要考慮施工作業載荷、環境載荷的影響，得到氣囊搬管方法可施行的海況。本研究工作對于具體工程實踐有一定的指導意義。

在本算例中管道總長為500 m，外徑為0.4 m，內徑為0.36 m，為控制管道的形態，不同位置的氣囊體積是不同的，氣囊提供的浮力為各個位置的氣囊體積與水的密度和重力加速度的乘積，在建模過程中，用Link單元將氣囊按照事先計算好的位置及坐標與管道相連接。

氣囊具體參數、布放位置及總體模型示意下文將作介紹。

1 理論模型

1.1 波浪流理論

目前JONSWAP譜已廣泛應用于實際工程中，本文采用JONSWAP譜作為波浪理論，其公式為[5]：

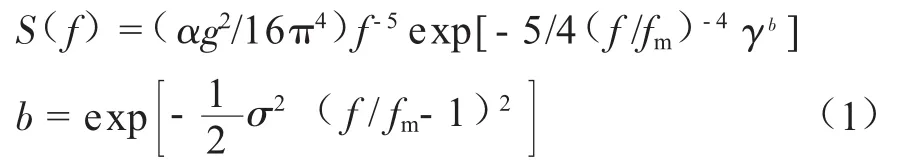
式中：S（f）為與頻率相關的譜函數，m2·s；α為Philips常數，無量綱，可由指定海況的有效波高Hs（m）和波浪平均周期TZ（s）計算；g為重力加速度，取9.8 m/s2；f為波浪頻率，Hz；fm為峰值頻率，Hz；γ為峰值增強因子，無量綱；σ為頻帶寬度標準差，m。

1.2 水動力理論

由于海底管道為細長構件，僅考慮波浪作用[2]，可采用修正后的Morison方程計算管道受到的波浪荷載[6]：

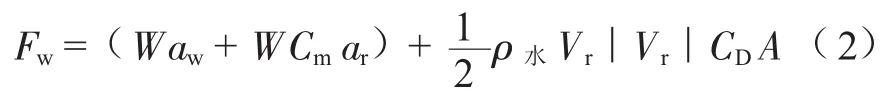
式中：Fw為波浪力，kN；W為排開水質量，t；aw為水相對海底加速度，m/s2；Cm為質量力系數，無量綱；ar為水相對物體加速度，m/s2；ρ水為海水密度，t/m3；CD為物體拖曳力系數，無量綱；Vr為水相對物體速度，m/s；A為拖曳面積，m2。

管道有效張力的表達式為[3]：

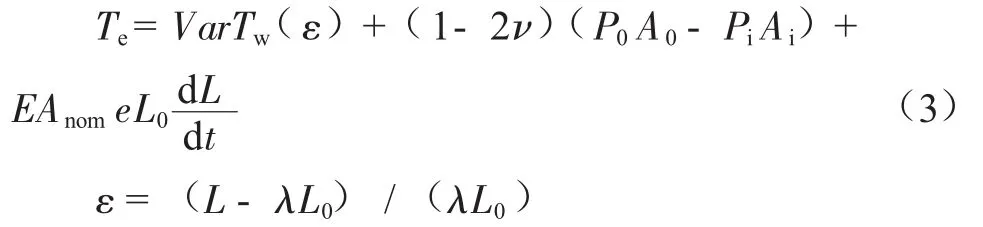
式中：Te為有效張力，kN；VarTw（ε）為關于應變ε的壁厚張力函數，kN；ν為泊松比，無量綱；P0、Pi分別為管道的內、外壓力，kN/m2；A0、Ai分別為管道內、外橫截面面積，m2；EAnom為標準軸向剛度，kN；e為管道的阻尼系數，m2/s；L0為管道未拉伸長度，m；L為管道單元初始長度，m；t為時間，s；dL/dt為長度增加速率，m/s；ε為總的平均軸向應變，無量綱；λ為膨脹系數，無量綱。

管道彎矩表達式為[7]：

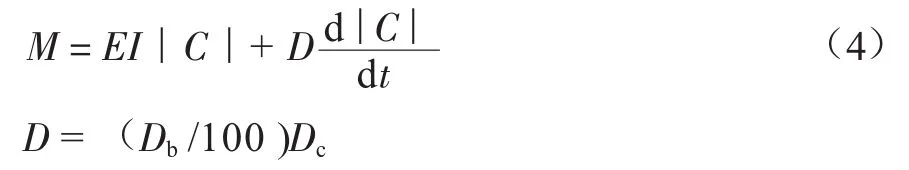
式中：M為管道彎矩，kN·m；EI為彎曲剛度，kN·m2；｜C｜為管道曲率，rad/m；d｜C｜/dt為曲率變化速率，rad/（m·s）；Db為彎曲阻尼，kN·m2；Dc為彎曲臨界阻尼值，kN·m2。

2 有限元模型

2.1 基本參數

管道基本參數和環境基本參數見表1和表2。最小屈服強度和極限抗拉強度均采用API 5L PSL2 X65 SMY規范值。

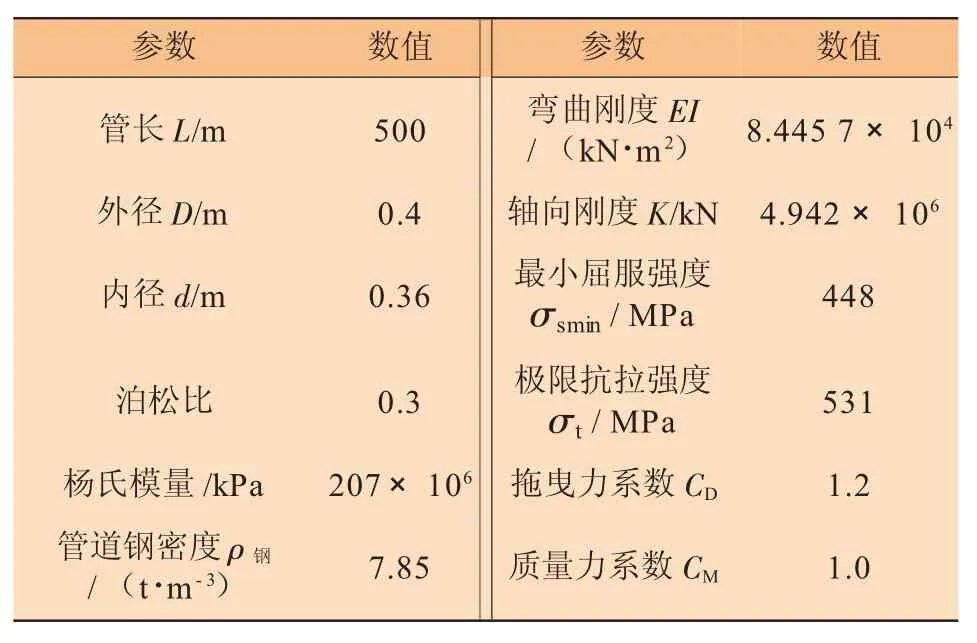
表1 管道基本參數

表2 環境基本參數

2.2 管道模型

本文基于凝集質量法對管道進行建模。OrcaFlex軟件是將管道看作為一系列連續Line單元，Line單元只具有質量，Line單元之間由無質量彈簧連接，通過Line單元和彈簧的應力-應變情況來反映管道的動態響應，如張力、彎矩等[8-11]。

2.3 氣囊模型

為了避免氣囊提升管道過程中，由于局部管道張力過大引起較大彎曲變形，從而產生過大應力導致管道斷裂，采用捆綁多個氣囊的方法來分擔管道張力，避免出現局部應力過大。3D Buoy單元有3個自由度，可以承受浮力、拖曳力、重力以及附加質量力等外部載荷的作用，模型采用11個3D Buoy單元模擬氣囊的作用。此外，設置3D Buoy的體積彈性模量為無限大，從而保證3D Buoy模擬的氣囊不發生變形。Winch單元為無質量的虛擬單元，3D Buoy可以通過Winch單元連接到管道的指定位置。3D Buoy單元模擬氣囊的相關數據見表3。

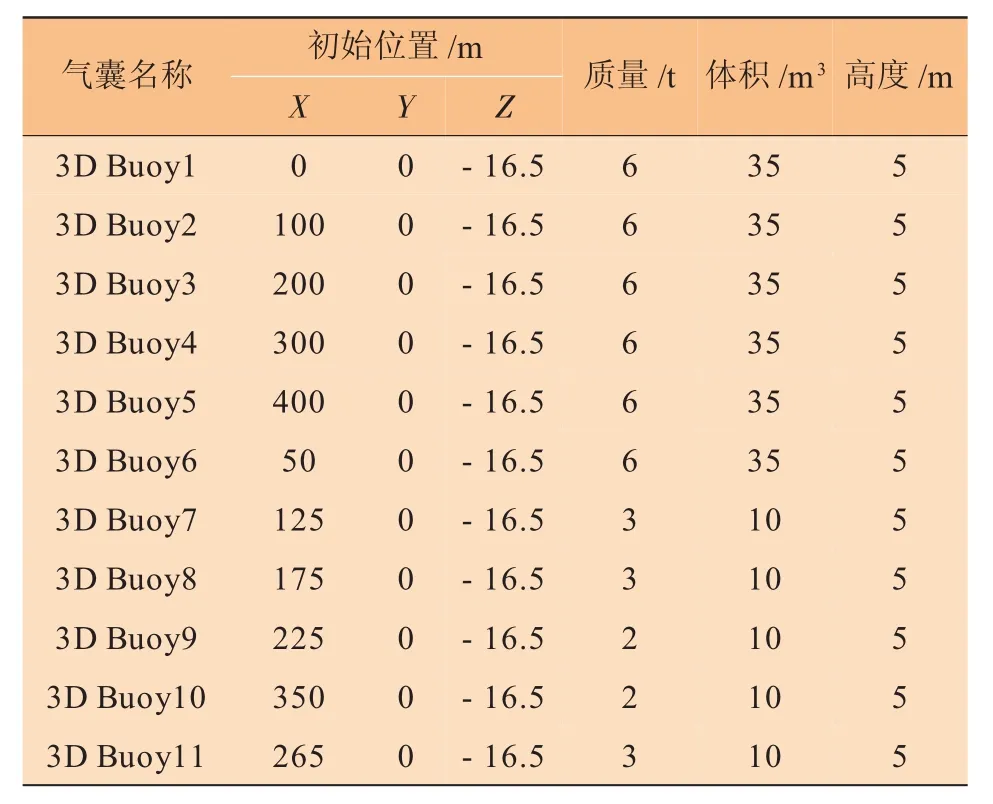
表3 3DBuoy單元模擬氣囊相關參數

2.4 模型建立

建立的模型是將管道從偏移路由移回到設計路由的過程，即將管道從A點移到C點，見圖1。管道End B固定，End A與錨鏈a端連接，目標位置C安裝絞盤，絞盤與錨鏈b端連接，氣囊將管道浮起后，絞盤回收，將管道拖到目標位置C。在OrcaFlex中建立的模型見圖2（為整體坐標系，與表3不同）。

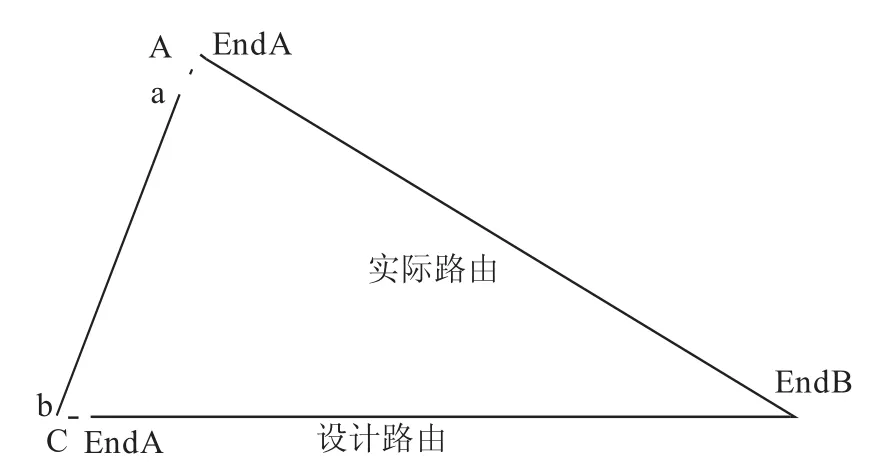
圖1 搬管路由

3 結果分析

為了說明波浪方向和海流方向對管道彎矩、張力的影響，分別建立管道在不同波浪方向、不同海流方向條件下的動態仿真模型，并進行分析。

圖2 模型示意

3.1 不同浪向管道彎矩、剪力結果分析

模型中的海流方向保持180°不變，波浪方向取0°～180°，每隔30°取一個浪向。

圖3為沿管道長度方向不同波浪方向下管道彎矩的曲線。圖3中出現峰值的位置為氣囊安裝位置，沿管道長度方向100、200、300、400 m位置的曲線比較尖，其他位置比較圓滑。產生的原因為氣囊安裝位置氣囊浮力對管道的影響占主導地位，波浪的影響相對較小。峰值較尖的位置即為氣囊浮力最大的位置。說明氣囊浮力對彎矩分布具有較大的影響。觀察圖3可知，氣囊安裝位置的彎矩會產生較大變化，搬管作業時應對此位置予以加強。

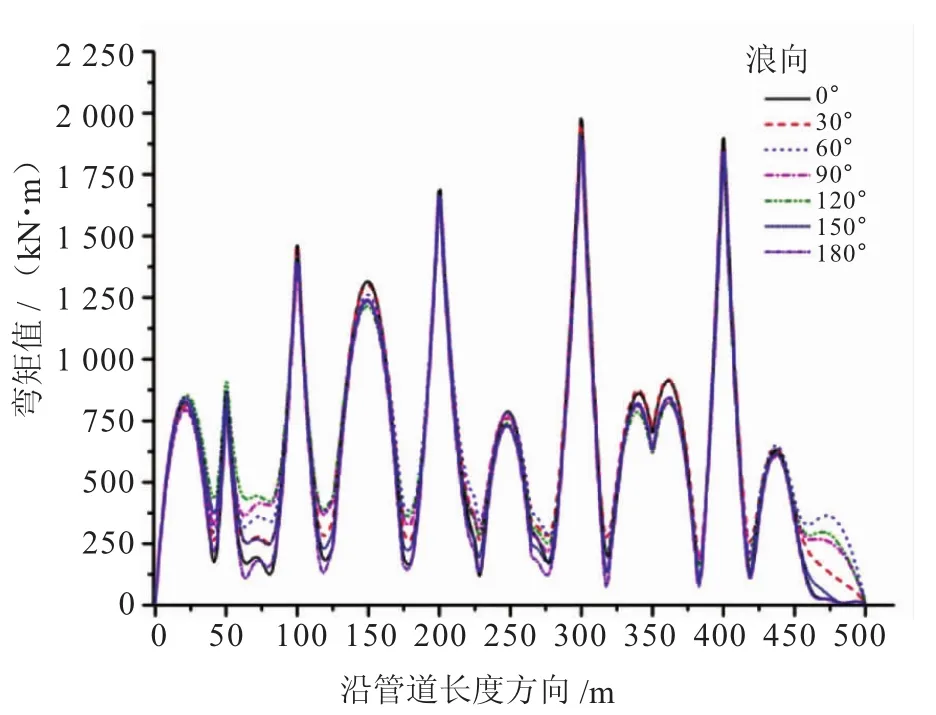
圖3 不同浪向下管道彎矩分布

圖4為沿管道長度方向管道最大張力和最大彎矩曲線分布。從圖4可以看出，張力值均為正值，說明管道處于拉伸狀態。管道的最大張力值，除了管道的首尾端，基本保持一個特定值（最大張力值約為46 875 kN），變化幅度并不是很大。進一步觀察圖4可知，管道長度在0～50 m位置之間時，最大張力逐漸降低，因為這段長度離牽引端較近，錨鏈對管道起主導作用，氣囊作用較小。End A與錨鏈連接，當絞盤回收錨鏈時，該位置瞬間產生拉力，因此該處張力最大。之后，錨鏈和絞盤對管道的影響逐漸減小，因此管道的最大張力也逐漸減小。管道長度位于50～400 m位置，由于錨鏈和絞盤對管道的影響很小，最大張力基本趨于平緩。管道長度位于400～500 m位置，由于End B固定，對管道起到束縛作用，離End B越遠，束縛作用越小，因此張力逐漸減小。觀察圖4可知，氣囊安裝位置的張力會產生驟變，且在大氣囊安裝位置的驟變比較顯著。

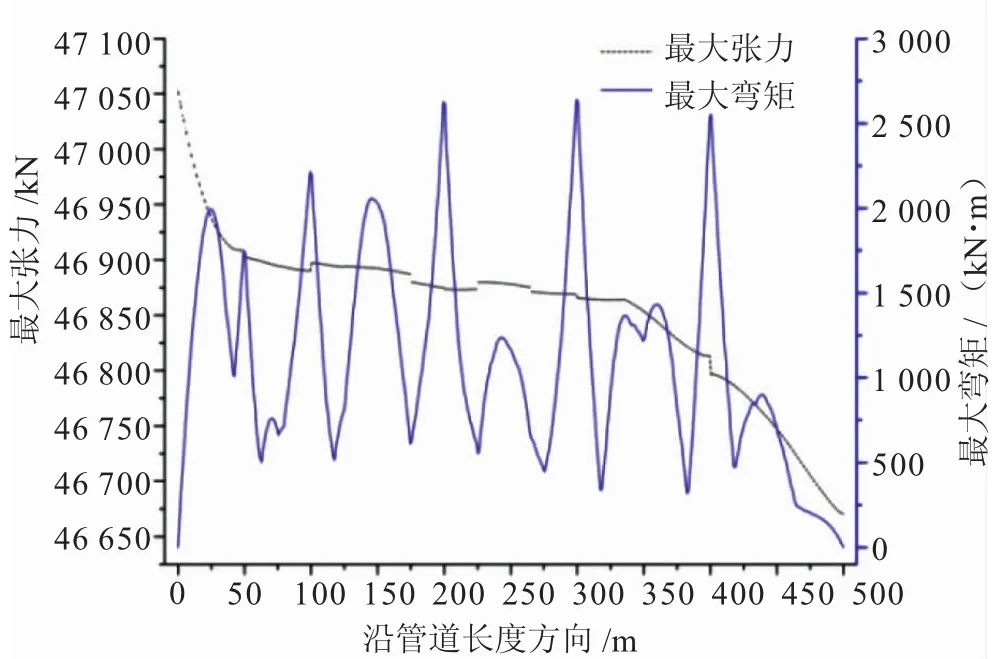
圖4 管道最大張力和最大彎矩曲線分布

最大張力取47 100 kN，計算可得最大抗拉強度為374.8 MPa，小于極限抗拉強度531 MPa，滿足管道強度要求。

由圖4可以看出，最大彎矩產生在沿管道長度方向300 m處。分析圖4可知，不同方向波浪作用下，當波浪方向為0°時，管道的彎矩最大，說明順浪對管道的彎矩影響較大，并且此時管道受到的內力、外力以及管道的變形都很大，因此應避免在此浪向下進行搬管作業。此外，對沿管道長度方向300 m處的管道應予以加強。

3.2 不同流向管道張力、彎矩結果分析

模型中的波浪方向保持180°不變，海流方向取0°～180°，每30°取一個流向。

圖5為不同海流方向下沿管道長度方向管道彎矩分布。圖6為沿管道長度方向管道最大彎矩和最大張力圖。圖5、6與圖3、4曲線趨勢分別基本相同，說明海流方向的變化對管道的影響相對較小，波浪方向的改變對管道牽拉過程中的影響占主導地位。

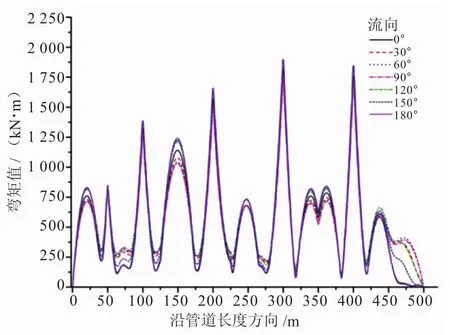
圖5 不同流向管道彎矩

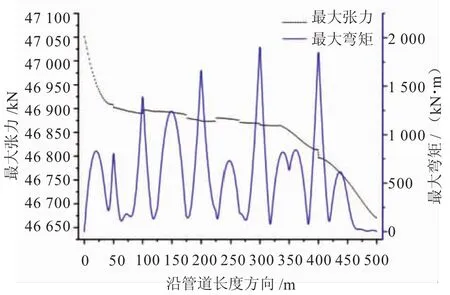
圖6 管道最大張力和最大彎矩

4 結論

（1）氣囊安裝位置的管道彎矩、張力都會有一定驟變，因此管道作業過程應予以特殊考慮，以便保證作業安全；離管道牽引端較近時管道的張力比較大，管道中間位置張力變化不大，離管道固定端較近時管道的張力比較小。

（2）波浪方向不同時，0°方向管道的彎矩最大；海流方向不同時，180°方向管道的彎矩最大；最大彎矩發生在沿管道長度方向300 m處，對此位置的管道，在進行設計以及作業時應著重考慮。

（3）波浪和海流方向對管道最大彎矩的影響相比于氣囊安裝位置以及氣囊浮力的影響要小。

[1]邊大勇，杜穎，劉建峰，等.海底埋設管線平管起吊運動分析[J].船舶工程，2015，37（12）：92-95.

[2]李盼，王曉飛，甘惠良，等.起管和搬管工藝的改進與應用[C]//第十五屆中國海洋（岸）工程學術討論會論文集（上）.北京：海洋出版社，2011：617-620.

[3]朱紹華.海底管道工程中立管的安裝方法[J].中國海上油氣，1999，11（3）：15-17.

[4]欒濤，潘東民，邊大勇，等.海底管道大位移平移設計及施工技術[J].中國造船，2015，56（2）：404-406.

[5]張大朋，朱克強，嚴心寬，等.不同浪向下船舶動力定位的動力學分析[J].水道港口，2015，36（4）：314-317.

[6]OrcaFLEX help file and user manual[M/OL].http://www.oricina.com.

[7]秦道武，朱克強，朱艷杰.基于凝集質量法的海洋纜索動態響應建模與仿真[J].港工技術，2014，51（3）：7-10.

[8]張大朋，朱克強，李園園，等.波流聯合作用下多分枝拖曳線列陣回轉過程的動力學分析[J].船舶工程，2015，37（11）：86-92.

[9]張大朋，朱克強，荊彪，等.文昌臍帶纜J型牽拉入位操作的水動力分析[J].船舶工程，2015，37（4）：92-97.

[10]張大朋，朱克強，李園園，等.不同Munk矩系數作用下海洋拖曳系統水動力響應分析[J].船舶工程，2016，38（4）：86-90.

[11]張大朋，朱克強.不同浪向下大型回轉式起重船回轉起吊作業過程的動力學分析[J].中國海洋大學學報（自然科學版），2017，47（5）：128-134.

Dynamic analysis of submarine pipeline moving with airbags

ZHANG Dapeng1，BAIYong1，NIU Tianxin2，ZHU Keqiang2
1.College of CivilEngineering and Architecture，Zhejiang University，Hangzhou 310058，China
2.Faculty of Maritime and Transportation，Ningbo University，Ningbo 315211，China

In submarine pipeline laying and maintenance，the method utilizing ships to move the pipeline deviating from its design route is often applied.But this method has big difficulty and risk.Combined with the specific sea conditions of a certain sea area，a new method of moving submarine pipeline with airbag is put forward and the dynamic analysis model is established by the nonlinear finite element software OrcaFlex.According to the calculation results，the bending moment and tension at the pipeline positions of installing airbags have rapid changes；the tension near the pipeline towing end is bigger，the tension at the pipeline middle position has less variation，the tension near the pipeline fixing eng is smaller.The pipeline maximum bending moment occurs along 0°or 180°wave direction and at the pipeline distance of 300 m.The influence of wave and current directions on pipeline maximum bending moment is less than the influence of airbag installation position and buoyancy.

submarine pipeline；pipeline moving with airbag；dynamic analysis；OrcaFlex

10.3969/j.issn.1001-2206.2017.06.003

長江學者和創新團隊發展計劃資助項目（IRT0734）；國家自然科學基金資助項目（11272160）。

張大朋（1987-），男，山東聊城人，助理研究員，2017年春季浙江大學建筑工程學院結構工程專業博士在讀，主要研究方向為船舶與海洋工程結構物動態響應。Email：1214265737@qq.com

2017-06-10