關于對p級數斂散性研究的注記

張國利， 杜智慧

(洛陽師范學院數學科學學院，河南洛陽 471934)

關于對p級數斂散性研究的注記

張國利， 杜智慧

(洛陽師范學院數學科學學院，河南洛陽 471934)

對于p級數收斂性，一般教材只給出了其隨參數p的收斂性和發散性.本文歸納總結了p級數中當參數p取1, 2, 3時的特殊情況下的研究歷史及一般情況下的推廣.

p級數；調和級數；巴塞爾問題；阿佩里常數；zeta函數

在p級數的教學過程中，很多教材都只給出了其斂散性的結論，對于各種情況下的斂散性研究過程卻沒有深入研究，本文嘗試對這個問題進行了一些探索.

我們把數項級數

(1)

稱為p級數，也稱超調和級數. 由積分判別法知， 當p>1時級數(1)收斂，p≤1時級數發散[1].

1 黎曼zeta函數

一般情況下，稱

(2)

為黎曼zeta函數，其中s為實部大于1的復數[2]. 由此可知某些情況下(1)是(2)的特例. zeta函數是數學中很重要的函數，它在解析數論中有著極其重要的地位， 尤其是與素數的分布有著密切的聯系，它在物理學、概率論和應用統計學中也有廣泛應用.當s取值負整數時，歐拉[3]首先證明了此時ζ(s)為有理數，并指出了它在模形式理論中的重要作用.

ζ(s)的一個積分表達式為

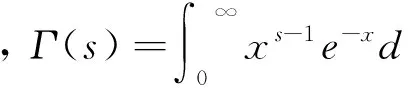
當s取正偶數2n時，ζ(2n)有一個簡潔的表達式，即

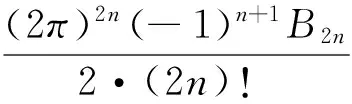
由上式，我們可以計算出ζ(2)、ζ(4)、ζ(6)、ζ(8)等數值，當s=-n,n為非負整數時，

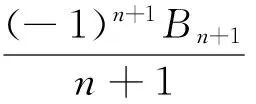
其中Bn為伯努利數，Bn用生成函數定義為

zeta函數與素數分布的密切關系體現在歐拉發現的恒等式中.

(3)

(3)式右端稱為歐拉乘積.由于s=1時，(3)式左端發散，由此可知素數有無窮多個.

1859年，黎曼證明了zeta函數滿足黎曼方……