不確定過程中增長性定理的一個證明
劉 樂, 賈耿華
(1.洛陽師范學院數學科學學院, 河南洛陽 471934; 2.洛陽理工學院數理部, 河南洛陽 471023 )
不確定過程中增長性定理的一個證明
劉 樂1, 賈耿華2
(1.洛陽師范學院數學科學學院, 河南洛陽 471934; 2.洛陽理工學院數理部, 河南洛陽 471023 )
不確定變量用來描述非確定性現象, 不確定過程就是一列隨時間或空間變化的不確定變量.本文對不確定過程的增長性態進行研究, 并給出相關證明.
不確定變量; 不確定過程; 增長性態
劉寶碇教授[1]于2007創立了不確定理論, 用以研究人類的主觀不確定性.作為處理主觀判斷或專家數據等不精確信息的新工具, 不確定性理論已引起了越來越多學者的關注, 已經成功應用于不確定規劃[2]、 不確定金融[3-4]、 不確定微分方程[3-4]等等領域中.
1 基本概念
定理1.1[1]令(Γ,L)是可測集, L是Γ的σ-代數, 稱Λ∈L為一個事件, 用M(Λ)來表示相信一個事件Λ會發生的信度. 如果M滿足以下幾條公理:
公理1.(正規性)M(Γ)=1;
公理2.(自對偶性)對任意事件Λ, 有
M(Λ)+M(Λc)=1;

定義1.1[1]不確定變量是從不確定空間(Γ, L, M)到實數集R的一個可測函數, 也就是說, 對任意R中的Borel集B, 集合{ξ∈B}={γ∈Γ|ξ(γ)∈B}是一個事件.
不確定積分是指不確定過程關于典范過程的積分.2009年, 劉寶碇教授[8]給出了一種重要的不確定過程典范過程的定義.
定義1.2[8]假設不確定過程Ct滿足如下三個條件:
(1)C0=0, 幾乎所有的軌道Lipschitz連續;
(2)Ct具有獨立穩態增量;



定理1.2[1](MarkovInequality)設ξ為一個不確定變量, 任給t>0和p>0, 我們有

2 不確定過程增長性定理

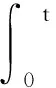
對于所有的t>0.

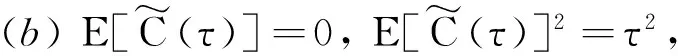




對所有的ε>0, 令
于是



又
等價于



(3)由(1),(2)即可推得
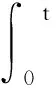
再由t(τ)的定義得


從而有




