圈圖在張量積下的獨(dú)立數(shù)

李晨瑩

(浙江師范大學(xué)數(shù)理與信息工程學(xué)院, 浙江金華 321004)

圈圖在張量積下的獨(dú)立數(shù)

李晨瑩

(浙江師范大學(xué)數(shù)理與信息工程學(xué)院, 浙江金華 321004)

圖G1，G2和G3的張量積(G1,G2,G3)定義為V(G1,G2,G3)=V(G1)×V(G2)×V(G3),[(u1,u2,u3),(v1,v2,v3)]∈E(G1,G2,G3)當(dāng)且僅當(dāng)|{i∶(ui,vi)∈Gi}|≥2.在本文中將證明， 當(dāng)G1,G2,G3均為圈圖時(shí)，等式α(G1,G2,G3)=max{α(G1)α(G2)|G3|,α(G1)α(G3)|G2|,α(G2)α(G3)|G1|}成立，并且還刻畫了其最大獨(dú)立集的結(jié)構(gòu).

EKR定理； 點(diǎn)傳遞； 本原性； 獨(dú)立數(shù)

1 引言及導(dǎo)語

令G和H兩個(gè)圖的直積圖G×H定義如下：

V(G×H)=V(G)×V(H),

[(u1,u2),(v1,v2]∈E(G×H)當(dāng)且僅當(dāng)(u1,v1)∈G且(u2,v2)∈H.

顯然，當(dāng)I是圖G(或H)的一個(gè)獨(dú)立集時(shí)，I×H(或G×I)是G×H的一個(gè)獨(dú)立集， 從而α(G×H)≥max{α(G)|H|,α(H)|G|}．Jha和KLav?ar[1]證明了這個(gè)不等式對某些非點(diǎn)傳遞圖等號是不成立的.1998年，Tardif[2]提出了等式

α(G×H)=max{α(G)|H|,α(H)|G|}

(1)

是否對所有的點(diǎn)傳遞圖G和H都成立的公開問題.如果G×H中的一個(gè)獨(dú)立集S能寫成A×B的形式，我們稱S是規(guī)則的.如果G×H中的每一個(gè)極大獨(dú)立集都是規(guī)則的，那么我們稱G×H是MIS-正規(guī)的.1996年， Frankl[3]證明了等式(1)對Kneser圖是成立的.

定理1[3]設(shè)n1,n2,…,nk和r1,r2…rk是正整數(shù)，2ri≤ni,1≤i≤k.那么

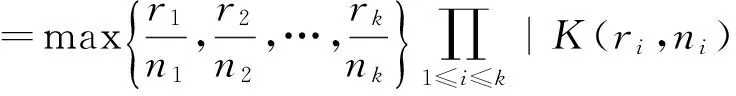
在圖論中，圈圖Kn:r(2r≤n)的頂點(diǎn)集是[n]，頂點(diǎn)i和j之間無邊相連當(dāng)且僅當(dāng)|i-j|≤r或 |n-i+j|≤r.顯然圖α(Kn:r)=r. 2006年，Valencia-Pabon and Vera[5]得到了圈圖直積的獨(dú)立數(shù).

2002年，B.Larose和C.Tardif[4]分別確定了Kneser圖、圈圖做任意次直積后的獨(dú)立集結(jié)構(gòu).

定理2[4](1)Kk(r,n) (2r

定理3[5]設(shè)n1,n2,…,nk和r1,r2…rk是正整數(shù)，2ri≤ni,1≤i≤k.那么

2007年，Ku和Wong[6]研究了對稱群的獨(dú)立數(shù)和MIS-正規(guī)性質(zhì).

定理4[6]設(shè)n1,n2,…,nk是正整數(shù)，那么

并且直積Sn1×Sn2×…×Snk是MIS-正規(guī)的，除非存在i，j和l使得下面三種情況之一成立：

(1)ni=nj=nl=2;

(2)ni=nj=3;

(3)ni=2且nj=3.

Albertson and Collins[7]在1985年提出了非同態(tài)引理，它對確定點(diǎn)傳遞圖的獨(dú)立集的上界是十分有效的.

引理1[7]設(shè)G和H是兩個(gè)圖，如果G是點(diǎn)傳遞的并且存在一個(gè)同態(tài)映射φ:H→G，那么

在引理1中，取H為G一個(gè)誘導(dǎo)子圖，φ是從H到G的嵌入映射，我們會(huì)得到如下引理.

由引理2可以得到以下命……