滾動時域狀態估計中極小化問題的求解

胡 磊，伊國興，南 熠

(哈爾濱工業大學航天學院，黑龍江 哈爾濱 150001)

滾動時域狀態估計中極小化問題的求解

胡 磊，伊國興，南 熠

(哈爾濱工業大學航天學院，黑龍江 哈爾濱 150001)

滾動時域狀態估計(MHSE)方法的基本思想是：將控制系統的狀態估計問題轉化為有限時域內的優化問題，通過獲得的優化解對系統狀態進行估計。針對帶約束的線性離散系統的狀態估計問題，介紹了MHSE方法的研究及應用現狀。基于懲罰函數法建立懲罰因子，將約束條件融合到適應度函數中，通過粒子群優化(PSO) 算法求解MHSE方法中的極小化問題。基于Matlab編程，實現了二階仿真算例。仿真結果表明，PSO算法能夠有效地求解MHSE方法中的極小化問題，使得2種狀態的估計值和真實值之間的均方差分別為0.075 0、 0.204 1。PSO算法能夠有效地求解二階仿真算例，以獲取滾動時域估計方法中極小化問題的最優解，為基于MHSE方法進行狀態估計的研究與應用提供了參考。下一步的研究方向是提高估計精度，以及復雜約束條件下高階系統的極小化問題的求解。

狀態估計； 適應度函數； 滾動窗口； 約束； 極小化； 粒子群優化算法； 懲罰函數

0 引言

許多控制系統往往需要通過狀態反饋對系統進行優化，以達到性能指標要求。然而，并非所有的系統狀態變量均易于直接檢測，有些狀態變量甚至根本無法檢測[1]。此外，在實際系統中，外部干擾往往存在約束，例如干擾具有下界或者在某個范圍內波動。為了優化上述類型的控制系統，研究帶約束的系統狀態估計是十分有意義的。

滾動時域狀態估計(moving horizon state estimation，MHSE)方法自提出以來，受到了工程界眾多學者的關注。MHSE方法對于工業過程的參數估計和狀態估計問題，具有良好的效果[2]。該方法將估計問題轉化為優化問題，同時又能包含系統的約束條件，利用在線滾動優化原理進行狀態估計[3]。文獻[4]將MHSE方法應用于具有不確定性的冰山漂移預測。文獻[5]將MHSE方法應用于帶有未知輸入的線性離散系統的狀態估計。文獻[6]將MHSE方法應用于具有參數不確定系統的狀態估計。但以上文獻都未具體指出MHSE方法中極小化問題的求解方法。因此，研究其求解方法是十分有意義的。針對上述問題，建立懲罰因子，對具有上下界的狀態約束進行處理；采用粒子群優化(particle swarm optimization,PSO)算法對MHSE方法中的極小化問題進行求解，得出系統的初始狀態和擾動，實現了對系統狀態變量的估計。

1 滾動時域狀態估計方法

MHSE方法基于測量輸出來估計系統狀態。考慮如式(1)所示的線性離散系統。系統滿足條件xk∈X、uk∈U、ωk∈W、vk∈V，域W、X、V、U為凸集。

(1)

式中：xk∈Rn為系統狀態；uk∈Rg為系統輸入；yk∈Rp為測量輸出；ωk∈Rm為外部干擾；vk∈Rp為測量噪聲。

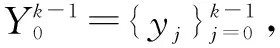
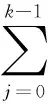
(2)

式中：j為粒子數。

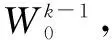
全信息MHSE方法將線性離散系統(1)的狀態估計問題描述為如下所示的數學規劃問題1。

問題1[6]：

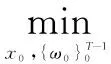
(3)

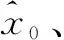
式(3)滿足時域約束條件和動力學方程，分別為：

式中：D為單個粒子的維數。

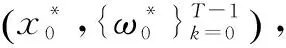
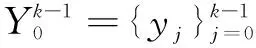
近似MHSE方法將線性離散系統(1)的狀態估計問題描述為如下所示的數學規劃問題2。

問題2[6]：

(4)

式(4)滿足時域約束條件和動力學方程，分別為：

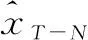
Πk+1=BQB′+A(Πk-ΠkC′(R+CΠkC′)-1CΠk)A′

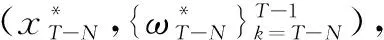
2 粒子群優化算法

PSO算法的基本思想是：基于迭代所積累的自身經驗以及全局經驗，更新粒子的速度和位置，將當代粒子代入適應度函數中求值，并與歷史最佳適應度函數值相比較，選取滿足目標問題且使之最優的解。PSO算法易于實現、參數較少，能有效解決復雜優化任務[7-9]。因此，針對外部擾動有下界的線性離散系統，在基于MHSE方法實現其狀態估計時，選擇PSO算法對MHSE方法中的極小化問題進行求解，以期獲得包含初始狀態和干擾的最優解，進而實現系統的狀態估計。

粒子的速度和位置更新公式如下：

式中：t為迭代次數；粒子數j=1,2，…，n，n為整個種群的大小；α1和α2為(0,1)中隨機抽取的均勻隨機數；η為慣性權重；μ1和μ2為加速度權重系數；Xj=[xj,1,xj,2,…,xj,D]為第j個粒子的位置；vj=[vj,1，vj,2,…,vj,D]為第j個粒子的速度；Sj=[sj,1，sj,2,…,sj,D]為第j個粒子的歷史最佳位置。

第(t+1)次迭代時，粒子的歷史最佳位置的計算公式如下：

式中：f(·)為適應度函數。

第(t+1)次迭代時，粒子群體歷史最佳位置的計算公式如下：

式中：S0=[s0,1,s0,2,…，s0,D]為群體的歷史最佳位置。

3 模型建立

針對式(1)所示的線性離散系統，假設輸入u(k)=0，測量輸出集合為Y=[y0，y1，…，yT-1]T，分別考慮外部干擾沒有約束條件以及外部干擾在某個給定范圍內波動這一約束條件，建立了無約束條件模型和有約束條件模型。

3.1 無約束條件模型

當T≤N時，定義X=[x0,ω0,ω1,…,ωT-1]T，由式(4)定義如下適應度函數。

推導得：

(5)

當T>N時，定義X=[xT-N，ωT-N，ωT-N+1，…,ωT-1]T，由式(4)定義如下適應度函數。

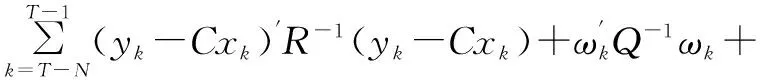
推導得：

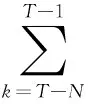
(6)

3.2 有約束條件模型

約束優化問題是科學研究和工程應用中普遍存在的一類優化問題[10]。通常，處理約束優化問題的方法主要有修理法、丟棄法和懲罰函數法等。懲罰函數法將約束優化問題中的違反約束項乘以懲罰項并加到目標函數中，從而構造出帶參數的增廣目標函數[11]。針對約束條件ωk≥0，懲罰函數法能夠更好地處理約束條件，求取優化目標解。

因此，本文選取懲罰函數法對約束進行處理。具體過程是：建立懲罰因子δ，將約束優化問題中的約束條件ωk≥0融合到適應度函數中，進而用粒子群優化方法來求解。構造如下懲罰函數和目標函數。

(7)

F(X,δ)=f(X)+δ×P(X)

(8)

式中：δ為懲罰因子，取正數，大小視實際仿真情況而定；f(X)來自式(5)、式(6)。

以F(X,δ)作為新的適應度函數：當X是目標解時，P(X)=0，F(X,δ)=f(X)；當X不是目標解時，P(X)>0，δP(X)>0，F(X,δ)>f(X)，使得X代入目標函數所得的解不是最小值，需要進一步迭代尋優。

4 估計系統仿真試驗

作為驗證PSO算法能夠求解極小化約束問題的仿真示例，考慮約束條件為ω(k)≥0、輸入u(k)=0的線性離散系統為[6]：

(9)

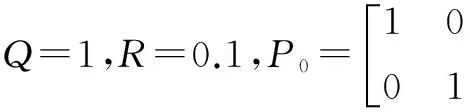
圖1 仿真結果(無約束,N=1)

取滾動時域窗口長度N=1，對有約束條件下線性離散系統(9)的狀態x1和x2進行仿真，結果如圖2所示。圖2中，估計值和真實值之間的均方差為σ1=0.091 4、σ2=0.317 4。

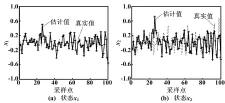
圖2 仿真結果(有約束,N=1)

取滾動時域窗口長度N=4，對有約束條件下線性離散系統(9)的狀態x1和x2進行仿真，結果如圖3所示。圖3中，估計值和真實值之間的均方差為σ1=0.075 0、σ2=0.204 1。

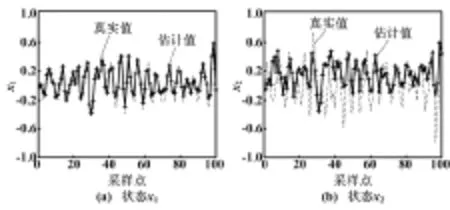
圖3 仿真結果(有約束,N=4)

從圖1～圖3及其對應的σi值可以看出，針對二階線性離散系統(9)，可基于PSO 算法求解MHSE方法中的極小化問題，得出系統的初始狀態和干擾，進而求出當前時刻的狀態估計。

5 結束語

針對線性離散系統狀態估計問題，深入分析了滾動時域估計方法，通過嚴格的數學推導，得到了適應度函數表達式，并研究了無約束條件的線性離散系統。采用PSO優化算法對適應度函數進行尋優，并研究了有約束條件的線性離散系統。采用懲罰函數法來處理該約束條件，將約束條件融合到增廣目標函數中，生成新的適應度函數，并采用PSO優化算法求解。基于Matlab編程,實現了對1個二階實例的仿真驗證。仿真結果表明，PSO算法能夠對MHSE方法中的極小化問題進行求解，PSO算法結合懲罰函數法能夠對有下界的外部干擾進行處理。

盡管PSO算法實現了對MHSE方法中極小化問題的求解，但是對于如何提高估計精度，以及對復雜約束條件下高階系統的極小化問題的求解，仍需要進一步探討和研究。

[1] 王紅,吳險峰,張友.離散時間模糊控制系統的新型狀態觀測器設計[J].數學的實踐與認識,2015,45(16):152-158.

[2] ZAVALA V M,BIEGLER L T.Optimization-based strategies for the operation of low-density polyethylene tubular reactors:moving horizon estimation[J].Computers & Chemical Engineering,2009:33(1):379-390.

[3] ANGELO A,MAURO G.Moving-horizon estimation for discrete-time linear and nonlinear systems using the gradient and Newton methods[C]//Conference on Decision and Control(CDC).Las Vegas:IEEE,2016:2906-2911.

[4] LEIFERIK A,FRANCESCO S,LARS I.The moving horizon estimator used in iceberg drift estimation and forecast[C]//European Control Conference(ECC).Denmark:IEEE,2016:1271-1277.

[5] BOULKROUNE B,DAROUACH D,ZASADZINSK M.Moving horizon estimation for discrete time linear systems with unknown inputs[C]//Proceedings of the European Control Conference 2007.Greece:IEEE,2007:2875-2878.

[6] 趙海燕.時域約束系統的滾動時域狀態估計方法研究[D].長春:吉林大學,2007:14-21.

[7] 王東,風孟麗,趙文杰.基于自適應搜索中心的骨干粒子群算法[J].計算機學報,2016,39(12):2652-2667.

[8] 鄧麗,蔣婧,費敏銳.基于免疫粒子群算法的PID參數整定與自適應[J].自動化儀表,2013,34(2):65-67.

[9] 楊琳,孔峰.嵌入粒子群優化算法的混合人工蜂群算法[J].自動化儀表,2013,34(1):50-53.

[10]劉云連,伍鐵斌,王俊年,等.改進罰函數法與蝙蝠算法在約束優化中的應用[J].計算機工程與應用,2015,9(9):62-67.

[11]蔡海鸞.懲罰函數法在約束最優化問題中的研究與應用[D].上海:華東師范大學,2015:5-6.

SolutionoftheMinimizationinMovingHorizonStateEstimation

HU Lei,YI Guoxing,NAN Yi

(School of Astronautics,Harbin Institute of Technology,Harbin 150001，China)

The basic idea of moving horizon state estimation(MHSE) method is to convert the state estimation of the control system into the optimization in the finite time domain,and obtain the optimal solution to implement estimation of system state.In order to solve the state estimation of linear discrete systems with constraints,the research and current status of application of MHSE method are presented.The penalty factor is established based on the penalty function method,the constraint condition is integrated into the fitness function,and the minimization in the MHSE method is solved by the particle swarm optimization(PSO) algorithm.On the basis of Matlab programming,the second order simulation case is realized. The simulation results show that the PSO algorithm can effectively solve the minimization in the MHSE method,so that the mean square error between the estimated value and the true value of the state andis 0.075 0 and 0.204 1.The PSO algorithm can effectively solve the second-order simulation case,to obtain the optimal solution of the minimization in the moving horizon state estimation method,which provides reference for the research and application of state estimation based on MHSE method.The next step is to improve the estimation accuracy and solve the minimization of the high order system with complex constraints.

State estimation; Fitness function; Moving window; Constraint; Minimization; PSO algorithm; Penalty function

修改稿收到日期:2017-07-26

胡磊(1993—)，男，在讀碩士研究生，主要從事智能算法的研究，E-mail：maple_hsjz@163.com；伊國興(通信作者)，男，博士，教授，主要從事先進導航與無人機智能控制等方向的研究,E-mail：ygx@hit.edu.cn

TH-3；TP13

A

10.16086/j.cnki.issn1000-0380.201712011