任意正多邊形小孔夫瑯禾費衍射成像探討
宋易知
(北京師范大學 物理學系,北京 100875)
任意正多邊形小孔夫瑯禾費衍射成像探討
宋易知
(北京師范大學 物理學系,北京 100875)
對夫瑯禾費衍射積分進行了理論推導,基于夫瑯禾費衍射積分公式的一般形式,推導出了一種對任意正多邊形小孔夫瑯禾費衍射情況的計算方法,并利用Matlab軟件進行計算機模擬,做出了只用1個函數文件即可計算出所有可能的多邊形小孔夫瑯禾費衍射成像的嘗試.
正多邊形小孔;夫瑯禾費衍射;Matlab
1 理論基礎
光的衍射現象能體現光的波動性,即光在直線傳播中遇到圓孔、小球、直邊等障礙物時,不被擋住反而繞到其后面傳播,進入光強本應為零的暗區[1-2]. 惠更斯-菲涅耳原理以波動理論解釋光如何傳播,指出波陣面上每一點均為次波源,這些次波的包絡面即為新波面.
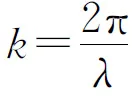
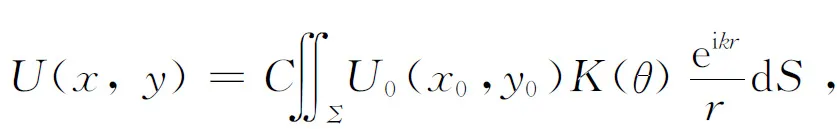
(1)
其中C為比例系數,K(θ)為傾斜因子[當θ增大時,K(θ)緩慢減小],Σ為平面波的1個波面[3].
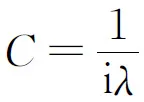

(2)

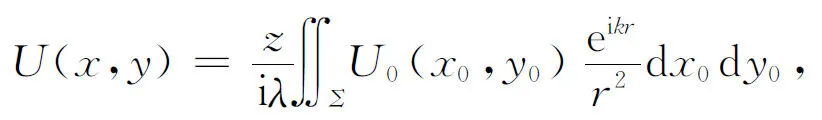
(3)
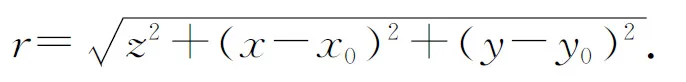
在通常的光學處理系統中,z應遠遠大于衍射小孔和觀察區域的最大線度,且從P到Q點的距離應遠遠大于光的波長,即r?λ,相當于用平面波的振幅替代球面波前在觀察平面上產生的復振幅[3]. 易推知θ應為小量,則有
K(θ)=cosθ≈1 .
(4)
雖然(3)式分母中的r可以直接用z代替,但不能忽略的是,當λ很小時,k值很大,指數中的r的微小誤差可能引入遠大于2π的相位變化,使之不可以直接用z代替. 對其做二項式展開[4]
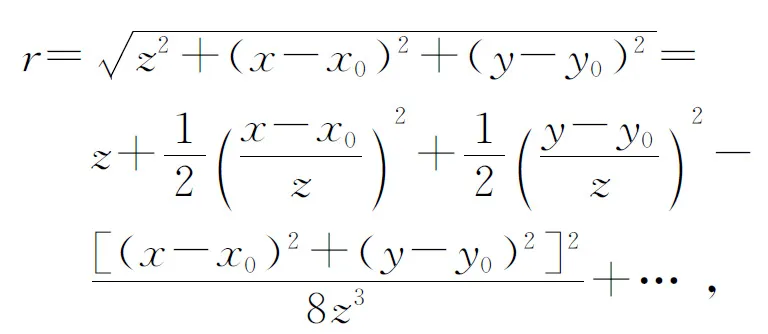
(5)
保留展開式的前兩項,有
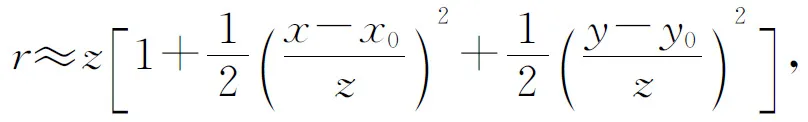
(6)
于是得到了菲涅耳衍射積分
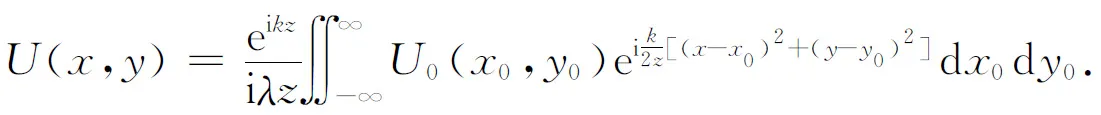
(7)
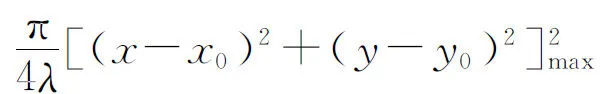
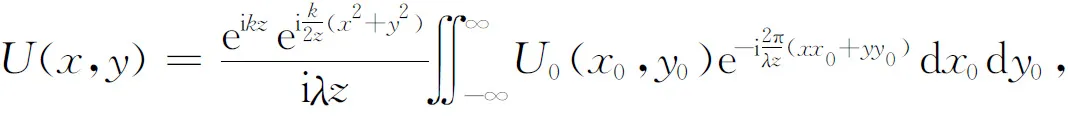
(8)
即在夫瑯禾費衍射區內觀察平面上的夫瑯禾費衍射積分公式的一般形式.
2 計算原理
2.1 計算思路
如圖1所示,由于正多邊形的中心對稱性,對于正L邊形的小孔,只需要計算出1個小三角形的衍射場分布,將其進行L-1次坐標旋轉變換,隨后將其全部相加,就能獲得任意正多邊形小孔的夫瑯禾費衍射成像. 此前的衍射成像模擬程序都局限在某個特定形狀小孔上,而在這種思路的指導下, 本文做出了只用1個函數文件計算出所有可能的多邊形小孔夫瑯禾費衍射成像的嘗試.

圖1 正多邊形由多個小三角形組成
2.2 等腰三角形孔的夫瑯禾費衍射
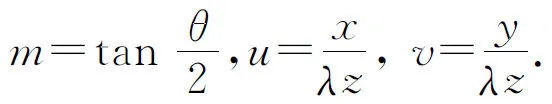
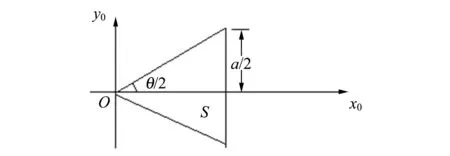
圖2 等腰三角形孔
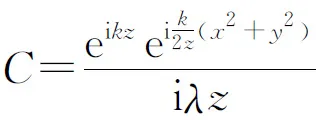
(9)
2.3 正多邊形孔的夫瑯禾費衍射
如果衍射屏為邊長為a的正n邊形孔(如圖3),則以其幾何中心為原點,建立坐標系. 由于S=S1+S2+…+Sn,這樣夫瑯禾費衍射積分就可以分別在這n個三角形區域進行,由于這n個三角形是全等的,其積分結果應當對稱. 可從S1的衍射結果式(9)出發,依次繞z軸旋轉θ角,即對式(9)依次作下列坐標變換:

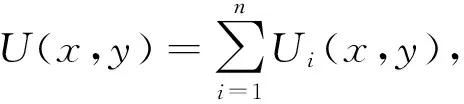
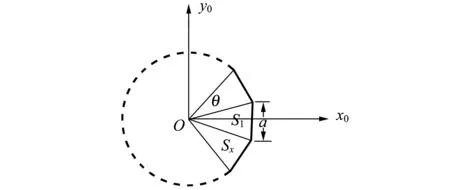
圖3 正n邊形孔
由此,得到了正多邊形小孔的夫瑯禾費衍射的計算方法. 原則上存在任意多邊形孔的夫瑯禾費衍射公式,但是將每個都計算出來極其繁瑣且不具操作性. 因此,不妨考慮用計算機程序模擬的方法解決這個問題.
3 Matlab模擬
3.1 程序
根據以上計算分析編寫夫朗禾費任意多邊形小孔衍射仿真函數文件(運行環境:Matlab R2014b)[6]:
function dbx(L) %L是邊數
the=pi*(L-2)/L; %多邊形的外角
m=tan((pi-the)/2); %等腰小三角形頂角的1/2
a=3e-5;
lamda=500e-9; %光的波長
z=6; %衍射屏到觀察屏的距離
k=2*pi/lamda;
h=a/(2*m*lamda*z);
x=-1∶0.005∶1;
y=-1∶0.005∶1;
for i=1∶1∶401
for j=1∶1∶401
for n=1∶L
C=a*exp((-1)^(1/2)*k*z)*exp((-1)^(1/2)*k*((x(i))^2+(y(j))^2)/2/z)/(4*pi*m*y(j));
alpha=h*(x(i)+m*y(j));
beta=h*(x(i)-m*y(j));
E1(n,i,j)=C*(exp(-(-1)^(1/2)*pi*alpha)*sin(alpha)/alpha-exp(-(-1)^(1/2)*pi*beta)*sin(beta)/beta);%單個小三角形的衍射場
u(i)=x(i); %x和y分別轉過一角度
x(i)=x(i)*cos(the)+y(j)*sin(the);
y(j)=-u(i)*sin(the)+y(j)*cos(the);
end
E(i,j)=sum(E1(∶,i,j)); %L個小三角形相加
I(i,j)=abs(E(i,j))^2; %求光強
end
end
m=max(I(∶));n=min(I(∶));I0=(I-n)/(m-n);
figure(1)
imshow(I0) %畫圖
figure(2)
mesh(I)
3.2 運行結果
3.2.1 正三角形小孔
在指令窗口輸入“〉〉dbx(3)”得到圖像如圖4所示.
3.2.2 正四邊形小孔
在指令窗口輸入“〉〉dbx(4)”,得到圖像如圖5所示.

(a)
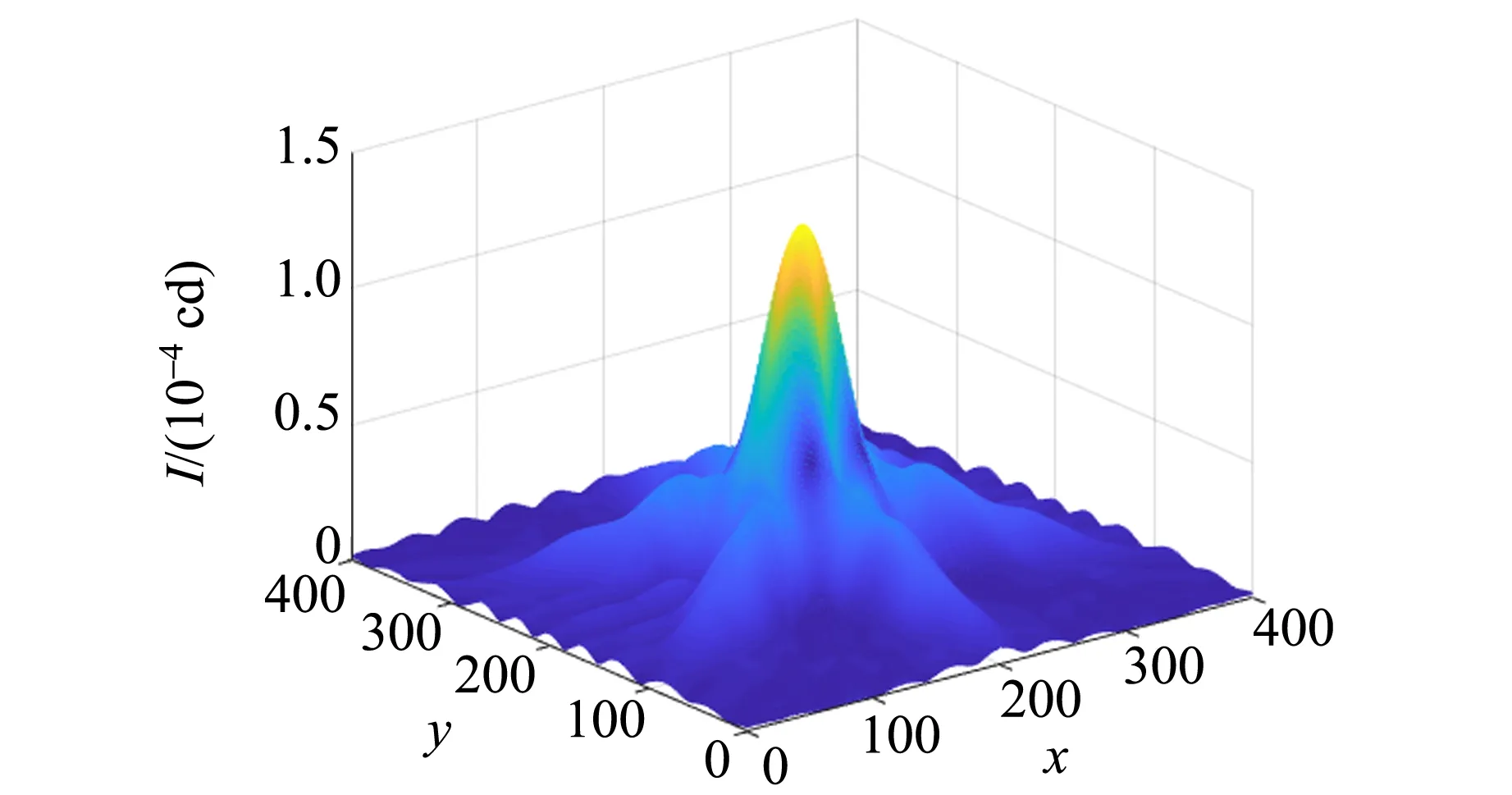
(b)圖4 正三角形小孔衍射圖樣

(a)
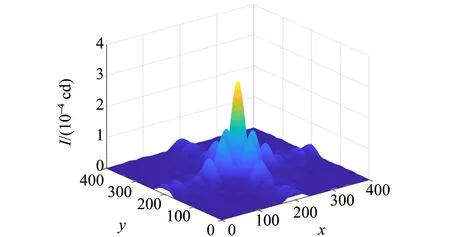
(b)圖5 正四邊形小孔衍射圖樣
3.2.3 正五邊形小孔
在指令窗口輸入“〉〉dbx(5)”,得到圖像如圖6所示.
3.2.4 正六邊形小孔
在指令窗口輸入“〉〉dbx(6)”,得到圖像如圖7所示.

(a)
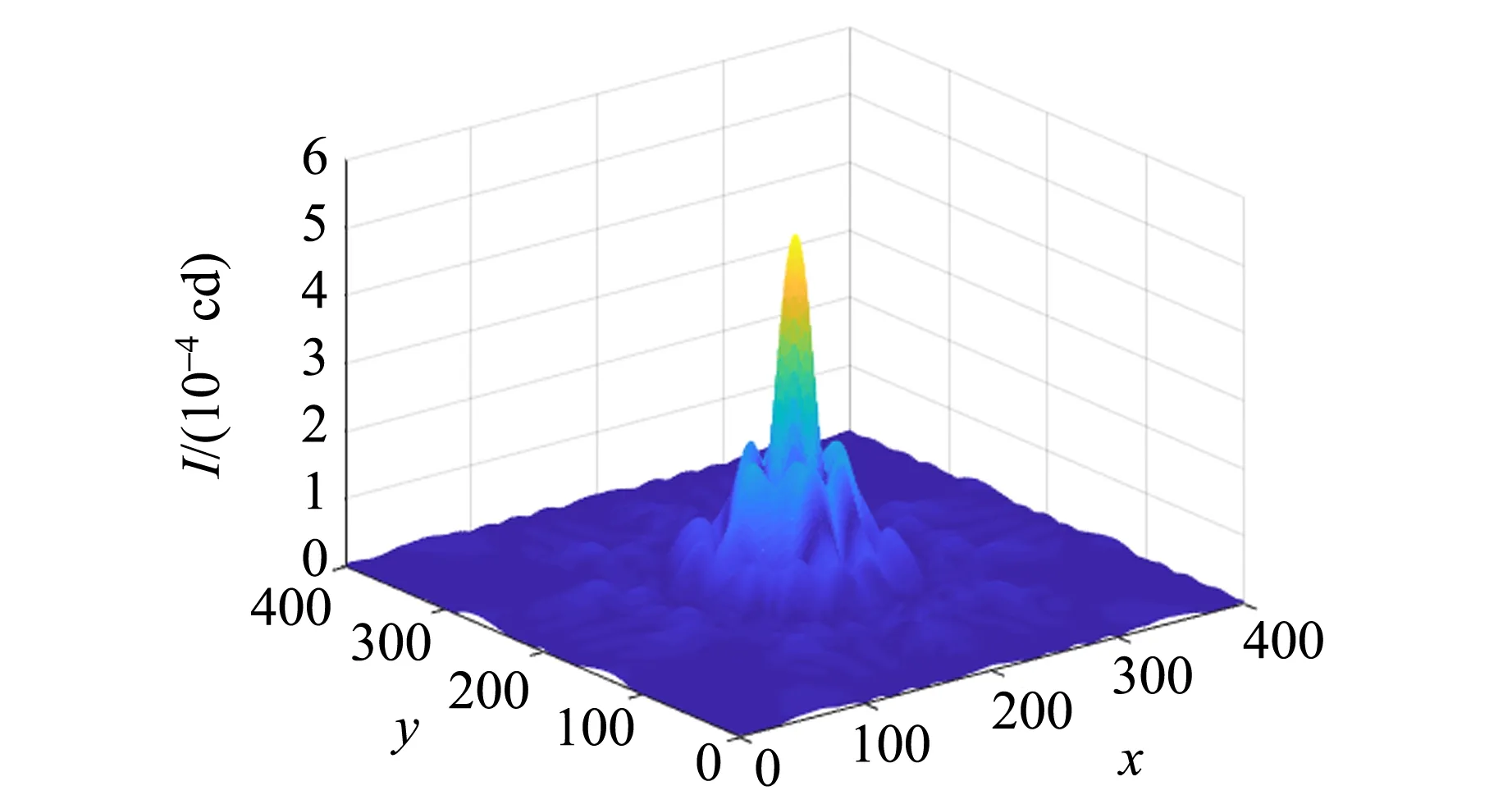
(b)圖6 正五邊形小孔衍射圖樣

(a)
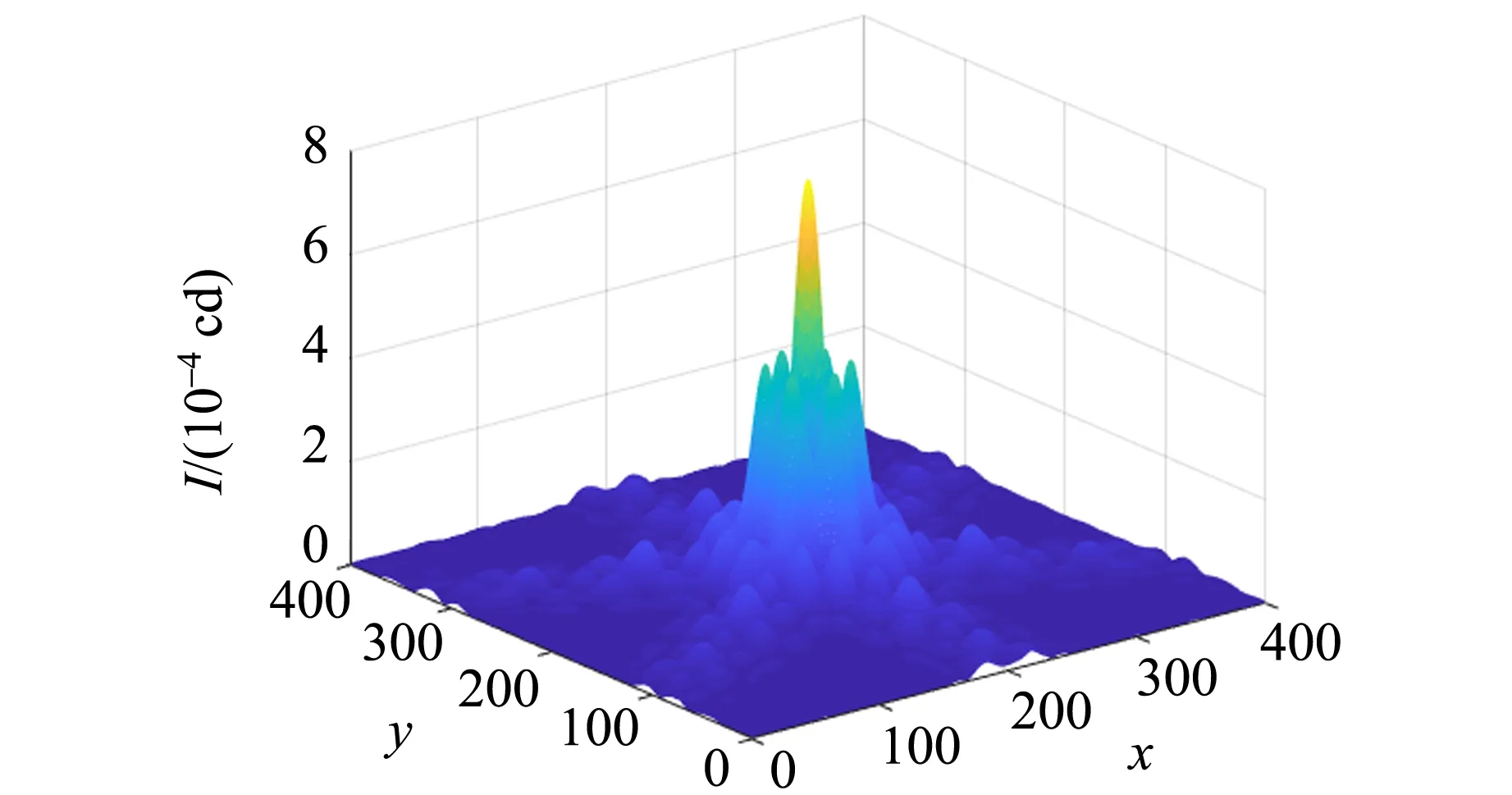
(b)圖7 正六邊形小孔衍射圖樣
4 結束語
在當今社會,計算機技術迅猛發展并日臻完善,基于Matlab 的計算機模擬技術對物理研究的幫助日趨顯著. 由計算機模擬結果可見,衍射圖樣為旋轉對稱圖形,且在正多邊形各邊的垂直方向上光強較強;邊數越多,光強較強的區域越密集. 不難推斷,當n→∞時,光強分布為圓形亮斑外套著明暗相間的圓環,即圓孔的夫瑯禾費衍射圖樣. 可以看到,計算機模擬的正五邊形的衍射圖樣由于排布十分密集,已經接近圓孔的夫瑯禾費衍射圖樣.
致謝:衷心感謝計算物理老師彭芳麟教授的教導!
[1] 姚啟鈞. 光學教程[M]. 5版. 北京:高等教育出版社,2014.
[2] 加塔克.光學[M]. 梁銓廷,胡宏章,譯. 北京:機械工業出版社,1984:74-85.
[3] 厲江帆,姜宗福,黃春佳,等. 夫瑯禾費衍射公式的一般形式[J]. 大學物理,2003,22(11):9-14.
[4] 于愛軍. 光的多邊形衍射的計算機模擬[D]. 大連:大連理工大學,2007.
[5] Joseph W G. Introduction to Fourier optics [M]. 北京:電子工業出版社,2006:59-67.
[6] 彭芳麟. 計算物理基礎[M]. 5版. 北京:高等教育出版社,2010.
DiscussionontheFraunhoferdiffractionimagingofarbitraryregularpolygonhole
SONG Yi-zhi
(Department of Physics, Beijing Normal University, Beijing 100875, China)
Based on the general form of Fraunhofer diffraction integral, the calculative method to analyze arbitrary regular polygon Fraunhofer diffraction was put forward. Using the Matlab software, computer simulation was carried out, attempting to get all possible Fraunhofer diffraction imaging of the regular polygon hole with just one function file.
regular polygon hole; Fraunhofer diffraction; Matlab
O436.1
A
1005-4642(2017)11-0048-04

2017-06-05;修改日期2017-07-07
宋易知(1998-),女,四川樂山人,北京師范大學物理學系2014級本科生.
[責任編輯:郭 偉]

