Matlab 在幾何光學(xué)仿真實(shí)驗(yàn)中的應(yīng)用
秦 華, 馮東太
(山東理工大學(xué) 理學(xué)院,山東 淄博 255049)
普通物理實(shí)驗(yàn)
Matlab在幾何光學(xué)仿真實(shí)驗(yàn)中的應(yīng)用
秦 華, 馮東太
(山東理工大學(xué) 理學(xué)院,山東 淄博 255049)
在工程光學(xué)教學(xué)中,為了使學(xué)生更好地理解球面光學(xué)成像系統(tǒng)與理想光學(xué)成像系統(tǒng)的區(qū)別,提出了用Matlab程序模擬球面光學(xué)系統(tǒng)成像過程的仿真實(shí)驗(yàn),并編制了模擬程序. 把系統(tǒng)結(jié)構(gòu)參量r,d,n和物距L等代入到模擬程序中,就可以仿真成像系統(tǒng)的成像過程. 仿真實(shí)驗(yàn)結(jié)果顯示:理想光學(xué)成像系統(tǒng)的成像性質(zhì)在球面光學(xué)成像系統(tǒng)中不存在,但可以通過設(shè)計(jì)優(yōu)化使球面系統(tǒng)近似達(dá)到或者無(wú)限接近理想成像系統(tǒng),理想成像系統(tǒng)的意義在于它的標(biāo)準(zhǔn)性.
幾何光學(xué);理想光學(xué)成像系統(tǒng);球面光學(xué)成像系統(tǒng);計(jì)算機(jī)仿真
研究光學(xué)系統(tǒng)的成像問題是幾何光學(xué)的主要內(nèi)容, 目前所使用的成像系統(tǒng)一般是球面鏡成像系統(tǒng),也有的在球面系統(tǒng)中加入1~2個(gè)非球面[1-2],還有一些加入部分二元光學(xué)元件[3],這些都還是以球面成像系統(tǒng)為基礎(chǔ).
在工程光學(xué)教學(xué)中,德國(guó)科學(xué)家高斯在1841年提出了理想光學(xué)系統(tǒng)的概念. 實(shí)際中除平面反射鏡外不存在真正的理想光學(xué)系統(tǒng),但平面反射鏡的垂軸放大率是1且成虛像,不適用于成像記錄. 理想光學(xué)系統(tǒng)中把光離散成光線,變成了純粹的幾何理論. 在工程光學(xué)教材中[4], 理想光學(xué)系統(tǒng)有下列3條重要性質(zhì):
1)光學(xué)系統(tǒng)物方1個(gè)點(diǎn)(物點(diǎn))對(duì)應(yīng)像方1個(gè)點(diǎn)(像點(diǎn)),即從物點(diǎn)發(fā)出的所有入射光線經(jīng)光學(xué)系統(tǒng)后,出射光線均交于像點(diǎn).
2)物方每條直線對(duì)應(yīng)像方的1條直線,稱共軛線;物方每個(gè)平面對(duì)應(yīng)像方的1個(gè)平面,稱為共軛面;任何垂直于主光軸的平面,其共軛面仍與主光軸垂直.
3)對(duì)垂直于主光軸的共軛平面,垂軸放大率為常量.
這3條性質(zhì)對(duì)于球面光學(xué)系統(tǒng)遠(yuǎn)軸光束不成立,或者只能近似成立. 由于學(xué)生還沒有接觸到光學(xué)設(shè)計(jì),對(duì)此學(xué)生很難理解,教師在課堂上也不容易講明,對(duì)此可以使用光學(xué)CAD來(lái)演示講解這個(gè)問題. 但是光學(xué)CAD都是商業(yè)軟件,使用需要一定的基礎(chǔ),再者即使會(huì)使用也無(wú)法展示其產(chǎn)生現(xiàn)象的原因. 而Matlab作為一種高級(jí)編程語(yǔ)言,由于其語(yǔ)法規(guī)則簡(jiǎn)單,貼近于人的思維方式,具有建模和仿真等諸多強(qiáng)大功能[5],因此可以引入到工程光學(xué)實(shí)驗(yàn)教學(xué)課堂中,讓學(xué)生自己編程仿真光線在光學(xué)系統(tǒng)中的傳播過程,通過仿真結(jié)果理解理想光學(xué)系統(tǒng)的3條性質(zhì),從而知道這3條性質(zhì)的意義就是作為一種設(shè)計(jì)標(biāo)準(zhǔn)而存在.
1 實(shí)際光線的光路計(jì)算及仿真
單個(gè)折射面的光路公式為[4]
(1)
式中,I和I′分別是入射角和折射角,n和n′是折射面兩側(cè)介質(zhì)折射率,r是球面的曲率半徑. 由式(1)可知,若物方截距L和物方孔徑角U已知,可以求得像方截距L′和像方孔徑角U′. 式(1)由折射定律和幾何三角關(guān)系得到,屬于實(shí)際光路的計(jì)算公式,是正確的,所以根據(jù)式(1)所編仿真程序的仿真結(jié)果也是正確的. 若有多個(gè)折射面,可迭次用式(1)和前后面的過渡公式(2)逐面計(jì)算.
(2)
因此可以用式(1)和(2)逐個(gè)驗(yàn)證理想光學(xué)系統(tǒng)的3條性質(zhì). 為此開設(shè)了仿真實(shí)驗(yàn)課,讓學(xué)生自己編寫Matlab仿真程序,模擬光束在光學(xué)系統(tǒng)中的傳播過程.
1.1 光學(xué)系統(tǒng)物方1個(gè)點(diǎn)(物點(diǎn))對(duì)應(yīng)像方1個(gè)點(diǎn)(像點(diǎn))的模擬證偽
表1列出了其雙膠合物鏡的結(jié)構(gòu)參量,選擇物距l(xiāng)=-75 mm,數(shù)值孔徑sinUmax=0.105,入瞳距l(xiāng)z=0,物高y=-7 mm.
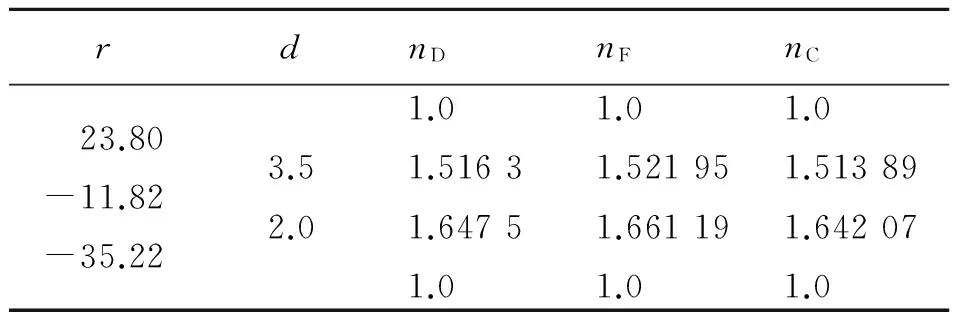
表1 物點(diǎn)對(duì)應(yīng)像點(diǎn)的模擬結(jié)構(gòu)參量
根據(jù)式(1)和(2)用Matlab語(yǔ)言編制光從物點(diǎn)經(jīng)過物鏡到像點(diǎn)的光線傳輸程序如下:
r=[23.8,-11.82,-35.22];
n=[1.0,1.5163,1.6475,1.0];
L(1)=-75;d=[3.5,2.0];
k=length(r)
for m=1∶k
n′(m)=n(m+1);
I(m)= asin((L(m)-r(m))*sin(U(m))/r(m));
h(m)=r(m)*sin(U(m)+I(m));
I′(m)=asin(n(m)/n′(m)*sin(I(m)));
U′(m)=U(m)+I(m)- I′(m);
L′(m)=r(m)*(1+sin(I′(m))/sin(U′(m)));
x(m)= L′(m)- r(m)*cos( I′(m)+ U′(m));
y(m)= r(m)*sin( I′(m)+ U′(m));
if m==1
dist=0;
else
dist=d(m-1);
end
b=dist+b;
if m==k
break
end
U(m+1)= U′(m);
L(m+1)=L′(m)-d(m);
end
plot(x,y)
此程序比較簡(jiǎn)單,通過引導(dǎo),大部分學(xué)生都會(huì)編寫,其中的意義也比較容易理解,所以通過程序的運(yùn)行,學(xué)生肯定對(duì)于“理想光學(xué)系統(tǒng)物方1個(gè)點(diǎn)(物點(diǎn))對(duì)應(yīng)像方1個(gè)點(diǎn)(像點(diǎn))”這條性質(zhì)的理想性有深刻的理解. 圖1 是以上程序的運(yùn)行結(jié)果,從圖中可以看出,物平面上的3點(diǎn)只有中間物點(diǎn)近似對(duì)應(yīng)1個(gè)像點(diǎn),其余兩物點(diǎn)經(jīng)過物鏡后變?yōu)樯撸f明這個(gè)物鏡不是理想成像系統(tǒng). 要想成為或者近似成為理想成像系統(tǒng)必須對(duì)系統(tǒng)進(jìn)行優(yōu)化設(shè)計(jì),才能在一定成像范圍內(nèi)近似達(dá)到“理想光學(xué)系統(tǒng)物方1個(gè)點(diǎn)對(duì)應(yīng)像方1個(gè)點(diǎn)”,這屬于光學(xué)設(shè)計(jì)范疇,在此不予贅述.
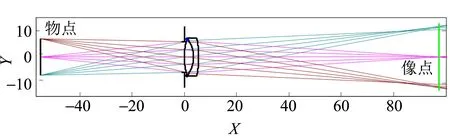
圖1 物點(diǎn)對(duì)應(yīng)像的仿真模擬
1.2 物方每條直線對(duì)應(yīng)像方的1條直線,稱共軛線的模擬證偽
表2給出了另一光學(xué)系統(tǒng)的結(jié)構(gòu)參量,選擇物距l(xiāng)=-1 mm,物空間數(shù)值孔徑sinUmax=0.100 305 6,孔徑光闌位置位于第4面頂點(diǎn),物高y=-3.5 mm. 在物面上取3個(gè)點(diǎn)A,B和C,A是軸上點(diǎn),B和C是軸外的2個(gè)物點(diǎn),同樣可以根據(jù)式(1)和(2)編程模擬A,B和C3個(gè)點(diǎn)發(fā)出的光經(jīng)過此光學(xué)系統(tǒng)后的成像情況,模擬結(jié)果如圖2所示. 從圖2可以看出,A,B,C3個(gè)點(diǎn)的像點(diǎn)分別為A′,B′,C′,在物空間ABC成1條垂軸直線,但ABC的像A′B′C′與光軸不再垂直,也不在1條直線上,說明“物方每條直線對(duì)應(yīng)像方的1

圖2 物距有限遠(yuǎn)時(shí)共軛線的仿真模擬
條直線”對(duì)于一般光學(xué)系統(tǒng)的不真實(shí)性. 由于以上系統(tǒng)中物方每條直線成像后并不是1條直線,所以也談不上“物方每個(gè)平面對(duì)應(yīng)像方的1個(gè)平面”. 從圖2所示的現(xiàn)象可以引出像場(chǎng)彎曲的概念,也就是像差理論中的場(chǎng)曲,為工程光學(xué)后章節(jié)像差理論的學(xué)習(xí)打下基礎(chǔ).
從以上分析中還可以引導(dǎo)學(xué)生理解理想光學(xué)系統(tǒng)的重要性. 如果不是理想光學(xué)系統(tǒng),所成的像就要變形,變形后像就失去了存在的意義,這樣的光學(xué)系統(tǒng)在市場(chǎng)就失去了競(jìng)爭(zhēng)力.
圖3是一成像物鏡對(duì)于無(wú)窮遠(yuǎn)處的物成像模擬光路圖. 從圖3中可以看出,對(duì)于無(wú)窮遠(yuǎn)處軸上物點(diǎn)發(fā)出的11條光線,經(jīng)過光學(xué)系統(tǒng)后還能很好地聚焦在一點(diǎn)(像點(diǎn)),但是對(duì)于無(wú)窮遠(yuǎn)處軸外物點(diǎn)發(fā)出的11條光線,經(jīng)過光學(xué)系統(tǒng)后只能近似地聚焦在一點(diǎn)(像點(diǎn)),并且這個(gè)軸外像點(diǎn)與軸上像點(diǎn)不在同一條垂軸線上,即垂直于主光軸的直線成像后不再垂直于主光軸,像場(chǎng)也發(fā)生了彎曲. 這與理想光學(xué)系統(tǒng) “任何垂直于主光軸的平面,其共軛面仍與主光軸垂直” 的性質(zhì)明顯不符.
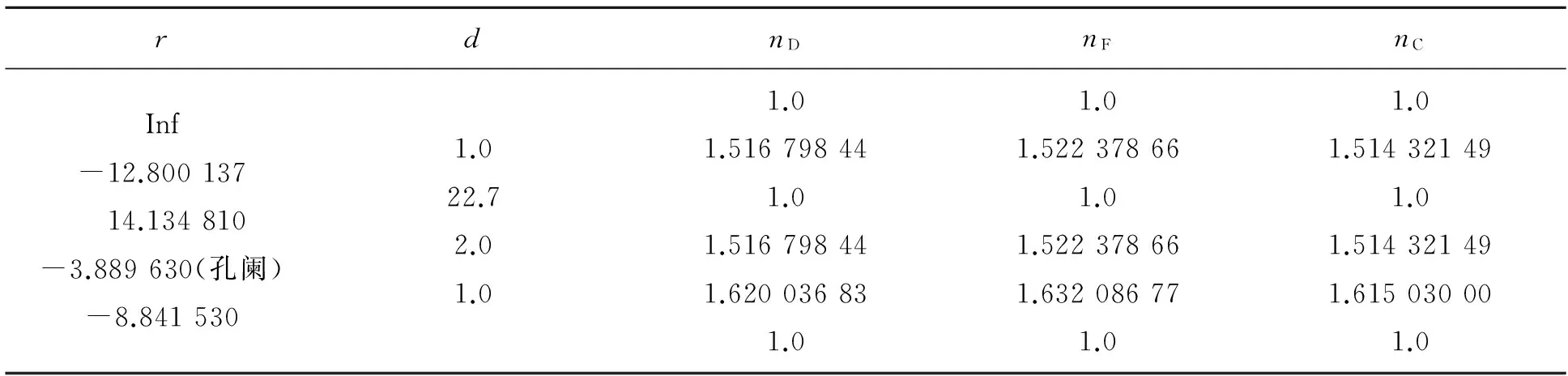
表2 共軛線的模擬結(jié)構(gòu)參量

圖3 物距無(wú)窮遠(yuǎn)時(shí)光學(xué)系統(tǒng)的成像模擬
為了達(dá)到或近似達(dá)到理想光學(xué)系統(tǒng)所具有的性質(zhì)“物方每條直線對(duì)應(yīng)像方的1條直線,任何垂直于主光軸的平面,其共軛面仍與主光軸垂直”,就必須對(duì)該光學(xué)系統(tǒng)的結(jié)構(gòu)參量r,d,n進(jìn)行調(diào)整優(yōu)化. 優(yōu)化的方法很多,現(xiàn)在光學(xué)設(shè)計(jì)最常用的是最小二乘法,如ZEMAX,CODEV,OSLO等,文獻(xiàn)[6-7]用粒子群算法進(jìn)行光學(xué)系統(tǒng)結(jié)構(gòu)優(yōu)化和設(shè)計(jì),取得了理想的效果. 由于本科生剛剛接觸到工程光學(xué),對(duì)像差理論還不了解,所以還不能進(jìn)行光學(xué)系統(tǒng)設(shè)計(jì)和優(yōu)化, 教師可以直接把優(yōu)化
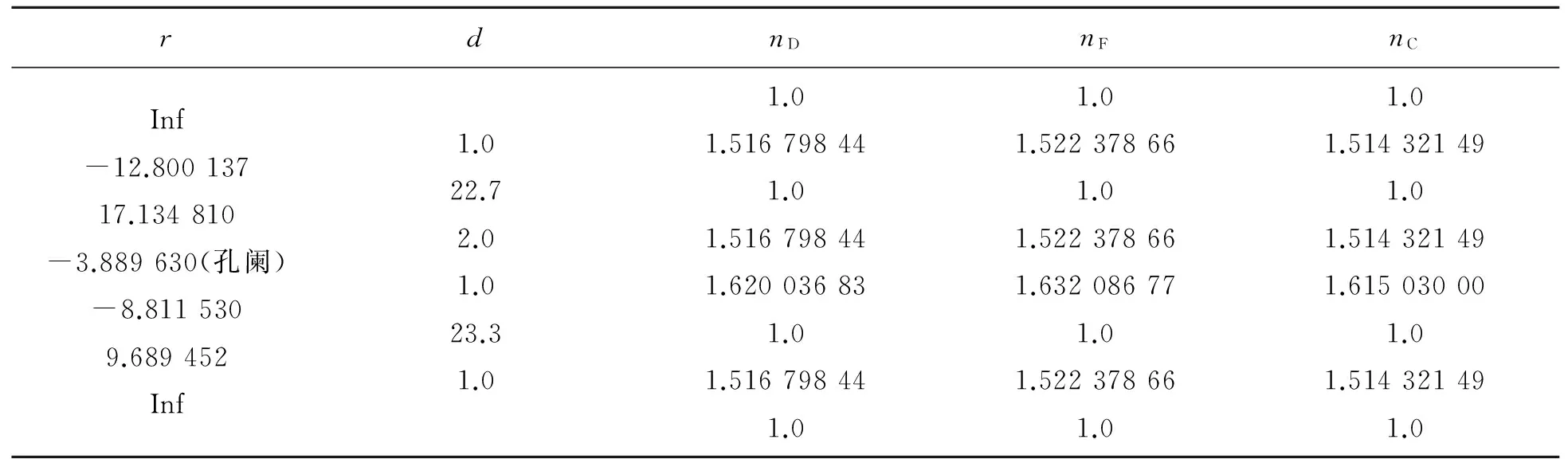
表3 優(yōu)化共軛線的模擬結(jié)構(gòu)參量
結(jié)果提供給學(xué)生,讓學(xué)生由優(yōu)化得到的系統(tǒng)結(jié)構(gòu)參量進(jìn)行光學(xué)模擬,從模擬結(jié)果對(duì)比優(yōu)化前后的不同. 表3給出了在表2所給結(jié)構(gòu)的基礎(chǔ)上進(jìn)一步消除場(chǎng)曲的新結(jié)構(gòu)參量,物距l(xiāng)=-1 mm,物空間數(shù)值孔徑sinUmax=0.100 005 6,孔徑光闌位置位于第4面頂點(diǎn),物高y=-2.5 mm. 圖4是由表3中結(jié)構(gòu)參量模擬得到的二維光路圖,從中可以看出垂直于光軸的物AB經(jīng)此光學(xué)系統(tǒng)后像A′B′近似垂直于光軸,說明表3中的光學(xué)系統(tǒng)在一定成像范圍內(nèi)近似滿足理想光學(xué)系統(tǒng)“物方每條直線對(duì)應(yīng)像方的1條直線”的性質(zhì). 從這里也可以引導(dǎo)學(xué)生懂得學(xué)習(xí)工程光學(xué)的最終目的是培養(yǎng)光學(xué)設(shè)計(jì)工程師,研究光學(xué)設(shè)計(jì)的方法,使所設(shè)
計(jì)的成像系統(tǒng)無(wú)限接近理想成像系統(tǒng).
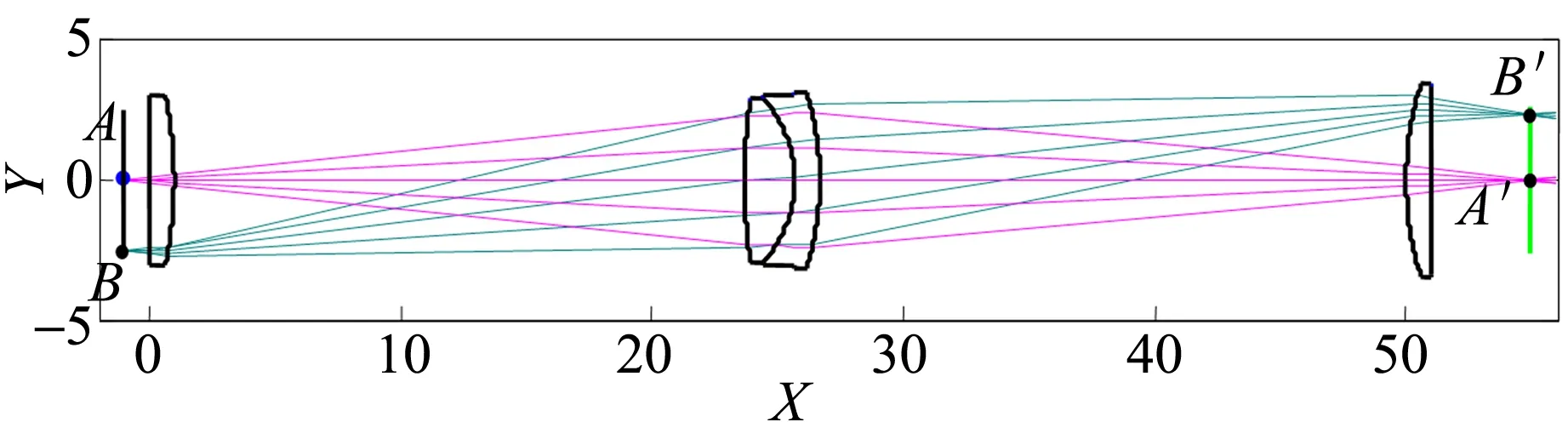
圖4 優(yōu)化后的共軛線的仿真模擬
1.3 對(duì)垂直于主光軸的共軛平面,垂軸放大率為常量的模擬證偽
表4列出了由ZEBASE庫(kù)中搜到一光學(xué)系統(tǒng)的結(jié)構(gòu)參量,物距l(xiāng)=-315.189 9 mm,物空間數(shù)值孔徑sinUmax=0.019 628 58,孔徑光闌表4中已給出,成像最大物高y=-80 mm.
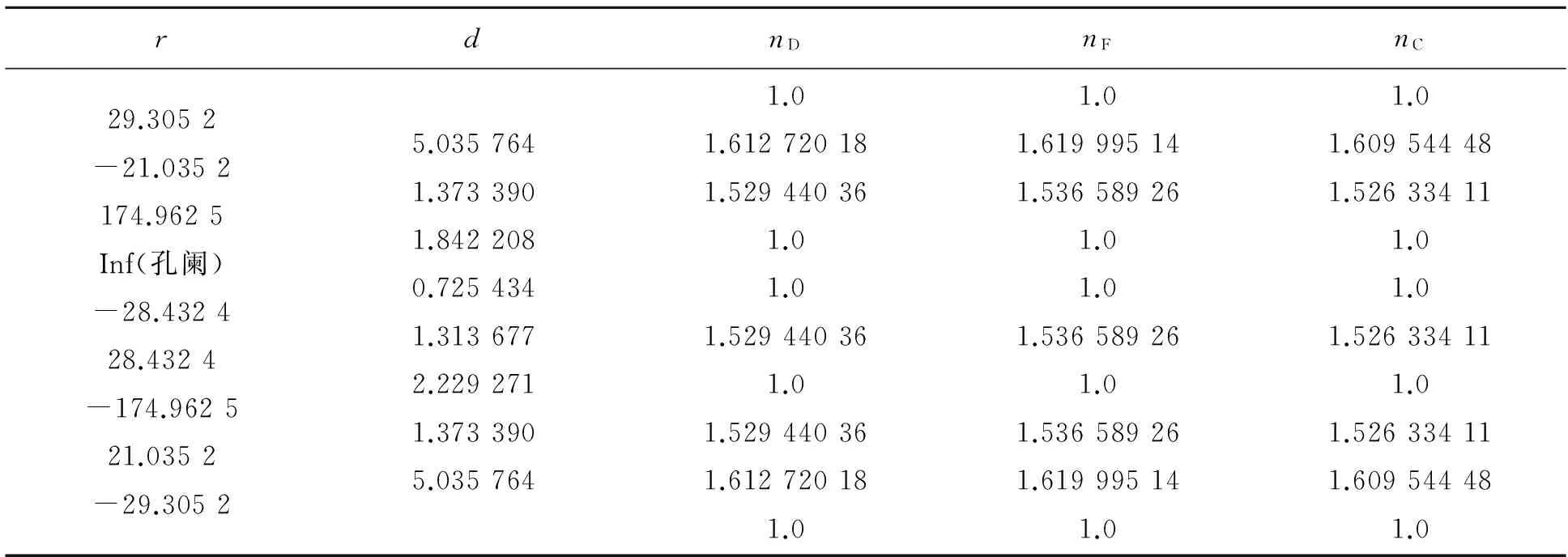
表4 由ZEBASE庫(kù)中得到的共軛面模擬結(jié)構(gòu)參量


顯然,β1≠β2,說明系統(tǒng)垂軸放大率并不是常數(shù),此系統(tǒng)不是理想系統(tǒng),但就其垂軸放大率來(lái)講已經(jīng)非常接近理想光學(xué)系統(tǒng). 使垂軸放大率是一常數(shù),達(dá)到理想成像系統(tǒng),是光學(xué)設(shè)計(jì)工作者一項(xiàng)重要的研究?jī)?nèi)容.

圖5 共軛面的仿真模擬
2 討 論
目前只有平面鏡能達(dá)到理想光學(xué)系統(tǒng)的要求,但平面鏡的放大率為1,所成的像為虛像,因此不適用于記錄真實(shí)世界. 現(xiàn)在常用的光學(xué)成像系統(tǒng)大多是球面成像系統(tǒng),對(duì)于球面成像系統(tǒng)與理想成像系統(tǒng)的區(qū)別,學(xué)生很難理解,認(rèn)為工程光學(xué)中所講的理想光學(xué)成像系統(tǒng)的成像公式是任何光學(xué)成像系統(tǒng)都適用的,這種誤解導(dǎo)致了工程光學(xué)學(xué)習(xí)中概念的混亂. 本文根據(jù)幾何光學(xué)理論,從學(xué)生熟知的球面折射公式出發(fā),使用Matlab語(yǔ)言編程仿真了球面光學(xué)系統(tǒng)成像過程,由仿真結(jié)果證實(shí)理想光學(xué)系統(tǒng)所具有的性質(zhì)對(duì)于球面光學(xué)系統(tǒng)是不存在的,起碼不能同時(shí)存在,通過優(yōu)化設(shè)計(jì),球面成像系統(tǒng)可以近似達(dá)到或者接近理想成像系統(tǒng),但不會(huì)完全達(dá)到理想成像系統(tǒng).
3 結(jié)束語(yǔ)
通過本文的仿真實(shí)驗(yàn),不但可以使學(xué)生更好地理解了工程光學(xué)中理想光學(xué)系統(tǒng)的概念和性質(zhì),還使學(xué)生學(xué)會(huì)了使用Matlab語(yǔ)言編程,增強(qiáng)了學(xué)生學(xué)習(xí)興趣,拓展了學(xué)生的知識(shí)面,達(dá)到了事半功倍的效果. 本文的仿真實(shí)驗(yàn)還為像差理論的
學(xué)習(xí)打下了基礎(chǔ),也使學(xué)生提前接觸到光學(xué)設(shè)計(jì)的內(nèi)容,使學(xué)生對(duì)于工程光學(xué)這門課有了更全面深刻的理解.
[1] Hou J, Li H, Wu R, et al. Method to design two aspheric surfaces for imaging system [J]. Appl. Opt.,2013,52(11):2294-9.
[2] Miks A, Novak J, Novak P. Third-order design of aspheric spectacle lenses [J]. Optik-International Journal for Light and Electron Optics,2010,121(23):2097-2104.
[3] 韓雪冰,劉華,張文靜,等. 二元光學(xué)元件在微光夜視物鏡中的應(yīng)用研究[J]. 長(zhǎng)春理工大學(xué)學(xué)報(bào), 2013,36(1/2):20-23.
[4] 郁道銀,談恒英. 工程光學(xué)[M]. 3版. 北京:機(jī)械工業(yè)出版社,2011.
[5] 何鈺,吳平,張曉,等. Matlab在物理學(xué)中的應(yīng)用[J]. 大學(xué)物理,2013,32(12):39-42.
[6] Qin H. Aberration correction of a single aspheric lens with particle swarm algorithm [J]. Optics Communications, 2012,285(13/14):2996-3000.
[7] Qin H. Particle swarm optimization applied to automatic lens design [J]. Optics Communications, 2011,284(12):2763-2766.
ApplicationofMatlabinsimulatedgeometricalopticsexperiments
QIN Hua, FENG Dong-tai
(School of Sciences, Shandong University of Technology, Zibo 255049, China)
When teaching of engineering optics, in order to enable students to better understand the difference between a spherical optical imaging system and an ideal optical imaging system, a simulation experiment using Matlab was presented. Structural parametersr,d,nandL(object distance) of an optical system were substituted into emulation programs, the imaging process of a spherical optical system could be emulated. The simulation results showed that the imaging properties of ideal optical imaging system did not exist in spherical optical imaging systems, however, spherical systems could approximately approach or infinitely close to the ideal imaging system by optimizing the design of the structure. The worth of an ideal imaging system lied in its standards.
geometrical optics; ideal imaging system; spherical optical imaging system; computer simulation
O4-39
A
1005-4642(2017)11-0013-05

2017-01-23
山東省自然科學(xué)基金資助(No.ZR2012FM001)
秦 華(1964-),男,山東臨沂人,山東理工大學(xué)理學(xué)院副教授,博士,主要從事光學(xué)設(shè)計(jì)、全固態(tài)激光器及透明導(dǎo)電薄膜方面的研究工作.
馮東太(1961-),男,山東淄博人,山東理工大學(xué)理學(xué)院教授,博士,主要從事量子光學(xué)與量子信息方向的工作.
[責(zé)任編輯:尹冬梅]

