我國糧食種植面積模型構建及研究

(國防科技大學 湖南 長沙 410000)

我國糧食種植面積模型構建及研究

楊文堯

(國防科技大學湖南長沙410000)

糧食不僅是人們日常生活的必需食品，而且還是維護國家經濟發展和政治穩定的戰略物資，具有不可替代的特性。而糧食種植面積是影響糧食產量的直接原因，因此，研究影響糧食種植面積的因素對糧食政策的制定有著重要的指導意義。影響糧食種植面積的因素比較多，它們之間的關系錯綜復雜而且可能存在著糧食品種和區域差異。本文通過分析影響糧食種植面積的指標和關于糧食種植面積的數學模型，討論、評價指標的合理性，并研究它們之間的關系，并對得出的相應結果的可信度和可靠性給出檢驗和分析。

種植面積；模型；評價指標

一、影響糧食種植面積的指標分析

文章選取山東省2005-2014年的小麥種植面積，統計數據源于國家統計局，見附件。文章通過查閱資料，整理影響糧食種植面積的因素如表1中第一列所示。然而，在數據分析的過程中，影響糧食種植面積的指標不一定是可測的，因此需要將指標轉換為可測變量，如表1中第二列所示。

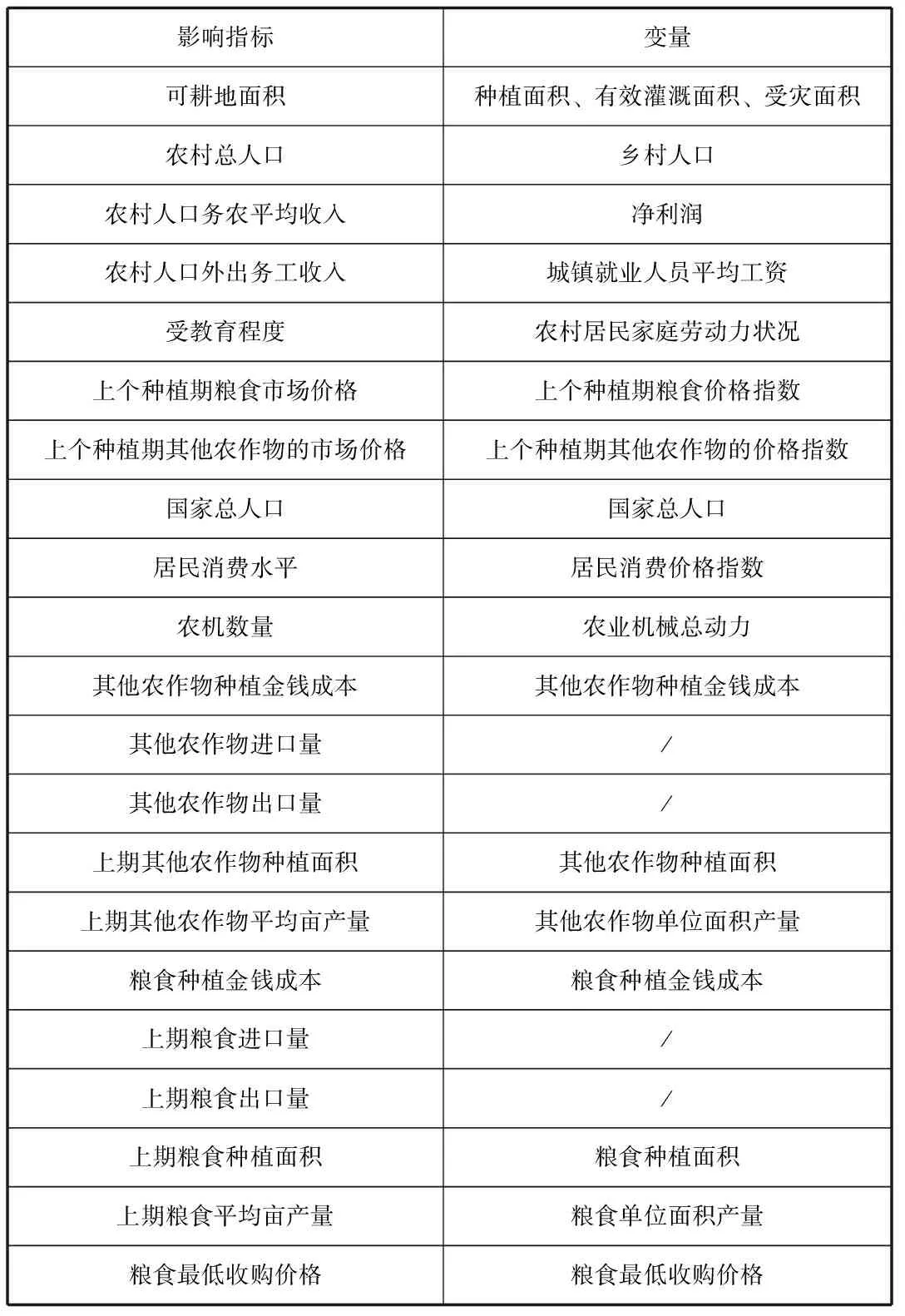
表1 影響糧食種植面積的指標以及轉化變量

二、指標變量相關性分析和主成分分析

(一)指標變量相關性分析

由于指標數量較多，指標之間的關系比較復雜，因此，首先對指標進行相關性分析，分析結果如圖1所示。

由圖11可以看出：(1)小麥單位面積產量、農業機械總動力、平均出售價格、小麥生茶價格指數、最低收購價、城鎮單位就業人員平均工資、居民消費水平和農村軍民家庭人均純收入與小麥種植面積之間的相關性較強；(2)雖然剩余的變量和小麥種植面積的相關性較低，但是在多元回歸分析中，自變量發生的作用不是獨立的，而是與其他自變量一起聯合發揮作用，每個自變量的影響都是在控制了其他自變量的基礎之上的分析。因此，如果一個自變量與因變量相關性較低，但它與其他自變量一起時，是可以對因變量產生顯著影響的，所以本文在回歸分析中依舊選入相關性不顯著的變量。

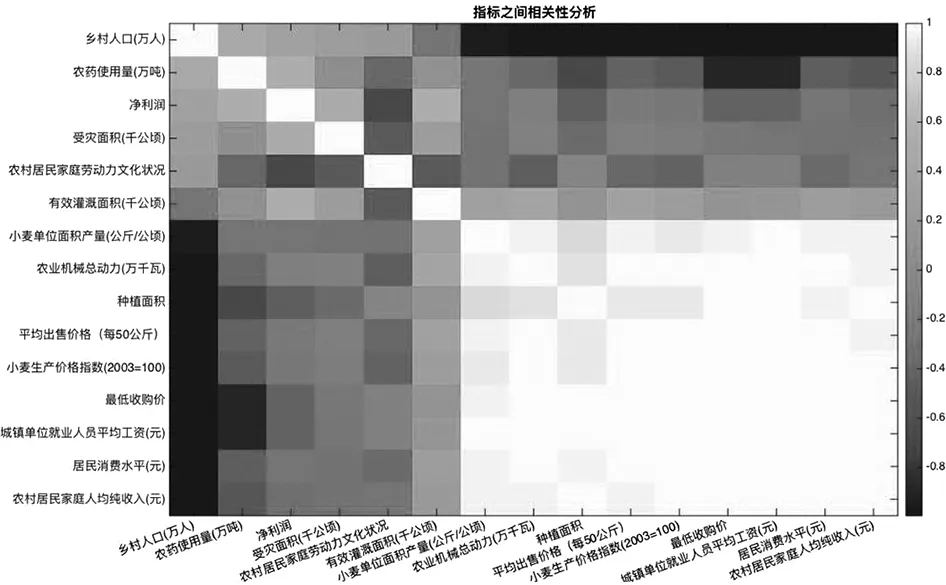
圖1 指標相關性分析圖

另一方面，當兩個變量之間的相關性很高，說明兩個變量之間存在完全線性關系。為了降低變量的維度，可從相關性很高的變量中選取具有代表性的變量進行回歸分析。在9個相關性很高的變量中，通過分析可以發現，一些變量之間是完全線性相關的，而且其內涵是類似的，可以對這些變量進行歸約，如表2所示。

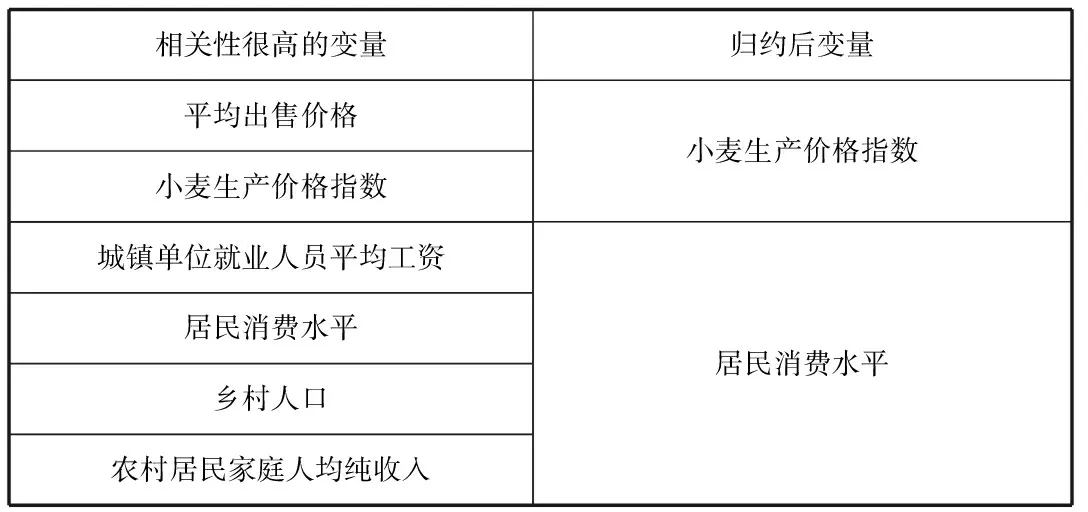
表2 變量規約

通過對變量進行刪除和歸約，得出最終作為自變量進入回歸分析的變量，如表3所示。

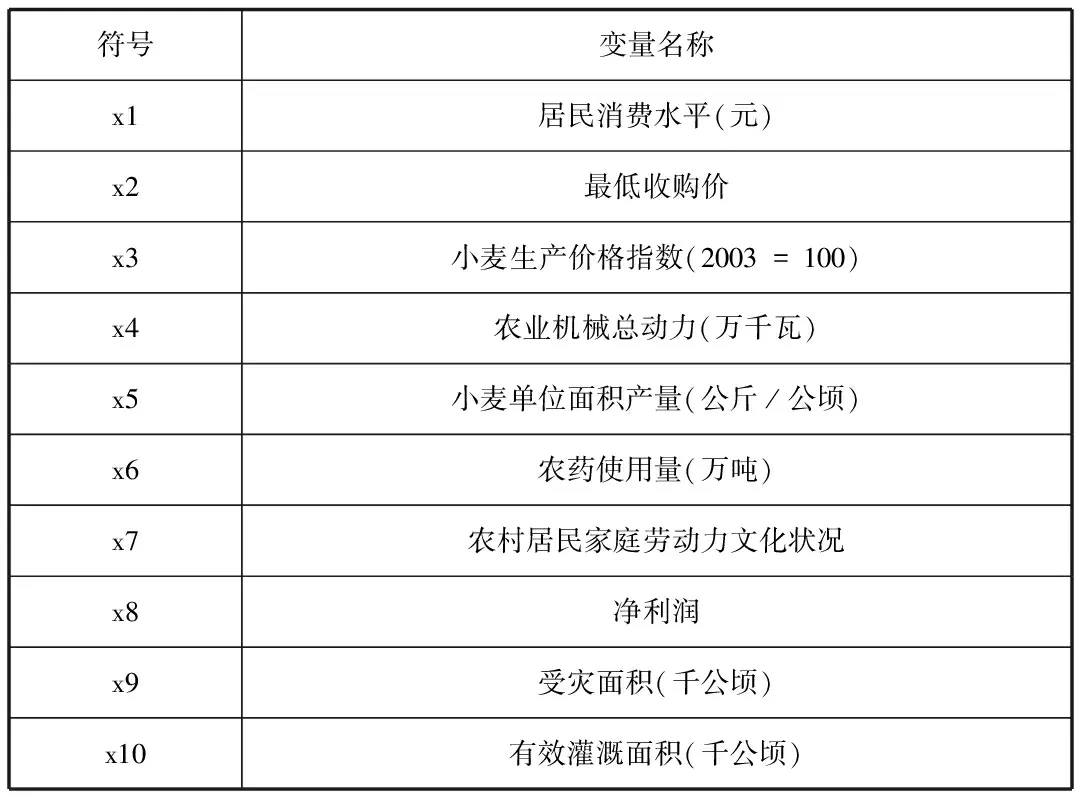
表3 最終變量選取

(二)指標變量主成分分析

主成分分析是利用降維的思想，在損失很少信息的前提下，設法將原來眾多具有一定相關性(比如P個指標)，重新組合成一組新的互相無關的綜合指標來代替原來的指標。

由于選取的變量數量依舊較多，且之間具有一定的相關性，因此，采用主成分分析法將相關的指標組合為一組不相關的主成分。首先，通過因子特征值確定主成分的個數，如圖3所示，本文將特征值gt;0.6的因子可作為主成分。

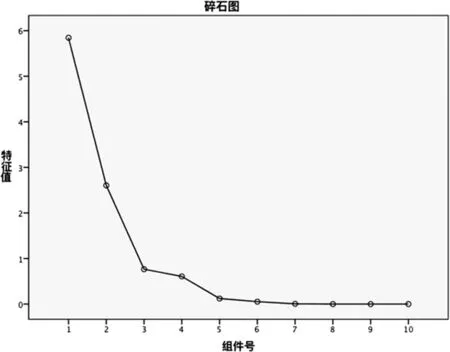
圖3 主成分分析—碎石圖

圖中橫坐標表示因子序號，縱坐標為因子對應的特征值，根據因子的特征值可確定是否作為主成分。根據圖3可以看出，因子1、2的特征值gt;0.6，說明因子1、2可作為主成分。進而繼續分別用y1、y2表示。

確定主成分個數之后，進而通過成分矩陣可以描述每個變量與主成分的相關程度，如表4所示。

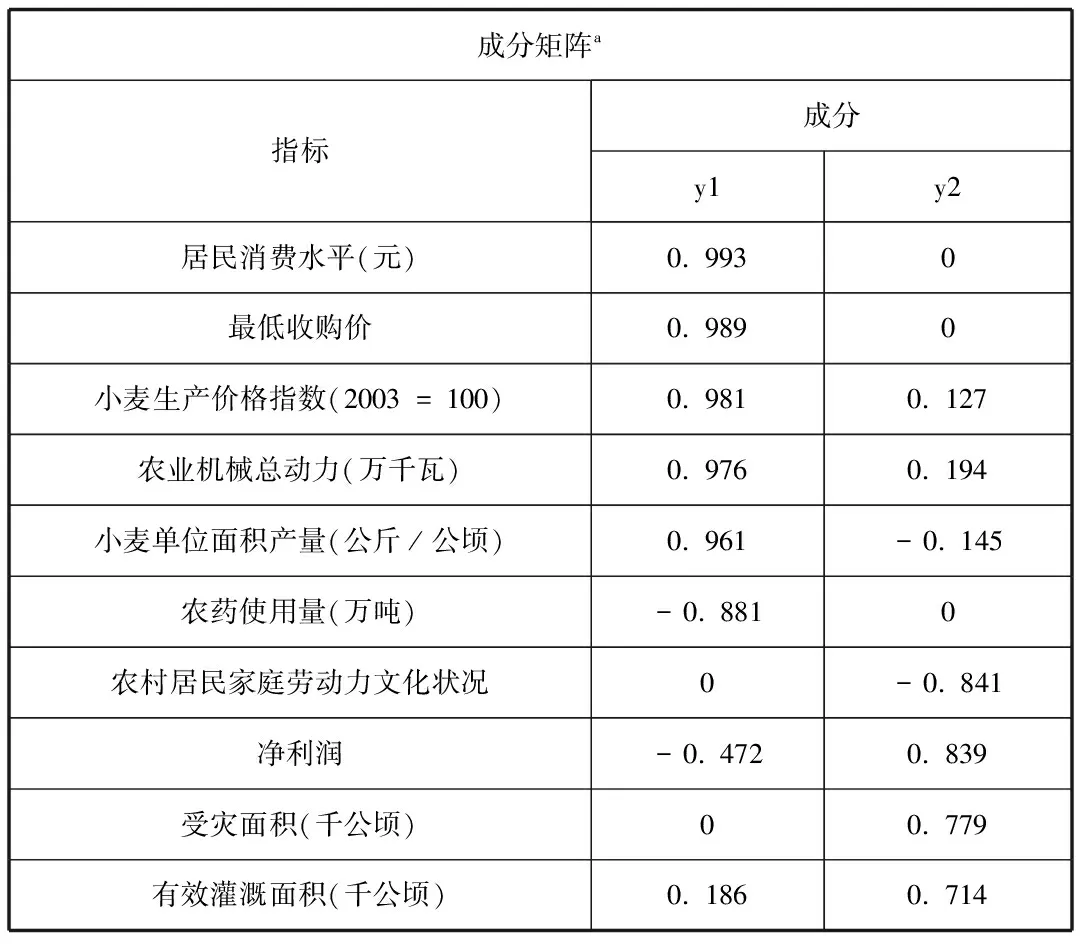
表4 指標與主成分的相關程度

圖5更加直觀地展示變量與主成分之間的影響關系。

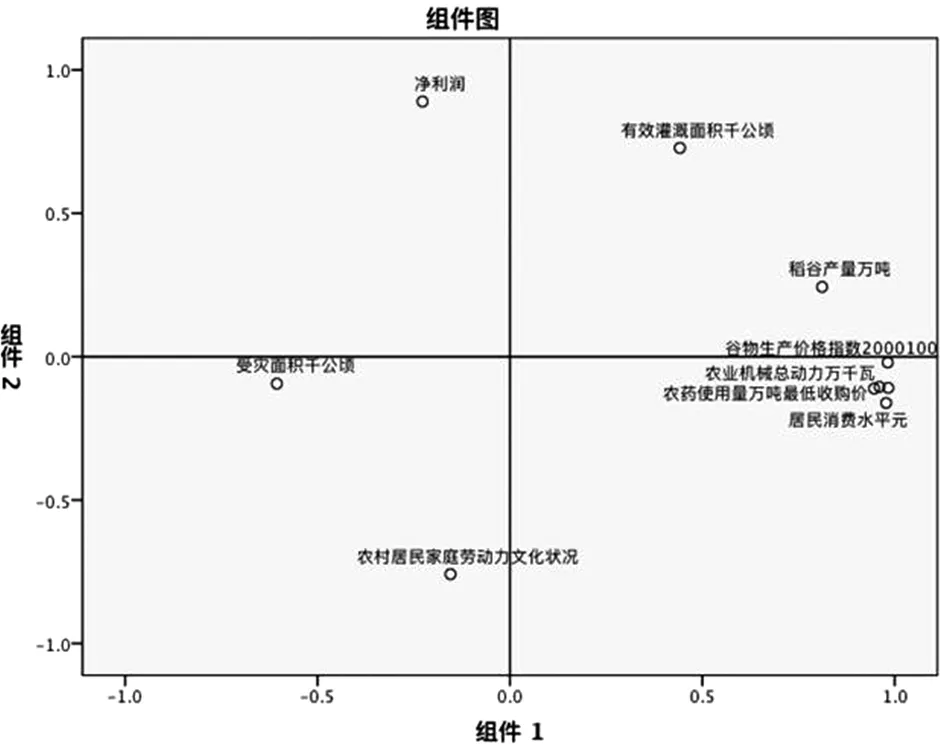
圖5 變量與主成分的相關程度

由表5和圖5可以看出：變量x1、x2、x3、x4、x5、x6和主成分y1之間相關性較強，x6和y1之間是負相關，其他是正相關；x7、x9、x10和主成分y2之間相關性較強，且x7和y2之間是負相關，其他為正相關；x4和兩個主成分都有一定的相關性。

僅僅獲取變量和主成分之間的相關性不足以描述它們之間的影響關系，通過成分得分系數矩陣，可以獲取指標在對應主成分中所占的比重系數，如表5所示。

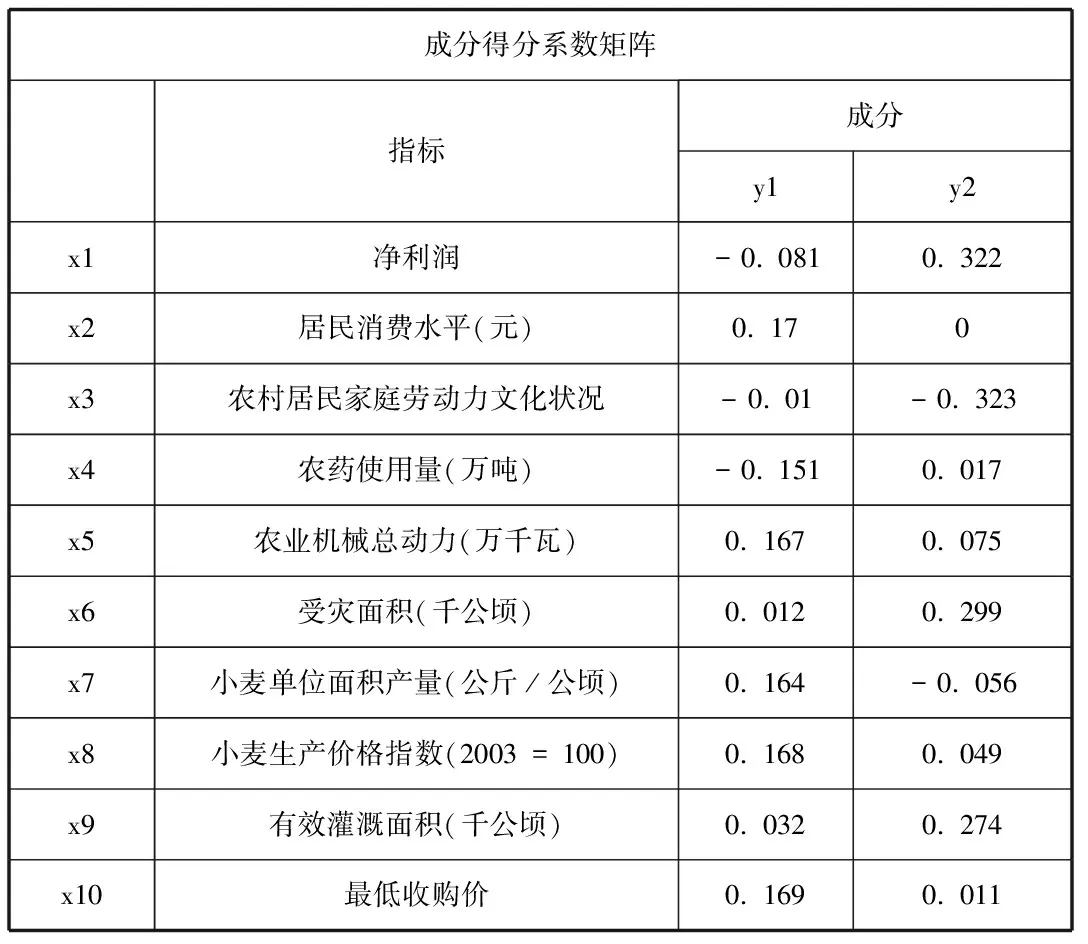
表5 成分得分系數表

根據表5，可以獲取變量和主成分之間的函數關系如下：

y1=-0.081x1+0.17x2-0.01x3-0.151x4+0.167x5+0.012x6+0.164x7+0.168x8+0.032x9+0.169x10

y2=0.322x1+0*x2-0.323x3+0.017x4+0.075x5+0.299x6-0.056x7+0.049x8+0.2740x9+0.011x10

三、回歸分析

回歸分析是研究一個因變量或多個因變量與一個自變量之間是否存在某種線性或非線性的關系，并確定自變量與因變量之間的回歸方程式。本文的因變量為小麥種植面積z1，自變量為主成分y1、y2，首先根據主成分對其進行回歸分析。

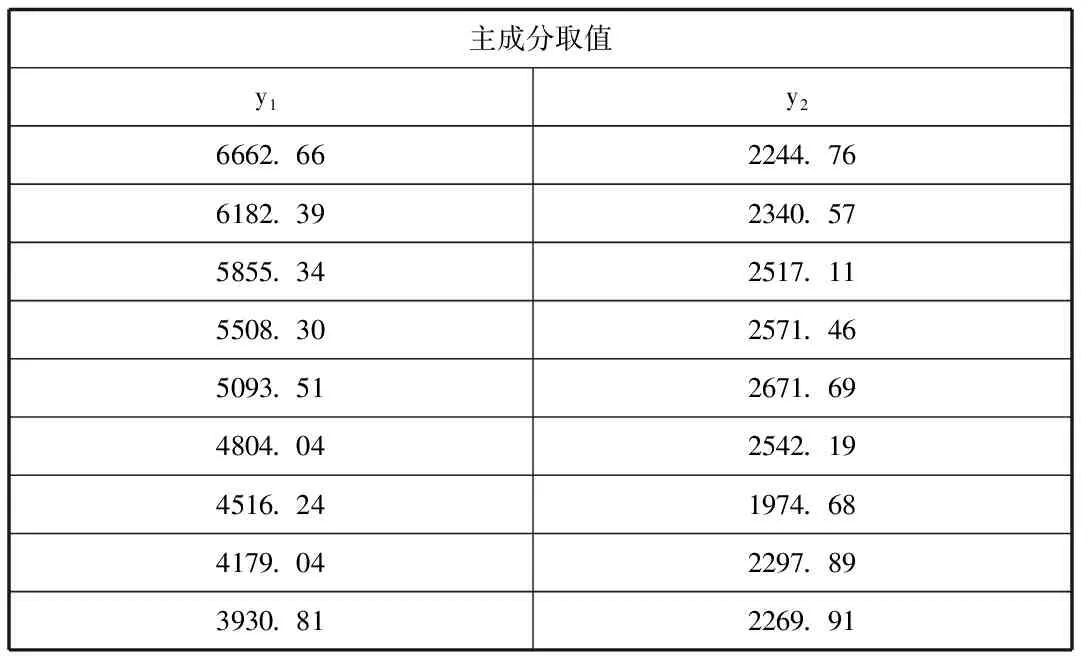
表6 主成分取值表

(一)確定回歸類型

首先對主成分y1、y2和種植面積z1進行偏相關分析，如圖6所示。

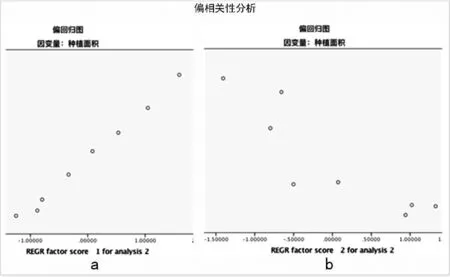
圖6 因變量和自變量之間的偏回歸圖

圖6中，a圖表示y1和z1之間的偏相關分析，b圖表示y2和z1之間的偏相關分析。由圖可知可知y1和z1之間是完全正線性相關的，y2和z1之間是近似負線性相關的。因此，適用于采用多元線性回歸的方式進行回歸分析。

(二)多元線性回歸分析

選取小麥種植面積為因變量z1，主成分y1、y2為自變量，采用步進的方法進行多元線性回歸分析，結果如表7所示。

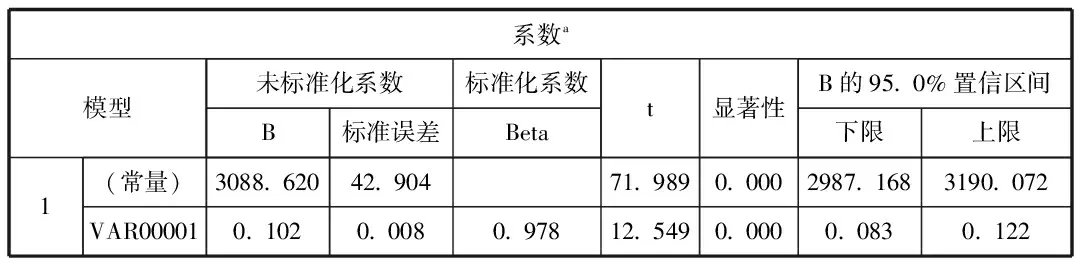
表7 多元線性回歸分析結果

由表可以看出，由于y2對種植面積的影響不顯著，在回歸模型中被自動消除，自變量y1的顯著性0，說明模型回歸效果良好，y1自變量可以有效預測因變量。根據表X的標準化系數，可確定影響糧食種植面積的多元線性回歸方程為：

=gt;z1=3088.62-0.0083x1+0.0173x2-0.001x3-0.0154x4+0.017x5+0.012x6+0.0167x7+0.0171x8-0.0033x9+0.0172x10

(三)回歸方程檢驗

為了驗證方程的合理性以及可靠性，進行模型擬合度、顯著性和適合性檢驗。

1.模型擬合度檢驗

擬合度是指回歸直線對觀測值的擬合程度，首先進行模型擬合度檢驗，結果如表8所示。

表8 擬合度檢驗

表中R稱為多元相關系數，R方代表著模型的擬合度，一般而言，兩者大于0.4即可，由表8可以看出該模型的擬合優度良好。

2.模型顯著性檢驗

首先進行所有自變量的回歸系數的一個總體檢驗，即F檢驗，如表9所示。

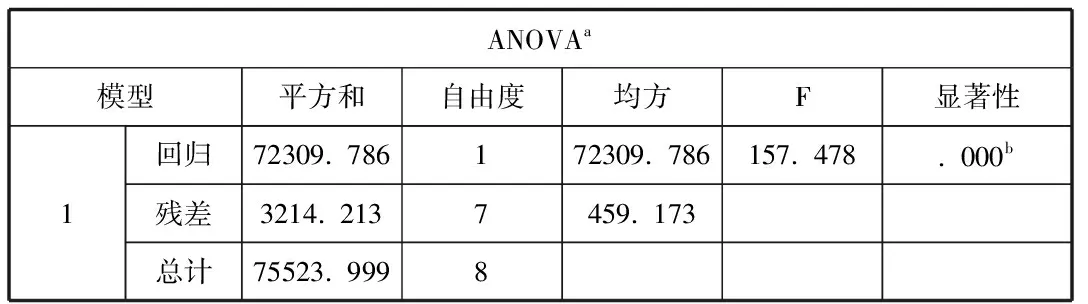
表9 回歸系數的檢驗

F的值較大，代表著該回歸模型是顯著的，由表可知，F的值足夠大，且顯著性小魚0.05，說明回歸模型總體上是顯著的。

3.模型適合性檢驗

模型適合性檢驗主要是進行殘差分析，如圖7所示。

圖7 標準化殘差圖

通過圖7，可以看出實測累計概率和預期累計概率基本上一致，說明模型滿足適合性。

[1]李岳云等著.中國糧食波動論[M].中國農業出版社,2001.

[2]黃益平,宋立剛著.應用數量經濟學[M].上海人民出版社,2001.

[3]婁峰,張濤.中國糧食價格變動的傳導機制研究——基于動態隨機一般均衡(DSGE)模型的實證分析[J].數量經濟技術經濟研究.2012(07).

[4]溫濤,王小華.財政金融支農政策對糧食價格波動的影響——基于中國1952-2009年的經驗驗證[J].東南大學學報(哲學社會科學版).2012(03).

[5]車巧怡.中國糧食產品進出口情況與國內糧食價格的相關性分析[J].吉林金融研究.2012(05).

[6]秦志勇,許建新.國內外糧食市場互動關系的局部均衡模型分析[J].重慶科技學院學報(社會科學版).2012(07).

[7]何蒲明,朱信凱.我國糧食價格波動與CPI關系的實證研究[J].農業技術經濟.2012(02).

[8]吳娟,王雅鵬.我國糧食儲備調控體系的現狀與完善對策[J].農業現代化研究.2011(06).

[9]高帆,龔芳.國際糧食價格的波動趨勢及內在機理:1961-2010年[J].經濟科學.2011(05).

楊文堯(1994.01-)，男，漢族，湖南臨澧人，研究生，國防科技大學，公共管理。