高強混凝土溫濕耦合應力計算與開裂風險分析

尤偉杰，王有志，張 雪，徐剛年，王世民

(山東大學 土建與水利學院，濟南 250000)

高強混凝土溫濕耦合應力計算與開裂風險分析

尤偉杰，王有志，張 雪，徐剛年，王世民

(山東大學 土建與水利學院，濟南 250000)

為揭示高強混凝土早齡期構件溫濕耦合影響下的應力變化規律與開裂風險，以混凝土棱柱體為例，建立了高強混凝土構件溫濕耦合計算方法和早齡期約束收縮應力計算方法，通過編程實現了溫濕度場的模擬.計算結果表明：建立的溫濕度耦合作用模型能夠較好預測高強混凝土1 d到28 d齡期溫濕度場的發展變化規律；在澆水養護條件下，溫濕度耦合效應對高強混凝土溫度場、濕度場和應力影響很小；停止養護后，約束應力和開裂風險快速增大.養護與環境溫濕度對高強混凝土早齡期應力變化和開裂風險影響顯著.

收縮徐變；溫濕耦合；約束應力；有限差分法；開裂風險

約80%的混凝土結構裂縫是由于溫度、濕度變化或自身因素作用下產生的非荷載應力造成的[1].混凝土早齡期變形為溫濕變形，且混凝土溫度場和濕度場的變化具有明顯的非線性特征.Bazant等[2]對混凝土早齡期溫度、濕度非線性特性進行了詳細試驗和理論研究，提出了考慮水分擴散和水泥水化耗水的混凝土內部濕度控制方程.混凝土的溫升、自干燥及干燥作用往往同時存在，且各因素之間相互聯系、相互影響，存在一種復雜的耦合作用[3].

混凝土構件內部濕度變化與其變形具有一定的相關關系.侯東偉[4]基于Kelvin方程，建立了考慮水化耗水和蒸發的收縮變形一體化計算模型，該模型考慮硅灰對混凝土早齡期飽和度的影響，但未考慮溫濕度的相互影響.在沒有外荷載影響的情況下，混凝土構件的應力來自周邊構件或結構對變形的約束.康明[5]推導了混凝土配筋構件在周邊約束下內部應力的量化計算模型.

本文基于水化度理論，考慮高強混凝土早齡期溫濕度的相互影響，建立了高強混凝土早齡期溫濕耦合模型，實現了高強混凝土棱柱體構件早齡期應變和溫濕度場的模擬計算，并與既有的試驗值進行對比.利用改進的計算模型對約束應力、溫濕耦合效應及開裂風險進行計算分析.

1 溫濕耦合模型

1.1 溫度控制方程

大量試驗研究結果表明，當相對濕度降到一個特定數值時(75%左右)，水化過程會減緩或者停止[6]，因此，引入系數β(H)=[1+(5-5H)4]-1來考慮相對濕度對水化作用的影響，建立溫度控制方程:

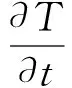
(1)

式中：ρ為混凝土密度，取值為2 370 kg/m3；c為混凝土比熱系數，取值17 J/(mm·h·℃)；T為攝氏溫度；k為混凝土傳熱系數，取值948.3 J/(kg·℃)；Q(T)為混凝土水化放熱項.

基于水化度理論[7]求解水化放熱速率為

(2)

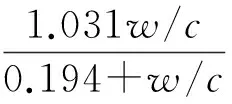
水化度的計算方法為[8]

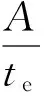
(3)

式中：te為混凝土的等效齡期,A和B為經驗常數.

等效齡期由下式確定[8]:

(4)

式中：R為理想氣體常數,Uar為參考溫度下的反應活化能,UaT為溫度T下的反應活化能.

Uar、UaT由下式確定[9]：

Uar=41 970exp (-0.003 4t)，

(5)

UaT=(42 830-43T)exp ((-0.000 17T)t).

(6)

綜上，混凝土水化熱放熱速率計算公式為

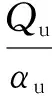
1.2 濕度控制方程

混凝土早齡期濕度控制方程為[2]

(7)

式中：H為相對濕度,D(H)為水分傳輸系數,Hd為混凝土蒸發擴散項,Hs為水化耗水項.

歐洲混凝土規范給出的傳輸系數D(H)的計算方法為

(8)

式中：Dmax為飽和狀態下的濕度擴散系數,Hc為濕度下降臨界值,β和θ為經驗系數.

式(8)關于D(H)的使用條件通常為恒溫狀態.如果溫度機制在擴散過程中占主導地位，那么溫度效應遵從速率過程理論[2]，基于這個假設可以給出溫度對擴散的影響系數[10]：

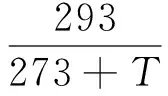
(9)

式中Ead為表觀活化能.

從而可以得到受溫度影響的混凝土擴散系數：

D(T,H)=f(T)D(H).

(10)

Oh等[11]提出了考慮水化度非線性變化的自干燥水化耗水計算模型：

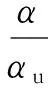
(11)

式中：Hs,u為最終水化度對應的水化反應引起的相對濕度變化,φ為經驗系數.

ZHANG等[9]以濕度飽和為臨界點，對上述水化耗水計算模型進行了修正：

(12)

式中αc為濕度飽和期結束時的水化度.

濕度場計算所需各參數的取值見表1.

1.3 溫濕度場的模擬

采用二維有限差分法，根據不同濕度分布和邊界條件可分解為內部、絕濕和非絕濕3種節點情況.

對于內部節點，可將式(1)進行Grank-Nicholson變換得到二階差分方程并變換為迭代形式:

(13)

(14)

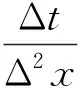
對于非絕濕節點可建立二階差分格式并變為迭代形式：

(15)

對于非絕溫節點可建立一階差分格式并變為迭代形式：

).

(16)

式中：Ha為與外表面接觸的環境相對濕度,am為混凝土表面水分擴散系數.

Yuan等[12]給出了表面節點水分傳輸系數的計算方法:

am=A(0.253+0.06va)(H-Ha).

(17)

式中：A為經驗系數,va為混凝土表面風速,Ha為外界環境相對濕度.溫度場的模擬與濕度場類似，不再具體說明.

1.4 濕度應變計算模型

侯東偉[4]根據Kelvin方程，在大量試驗和理論研究的基礎上[4,13-15]，建立了以相對濕度為主要變量的考慮水化耗水和蒸發的收縮變形一體化計算模型:

(18)

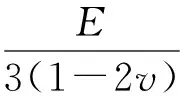
成熟混凝土只需要考慮混凝土飽和度與相對濕度之間的關系，因為其微觀孔結構相對穩定，但是早期混凝土中水化作用導致微孔結構不斷演變，直接影響到其熱濕傳輸過程[17].

DU等[18]建立了混凝土水化度、溫度、濕度與飽和度的關系：

(19)

式中：m、n為材料參數,γ為液體表面張力系數.

彈性模量是混凝土早齡期應力應變的重要影響參數，本文采用基于水化度理論彈性模量的計算方法[19]：

(20)

式中：E28為28 d彈性模量,α0為水泥凝結時的水化度,b為經驗系數.

濕度變形計算所需各參數的取值見表2.

表2 濕度變形計算參數取值

2 約束應力計算

2.1 約束應力計算模型

混凝土構件早齡期變形會受到內部鋼筋和骨料以及周邊相鄰構件的約束而產生約束應力，當約束應力超過混凝土抗拉強度則會導致構件開裂.圖1為工程中常見的一種受約束混凝土構件形式.

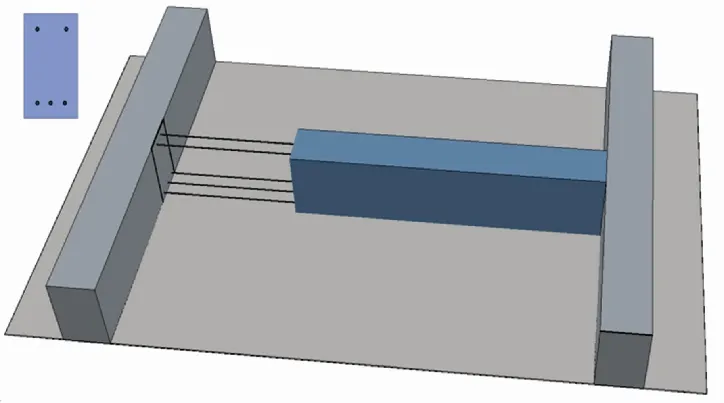
圖1 計算模型橫截面

以此構件為例，可建立計算模型.基本假設為：1)混凝土為各向同性材料；2)濕度分布沿梁的長度方向不變；3)接觸不發生濕度交換；4)鋼筋和混凝土之間沒有相對滑移；5)構件底部不受摩擦力等約束限制.根據混凝土構件受到的約束特點，建立圖2的計算模型.

康明[5]將端部約束看成彈簧系統，根據位移平衡條件和力平衡條件得到混凝土的應力增量:

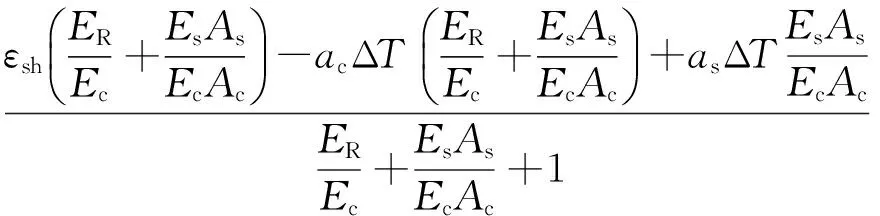
(21)

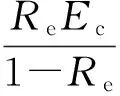
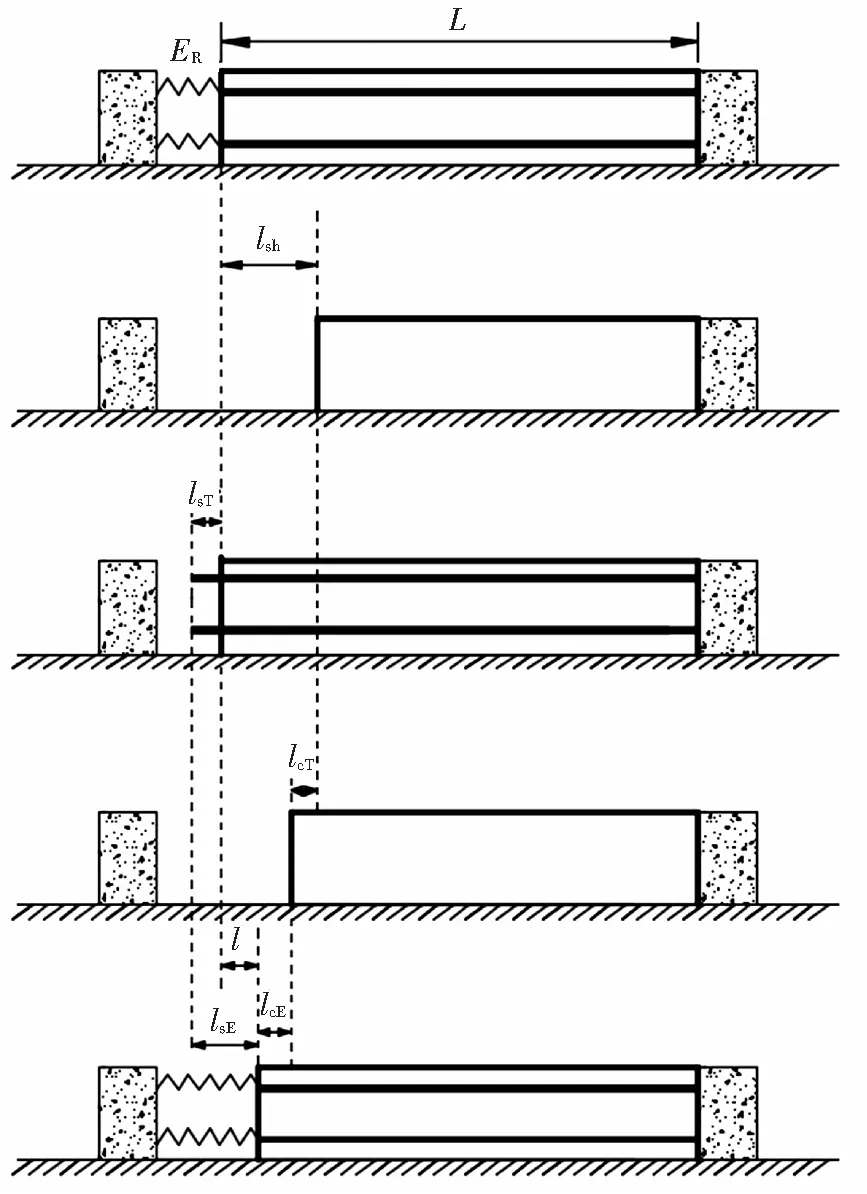
圖2 約束應力計算模型

2.2 徐變變形的修正

根據應力松弛系數法計算受徐變影響的約束應力，并將時間離散，分別計算等長時間段內的應力增量，然后疊加，可得某時刻的應力值:

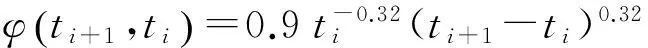
2.3 開裂風險分析

混凝土早齡期抗拉強度可以用水化度來推算[20]：

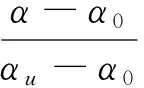
(22)

式中：ζ為經驗常數，取1.1；f28為混凝土28 d抗拉強度，取3.1 MPa；τ為經驗常數，取0.5.

一般將混凝土在某時刻的實際拉應力與抗拉強度的比值σ(t)/f(α)作為開裂風險，但混凝土的力學性能具有明顯的波動性，一般認為當開裂風險達到0.7時，混凝土開裂的可能性需要足夠的重視[21].

3 計算結果與分析

3.1 模型驗證

文獻[4]提供了水膠比為0.30，截面尺寸為60 mm×100 mm的混凝土軸向自由收縮構件28 d齡期內溫度、相對濕度和應力的試驗結果，以此作為對計算模型正確性的驗證.其混凝土配比見表3.

表3 混凝土配合比

圖3、4為相對濕度、溫度和應變的計算值與參考文獻試驗結果的對比.結果表明：相對濕度在3 d～14 d范圍內模型計算值較試驗值略大，主要因為模型計算過程未考慮試驗中出現的泌水現象引起的水分分布不均勻；澆筑完成至4 d的應變計算值比試驗值小，是因為模型僅考慮化學縮減和干縮這兩類主要的變形來源，未考慮沉降變形和塑性變形等因素；隨著相對濕度的降低，構件軸向應變逐漸增大，截面中心相對濕度在28 d達到50.45%，對應的應變值為1.04×10-3；由于水化放熱的影響，溫度在1 d～3 d齡期出現明顯升高，之后與環境溫度變化基本一致；采用本文的計算方法，可以較好地描述混凝土早齡期相對濕度、應變和溫度的變化規律.

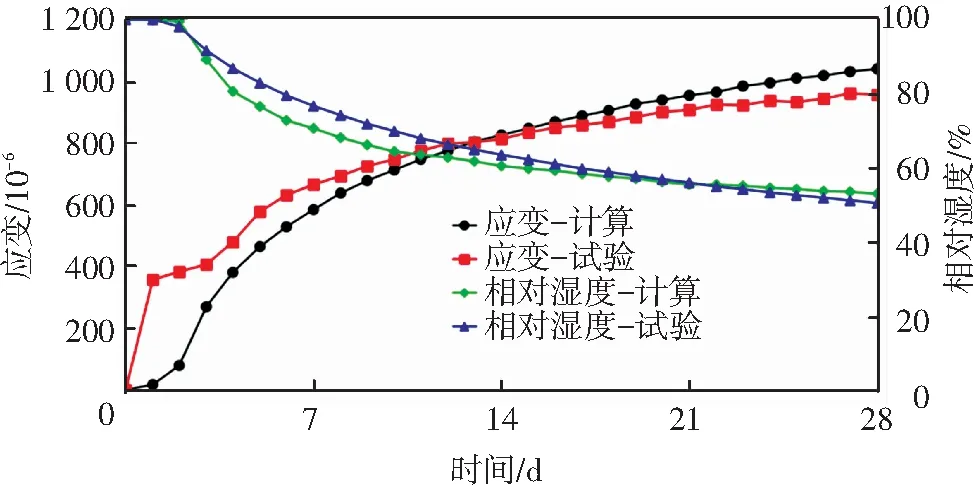
圖3 模型計算結果與文獻試驗結果的比較

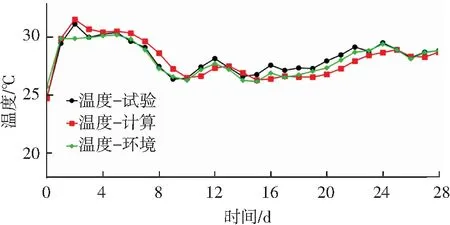
圖4 計算溫度與文獻試驗結果的比較

3.2 溫濕耦合分析

JGJ/T 281—2012《高強混凝土應用技術規程》中規定，高強混凝土可采取潮濕養護，并可采取蓄水、澆水、噴淋灑水或覆蓋保濕等方式，潮濕養護時間不宜少于10 d，因此，下文算例選擇對截面尺寸60 mm×100 mm的C80高強混凝土構件28 d齡期內的溫濕度耦合效應進行計算分析，澆水養護時間為10 d，然后置入溫度20 ℃，相對濕度20%的環境中.

濕度擴散系數會受到濕度和溫度的雙重影響.由圖5可知，相對濕度大于60%時，擴散系數較大，此時混凝土內部的液態水含量較高，對擴散性的影響顯著[10]，相對濕度小于60%時，擴散系數基本保持不變；相對濕度大于60%時，隨著溫度的升高，擴散系數也明顯增大，當相對濕度為100%時，60 ℃時的擴散系數為20 ℃時擴散系數的2.3倍.從圖6可以看出，混凝土溫度在7 d齡期內有明顯的升溫和降溫過程，最大升溫不超過3 ℃，考慮耦合作用的混凝土擴散系數在7 d齡期內出現明顯變大，但由于養護時間為10 d，因此對濕度擴散和混凝土變形的影響較小；7 d至28 d齡期，耦合效應對擴散系數影響極小.

圖5 擴散系數隨相對濕度的發展

圖6 擴散系數和溫度隨時間的發展

由圖7可知，相對濕度為100%時，水化熱影響系數β(H)為1，當相對濕度為80%時，β(H)為0.5，若相對濕度降為60%，則β(H)為0.059，因此，相對濕度對水化熱的影響明顯，這一點也可由圖8看出，濕度為100%的最大絕熱溫升為60%時的16.9倍，80%時的2倍，相關文獻研究指出，當相對濕度降低到約75%時，水化反應會大大減緩或者停滯[22].由圖8還可知，耦合效應對相對濕度的影響極小，由于混凝土溫度變化明顯的7 d齡期內是處于澆水養護條件下，對混凝土早齡期的濕度影響極小，可忽略不計.

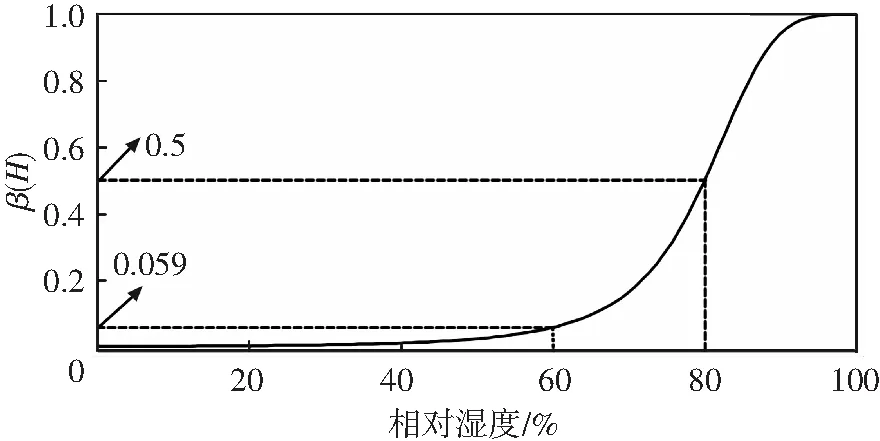
圖7 水化熱影響系數隨相對濕度的發展

Fig.7 Effect of hydration heat coefficient with the development of relative humidity

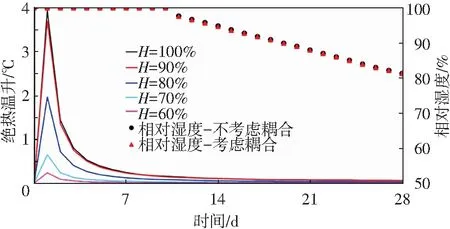
圖8 相對濕度和絕熱溫升隨時間的發展

3.3 應力及開裂風險分析

計算了環境溫度20 ℃，環境濕度20%的環境條件下，配筋率為1.5%，截面尺寸為60 mm×100 mm，約束度為1的C80高強混凝土的28 d齡期內應力變化規律和開裂風險，見圖9、10.

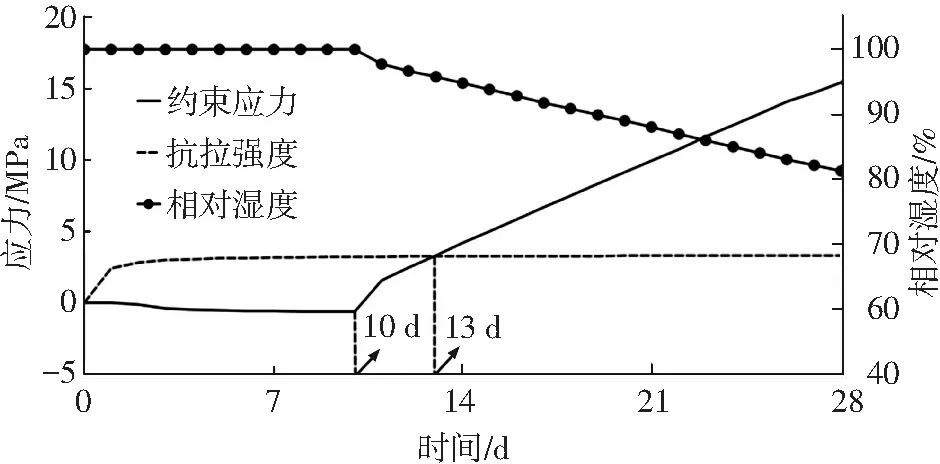
圖9 應力與相對濕度

圖10 開裂風險

由圖9可知，相對濕度在10 d齡期內基本為100%，養護結束后開始下降，28 d齡期降至81.3%；應力在10 d齡期內基本為0 MPa，10 d齡期后開始上升，在13 d齡期達到混凝土抗拉強度，28 d達到15.4 MPa.11 d齡期的開裂風險達到0.7，實際工程中有可能在28 d之前出現開裂，使應力得到釋放，所以應力不會達到15.4 MPa.由圖10可知，10 d齡期內的開裂風險基本為0，12 d齡期的開裂風險達到0.7，12 d至28 d齡期開裂風險呈線性增長.

4 結 論

1)建立的溫濕耦合變形計算模型能夠較好預測高強混凝土溫度、相對濕度和應變的變化.

2)相對濕度較高時，溫度對擴散系數的影響較明顯，對應的水化熱影響系數變化幅度大.

3)在澆水養護條件下，小體積混凝土的溫濕耦合作用不明顯；由于水化升溫較小，溫度對約束應力的影響可以忽略；養護結束以后相對濕度對約束應力的影響明顯，會使構件開裂風險變大.

[1] 朱伯芳.大體積混凝土溫度應力與溫度控制[M].北京:中國電力出版社,1999.

ZHU Bofang. Thermal stresses and temperature control of mass concrete[M]. Beijing: China Electric Power Press, 1999.

[2] BAZANT Z P, NAJJAR L J. Nonlinear water diffusion in nonsaturated concrete[J]. Materials and Structures, 1972, 5 (1): 3-20.

[3] 杜明月.基于微孔結構演化的早齡期混凝土熱-濕-力耦合模型研究[D].浙江:浙江大學,2015.

DU Mingyue. Thermo-hygro-mechanical model of early-age concrete based on micro-pore structure evolution[D]. Zhejiang: Zhejiang University, 2015.

[4] 侯東偉.混凝土自身與干燥收縮一體化及相關問題研究[D].北京:清華大學,2010.

HOU Dongwei. Integrative studies on autogenous and drying shrinkage of concrete and related issues[D]. Beijing: Tsinghua University, 2010.

[5]康明.施工期鋼筋混凝土構件的約束收縮變形性能研究[D].重慶:重慶大學,2010.

KANG Ming.A thesis submitted to chongqing university in partial fulfillment of the requirement for the degree of doctor of engineering[D]. Chongqing: Chongqing University, 2010.

[6] GAWIN D, PESAVENTO F, SCHREFLER B A. Hygro-thermo-chemo-mechanical modelling of concrete at early ages and beyond, Part I: hydration and hygro-thermal phenomena[J]. International Journal for Numerical Methods in Engineering, 2006, 67: 299-331.

[7] SCHINDLER A K, FOLLIARD K J. Heat of hydration models for cementitious materials[J]. ACI Materials Journal, 2005, 102(1): 24-33.

[8] PANE I, HANSENA W. Concrete hydration and mechanical properties under nonisothermal conditions[J]. ACI Materials Journal, 2002, 99(6): 534-422.

[9] ZHANG J, QI K, HUANG Y. Calculation of moisture distribution in early age concrete[J]. ASCE Journal of Engineering Mechanics, 2009, 135(8): 871-880.

[10]杜明月,田野,金南國,等.基于水泥水化的早齡期混凝土溫濕耦合[J].浙江大學學報(工學版),2015,49(8):1410-1416.

DU Mingyue, TIAN Ye, JIN Nanguo, et al. Coupling of hygro-thermal field in early-age concrete based on cement hydration[J]. Journal of Zhejiang University(Engineering Science), 2015,49(8): 1410-1416.

[11]OH B H, CHA S W. Nonlinear analysis of temperature and moisture distributions in early-age concrete structures based on degree of hydration[J]. ACI Materials Journal, 2003, 100(5):361-370.

[12]YUAN Y, Wan Z L. Prediction of cracking within early-age concrete due to thermal, drying shrinkage and creep behavior[J]. Cement & Concrete Research, 2002, 32(7): 1053-1059.

[13]張智博,張君.混凝土收縮與環境濕度的關系研究[J].建筑材料學報,2006,9(6):720-723.

ZHANG Zhibo, ZHANG Jun. Experimental study on relationship between shrinkage strain and environmental humidity of concrete [J]. Journal of Building Materials, 2006, 9(6): 720-723.

[14]BENTZ D P, GARBOCZI E J, QUENARD D A. Modeling drying shrinkage in reconstructed porous materials: application to porous Vycor glass[J]. Modeling And Simulation In Materials Science And Engineering, 1999, 6(3):211-236.

[15]ZHANG Jun, HOU Dongwei, HAN Yudong. Micromechanical modeling on autogenous and drying shrinkages of concrete[J]. Construction and Building Materials, 2012, 29(3): 230-240.

[16]JENSEN O M. Autogenous deformation and RH-change-self-desiccation and self-desiccation shrinkage[M]. Denmark: The Technical University of Denmark, 1993.

[17]BARY B, RANC Q, DURAND S. A coupled thermo-hydro-mechanical-damage model for concrete subjected to moderate temperatures[J]. International Journal of Heat and Mass Transfer, 2008, 51 (11/12):2847-2862.

[18]DU Mingyue, JIN Xianyu, YE Hailong, et al. A coupled hygro-thermal model of early-age concrete based on micro-pore structure evolution[J]. Construction and Building Materials, 2016, 111: 689-698.

[19]SCHUTTER G D. Applicability of degree of hydration concept and maturity method for thermo-visco-elastic behaviour of early age concrete[J]. Cement & Concrete Composites, 2004, 26:437-443.

[20]GUTSCH A W. Properties of early age concrete-Experiments and modelling [J]. Materials and Structures, 2002, 35(2):76-79.

[21]SPRINGENSCHMIDR. Prevention of thermal cracking in concrete at earlyages [M]. London: E& FN Spon, 1998: 60-62.

(編輯趙麗瑩)

Calculationofhygro-thermalcouplingstresscalculationandcrackingriskanalysisforhighperformanceconcrete

YOU Weijie, WANG Youzhi, ZHANG Xue, XU Gangnian, WANG Shimin

(School of Civil Engineering, Shandong University, Jinan 250000, China)

To reveal the rule of high strength concrete stress under the influence of hygro-thermal coupling and the cracking risk, the calculation method of hygro-thermal coupling and the calculation method of early age restraint shrinkage stress were established taking the concrete prism as an example. The simulation of temperature and humidity field was realized by programming. The results show that the model of hygro-thermal coupling can predict the development of temperature and humidity change in the early age of high performance concrete from 1day to 28 days. Under the condition of watering, the hygro-thermal coupling effect has little effect on the temperature field, humidity field and stress of high performance concrete, and the restraint stress and cracking risk are growing rapidly after stoping curing. The curing and atmosphere have remarkable influence on the early ages stress and cracking risk for high strength concrete.

shrinkage and creep; hygro-thermal coupling; restrained stress; finite difference method; cracking risk

10.11918/j.issn.0367-6234.201705174

TU528

A

0367-6234(2017)12-0170-06

2017-05-31

國家自然科學基金(11372165)

尤偉杰(1988—)，男，博士研究生；

王有志(1964—)，男，教授，博士生導師.

王有志，wyz96996@163.com