基于隊列理論的云資源分配收益最大化算法
鄭宇超 夏學文 艾冬梅
1(華東交通大學軟件學院 江西 南昌 330013) 2(北京科技大學數理學院 北京 100083)
基于隊列理論的云資源分配收益最大化算法
鄭宇超1夏學文1艾冬梅2
1(華東交通大學軟件學院 江西 南昌 330013)2(北京科技大學數理學院 北京 100083)
為了優化資源分配收益,提出基于時間服務因子TSF資源定價機制下的資源分配算法。首先,算法將資源分配問題形式化為隊列模型,并構建了收益最大化函數。然后,通過Lagrange乘子法求解最優化函數的解。利用時間服務因子,算法分別通過安全滿意度因子ASF和響應滿意度因子RSF定義了資源的定價方式,并同步考慮定價、請求到達率、資源服務率及可用資源量,得到了使收益最大化的資源分配方式。實驗結果表明,與傳統的啟發式資源分配算法比較,該算法得到的收益更高,且尤其在云資源數量較稀少的場景下,算法將更加具有優勢。
隊列理論 資源分配 云計算 收益最大化
0 引 言
云計算旨在通過虛擬化技術將IT資源整合成為大規模可擴展的資源池,并且以Internet作為載體提供軟件(SaaS)、平臺(PaaS)及基礎設施(IaaS)等形式的服務[1]。以服務提供者角度來講,云計算可以為終端用戶提供池化的資源,提供者的目標是租用各類服務并獲得收益。云服務的使用模式通常以預先支付或即付即用為主,用戶方只需要對請求服務或消費服務進行付費[2]。服務提供過程中,服務等級協議SLA供求雙方協作的重要問題。消費者主要通過服務質量QoS參數明確請求服務的等級。SLA通常根據可用性、響應時間等對資源分配的責任、擔保或性能等級進行具體描述。本文將以定價機制描述供求雙方需要服從的SLA。
對于服務提供者,在用戶服務實例間進行合理資源分配對最終獲得收益是至關重要的,即使對于相同的資源分配,收益也會隨著不同的分配策略產生極大變化。因此,本文將重點關注于如何基于SLA和可度量的服務屬性,管理資源分配并提供可區分的性能等級,以便最大化收益。
相關研究中,文獻[3]將云資源配置多目標優化定義為博弈問題,以服務質量和柔性指標多目標函數作為資源方和用戶方博弈雙方的收益函數,并通過GA算法對收益函數進行了求解。文獻[4]對任務類型偏好與資源服務能力差異進行了區分,在此基礎上提出了一種基于區分服務的演化博弈調度算法,可以極大提高用戶QoS。文獻[5]為了實現總利益最大化,通過建立服務提供商間的合作關系,提出了一種云資源分配的協作博弈模型。文獻[6]采用時間矩陣和費用矩陣作為云任務效益的衡量指標,提出一種基于效益博弈的資源動態可協調分配算法,通過構建效益博弈模型,以一種動態協調機制對博弈進行了求解。文獻[7]為解決資源競爭問題,提出通過建立用戶聯盟增加用戶效用,提高資源分配效率,但作者缺乏對模型的實驗驗證與分析。
不同于以上工作,本文的研究主要集中于:1)以隊列理論對云資源分配問題進行建模,模型綜合考慮了資源量、請求到達率、服務時間及資源定價等QoS參數。2)基于時間服務設計了兩種定價機制下的資源分配算法,目標是最大化資源提供收益。
1 系統模型
1.1 數學模型
假設云數據中心的服務器數量為N,服務提供者與m個用戶間以SLAs的形式簽訂服務協議,每個用戶(服務實例)可以通過服務器的資源分配獲得相應服務。考慮分配給每個服務實例i的ni個服務器可作為一個超級服務器,超級服務器的能力正比于其服務器數量。設系統中的服務實例請求服從泊松分布,其平均服務到達率為λ,服務器對其處理時間服從負指數分布,其平均服務率為1/μ,其中,μ表示單位時間內處理請求的數量。服務器對服務請求的執行由于運行環境的轉換需要付出代價,如:花費時間從外部存儲中讀取新到用戶的相關數據,因此,與單個服務實例相關的一組服務器可構建為基于FIFO的M/M/1隊列模型,定義服務強度ρ為請求到達率與單個服務器的服務率之比。系統模型的相關參數說明如表1所示。
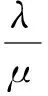
(1)

表1 符號說明
1.2 基于定價模型的時間服務因子TSF
1.2.1 服務性能指標
通常,云服務通過性能完成情況收取費用。為了評估性能,通常有兩種與響應時間相關的常用指標:平均響應時間MRT與時間服務因子TSF。其中,MRT是評估服務性能的常用指標,但無法反映響應時間出現大范圍波動的情況;而TSF可定義為確定時間間隔(時間槽)內的服務百分比,不僅可以反映響應時間,還可以精確描述響應時間的分布。本文將TSF定義為一個二元組
基于用戶需求與TSF,本文設計了兩種指標:安全滿意度因子ASF和響應滿意度因子RSF。同時,ASF與RSF均可以反映獲取性能與用戶服務需求之間的偏差。根據TSF定義用戶需求為二元組
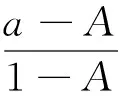
(2)
其中:a表示在響應時間要求為R時實際獲取的安全因子,即響應時間小于R時的服務率,fA表示實際獲取性能與用戶要求間的偏差。式(2)表明,若fA大于或等于0,獲取性能可滿足用戶要求,若獲取性能無法滿足用戶要求,則fA小于0。
同樣地,根據TSF定義用戶需求為
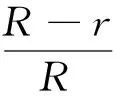
(3)
其中:r表示獲得的安全因子要求為A時的響應時間。式(3)表明,若fR大于或等于0,獲取性能可滿足用戶要求,若獲取性能無法滿足用戶要求,則fA小于0。
為了計算在一個時間槽內單個服務實例的第A個百分位響應時間,需要:
1) 記錄單個服務實例在一個時間槽內所有服務對應所有響應時間;
2) 對以上所有記錄進行升序排列;
3) 選擇有序序列中第A個記錄作為最終結果。
1.2.2 定價模型
本文基于ASF和RSF設計了兩種需求驅動的資源定價模型。將服務實例的服務提供時間劃分為固定步長的時間段,如
根據ASF和RSF定義以下兩種定價模型:
(4)
或
(5)
其中:服務提供價格B分別表示fA與fR的線性函數。兩種定價模型如圖1所示。

圖1 基于時間服務因子的定價模型
1.2.3 基準價格
根據M/M/1模型的隊列理論,服務滯留時間的累積分布時間為:
w(t)=1-e(λ-μ)t
(6)
假設需求為
A=1-e(λ-nμ)R
(7)
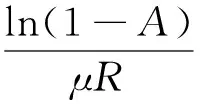
(8)
式(8)表明n臺服務器可確保用戶性能需求
(9)
由于服務請求到達率是動態變化的,可通過采樣統計獲取平均到達率。
2 資源分配最優化
2.1 基于ASF的資源分配最優化
假設服務實例i分配ni臺服務器,其性能需求為
ai=1-e(λi-niμi)Ri
(10)
將式(10)代入式(2),服務實例i的性能由指標ASF表示為:
(11)
根據定價模型式(4),服務實例i的服務提供獲得的平均收益為:
(12)
則單位時間內服務實例i獲得的總收益為:
(13)
因此,最優化問題可形式為:
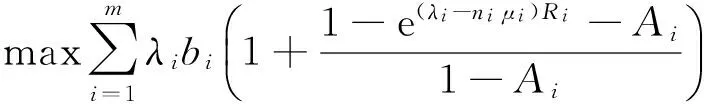
(14)
構造Lagrange函數:
(15)
其中:λ表示Lagrange乘子。
令dL/dni=0,i=0,1,2,…,m,則:
(16)
(17)
將式(17)代入式(14)中的約束條件中:
(18)
(19)
將式(19)代入式(17),則:

(20)
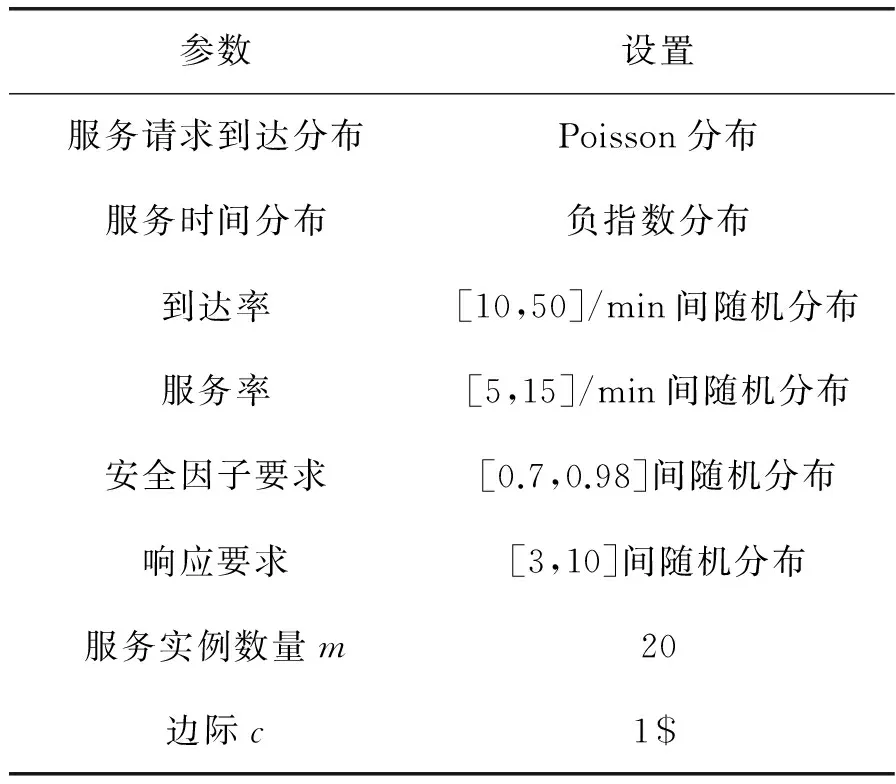
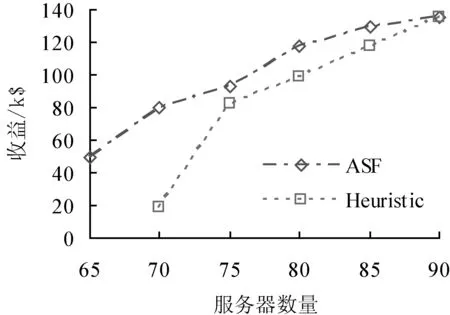
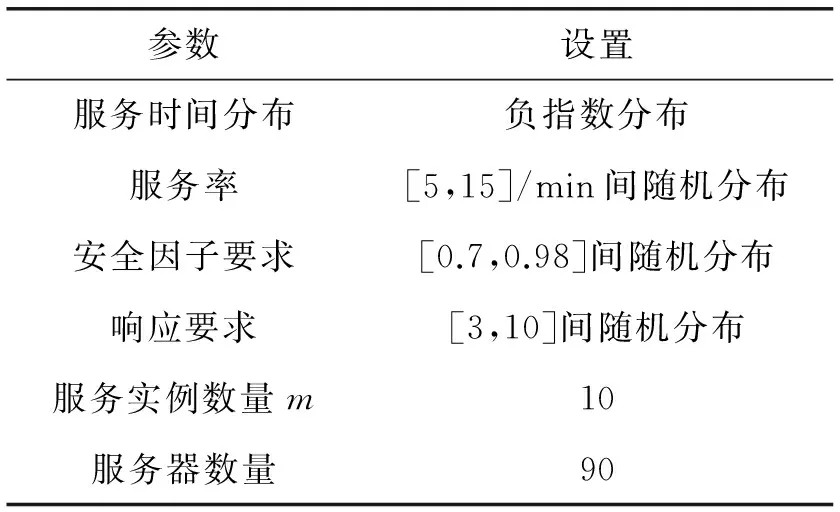
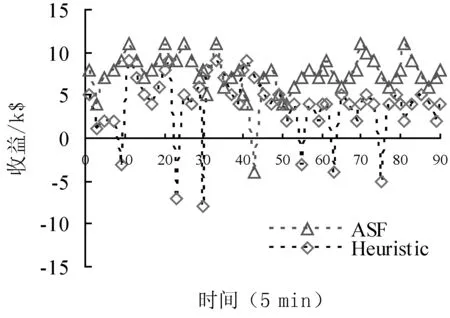
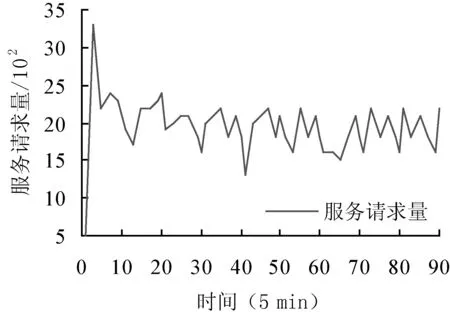
假設每個服務實例的請求到達率以式(6)建立模型,然而,只有當服務實例請求到達率小于服務處理速率時式(6)才是有效的。否則,基于FIFO隊列的響應時間將無法收斂,且響應時間會隨著時間增加。因此,只有當到達率小于服務處理速率時,式(20)才成立。
λi (21) ni>ρi (22) 圖1(a)表明若ai等于Ai,收益將不再增長。因此,一旦響應需求被滿足,對于服務實例i則無須繼續增加資源量。由式(8)可知: (23) 因此,式(22)與式(23)分別表示服務實例i對資源請求的下限與上限。 2.2 基于RSF的資源分配最優化 假設服務實例i分配ni臺服務器,其性能需求為 ai=1-e(λi-niμi)ri (24) 服務實例i的第Ai個響應時間為: (25) 將式(25)代入式(5),服務實例i的性能為: (26) 根據定價模型式(5),服務實例i的服務提供獲得的平均收益為: (27) 則單位時間內服務實例i獲得的總收益為: (28) 因此,最優化問題可形式為: (29) 構造Lagrange函數: (30) 其中:λ表示Lagrange乘子。 令dL/dni=0,i=0,1,2,…,m, (31) (32) 將式(32)代入式(29)中的約束條件: (33) (34) 將式(34)代入式(32),則: (35) 基于同樣的原因,式(32)與式(35)分別表示服務實例i對資源請求的下限與上限。 本節通過仿真實驗對算法性能進行分析,實驗工具為CloudSim[9]。實驗中分別以合成數據集與追蹤數據集作為兩種服務請求類型進行實驗測試。選擇文獻[10]中的Heuristic算法作為比較,服務收益作為算法性能比較的主要指標。ASF與RSF算法分別表示基于ASF與RSF的最優分配算法。相關參數與取值如表2所示。 表2 合成數據集測試參數 3.1 合成數據集測試分析 圖2和圖3表示三種算法在不同的定價機制下服務器資源量與收益間的關系。實驗中時間間隔設置為1小時。可以看出,ASF與RSF算法均優于Heuristic算法。當服務器數量為70和80時,Heuristic算法得到的收益分別比ASF算法低75.5%和16.2%,服務器數據為70時,RSF算法收益比Heuristic算法高53.4%。同時,隨著服務器數量的增加,Heuristic算法的曲線走勢基本與ASF與RSF算法是接近的。當服務器數量到達90后,三種算法的收益接近相等,這主要是由于當云數據中心有充足的服務器資源提供給服務實例時,大多數服務實例將分配以上限值定義的相同資源量。明顯地,當資源量相對不充足時,ASF與RSF算法具有更加明顯的優勢。因此,當資源量較少或服務實例量較大時,ASF與RSF算法可以優化資源分配得到更大的收益。 圖2 ASF定價下的收益 圖3 RSF定價下的收益 3.2 追蹤數據集測試分析 追蹤數據集選取文獻[11]中互聯網HTTP請求WWW服務器的相關數據集,如表3所示。本文將追蹤時間劃分為時間槽,步長為5 min。執行過程中,將每個時間槽中的到達請求進行統計,并根據先前記錄預測下一時間槽的平均到達率,預測機制可形式化為: λpost=λ+(λ-λpre) (36) 其中:λpost表示下一時間槽的到達率,λpre和λ分別表示前一個時間槽的測量到達率和當前時間槽的測量到達率。 表3 追蹤元數據 對于每個服務實例,服務器被劃分為10組,每組作為一個FIFO等待隊列。每個時間槽結束時,系統根據下一時間槽預測的到達率,重新在服務實例間進行資源分配。具體參數如表4所示。 表4 追蹤數據集測試參數 圖4和圖5表明實驗中部署90個服務器時每5 min收益變化的情況。總體看來,ASF與RSF算法均是優于Heuristic算法的。ASF與Heuristic算法每5 min的平均收益約為8.2 k$和1.6 k$,ASF算法約是Heuristic算法的4倍。RSF與Heuristic算法每5 min的平均收益約為8.7 k$和6.6 k$,前者約比后者高32%。同時可以看出,當資源量較少或服務實例量較大時,ASF與RSF算法可以優化資源分配得到更大的收益。在第47個時間槽時ASF與RSF算法的收益急劇減少,甚至低于Heuristic算法,這主要是由于服務到達率極端波動變化導致的。正如圖6中,在第42至45個時間槽時到達率正在降低,而在46個時間槽又急劇增加。因此,通過式(36)預測到達率并非一定準確,可能會導致資源分配的不合理。同時,由于ASF和RSF算法的準確性及Heuristic算法可能出現的不合理性,ASF和RSF算法將更加依賴于對到達率準確的預測。 圖4 ASF算法的收益進化過程 圖5 RSF算法的收益進化過程 圖6 服務請求到達 為了促進終端用戶與服務提供者之間的協作關系,基于SLA形式的時間服務因子TSF,提出了基于定價機制的收益最大化算法。算法以隊列理論建立了服務到達與服務提供模型,并通過Lagrange乘子法構建了最優化目標函數,并對函數進行了求解。實驗結果表明,所提算法性能優于傳統啟發式分配算法,尤其在資源短缺的云計算環境下,算法具有更加明顯的優勢。 [1] Cusumano M. Cloud computing and SaaS as new computing platform[J].Communication of the ACM, 2011,53(4):27-29. [2] Guo L, Zhao S, Shen S,et al. Task scheduling optimization in cloud computing based on heuristic algorithm[J].Journal of Networks, 2012,7(3):547-553. [3] 蘇凱凱,徐文勝,李建勇. 云制造環境下基于非合作博弈的資源優化配置方法[J].計算機集成制造系統,2015,21(8):2228-2239. [4] 李陶深,張希翔. 云計算下區分服務的演化博弈調度算法[J]. 北京郵電大學學報,2013,36(1):41-45. [5] 朱匆,劉元君,彭自然,等. 移動云計算中基于協作式博弈模型的資源分配方案[J].計算機應用研究,2014,31(3):912-916. [6] 李衛平,武海燕,楊杰. 基于效益博弈的云計算資源動態可協調分配策略研究[J].計算機工程與科學,2016,38(1):57-61. [7] Ergu D, Kou G, Peng Y,et al. The analytic hierarchy process: task scheduling and resource allocation in cloud computing environment[J]. The Journal of Supercomputing, 2013,64(3):835-848. [8] Xu Zhongsheng, Shen Subin. A multi-objective optimization scheduling method in cloud computing[J]. Microcomputer Its Application, 2015,34(13):17-20. [9] Rodrigo C, Rajiv R, Anton B, et al. CloudSim: a toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms[J]. Software: practice and experience, 2011,41(1):23-50. [10] Mazzucco M. Revenue maximization problems in commecial data centers[D].PhD Thesis,University of Newcastle, Newcastle,UK,2014. [11] Internet Traffic Archive[OL]. 2011-8-23. Http://ita.ee.lbl.gov/html/traces.html. PROFITMAXIMIZATIONALGORITHMFORCLOUDRESOURCEALLOCATIONBASEDONQUEUETHEORY Zheng Yuchao1Xia Xuewen1Ai Dongmei2 1(SchoolofSoftware,EastChinaJiaotongUniversity,Nanchang330013,Jiangxi,China)2(SchoolofMathematicsandPhysics,UniversityofScienceandTechnologyBeijing,Beijing100083,China) For optimizing the profit of resource allocation, a resource allocation algorithm in resource pricing mechanism based on time service factor is proposed. First, the resource allocation problem was formalized as the queue model, and the profit maximization function was constructed. Then, the profit maximization function was solved by Lagrange multiplier method. Using the time service factor, our algorithm defined the pricing mode respectively by the assurance satisfaction factor and responded satisfaction factor. In addition, resource allocation was maximized by considering pricing, request arrival rates, resource service rates, and available resources. Experimental results show that compared with the traditional heuristic allocation algorithm, our algorithm yields higher returns, especially in the context of the scarcity of cloud resources. The proposed algorithm will have more advantages. Queue theory Resource allocation Cloud computing Profit maximization 2017-01-09。江西省教育廳科研項目(GJJ150539)。鄭宇超,講師,主研領域:云計算及應用。夏學文,副教授。艾冬梅,高工。 TP393 A 10.3969/j.issn.1000-386x.2017.11.047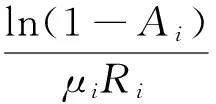
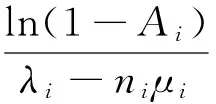
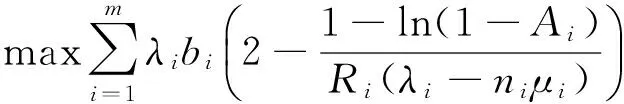
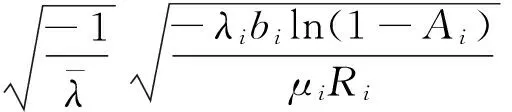
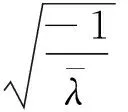
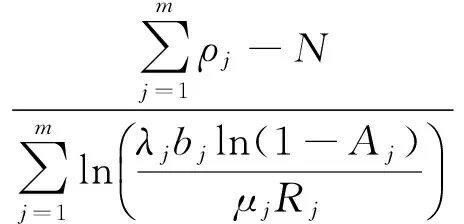
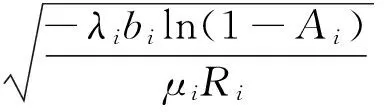
3 實驗分析
4 結 語

