圓環(huán)結(jié)構(gòu)磁光光子晶體中的拓撲相變?

沈清瑋 徐林 蔣建華2)

1)(蘇州大學(xué)物理與光電.能源學(xué)部,蘇州 215006)2)(蘇州大學(xué),2011蘇州納米科技協(xié)同創(chuàng)新中心,蘇州 215006)

圓環(huán)結(jié)構(gòu)磁光光子晶體中的拓撲相變?

沈清瑋1)徐林1)蔣建華1)2)?

1)(蘇州大學(xué)物理與光電.能源學(xué)部,蘇州 215006)2)(蘇州大學(xué),2011蘇州納米科技協(xié)同創(chuàng)新中心,蘇州 215006)

(2017年8月30日收到;2017年11月8日收到修改稿)

二維圓環(huán)結(jié)構(gòu)的三角晶格磁光光子晶體中可以呈現(xiàn)多重拓撲相.在不同的幾何參數(shù)和磁場下,這些拓撲相包括正常光子帶隙相、量子自旋霍爾相和反常量子霍爾相.與文獻[1]類似,該結(jié)果展現(xiàn)了二維光子晶體豐富的拓撲相變現(xiàn)象.

光子晶體,拓撲相變,拓撲邊界態(tài)

1 引 言

1879年,美國物理學(xué)家Hall發(fā)現(xiàn)電流通過有垂直磁場的導(dǎo)體時會產(chǎn)生側(cè)向電壓,這一現(xiàn)象被稱為霍爾效應(yīng)[2].大約在100年后,也就是1980年,德國物理學(xué)家von Klitzing實驗觀測到在強磁場下,二維電子氣的霍爾電導(dǎo)呈現(xiàn)出階梯化的變化,被稱為整數(shù)量子霍爾效應(yīng)[3].1982年,Thouless等[4]指出這種整數(shù)化的霍爾效應(yīng)是由于能帶的非平庸拓撲性質(zhì)導(dǎo)致的.根據(jù)他們的理論,量子霍爾效應(yīng)中的整數(shù)對應(yīng)一種被稱為第一類陳數(shù)的拓撲量子數(shù).1988年,Haldane提出了在周期交錯的磁場下獲得量子化電導(dǎo)的方法.由于該方法總的磁通量為零,因而被稱為反常量子霍爾效應(yīng)(quantum anomalous Hall e ff ect,QAH e ff ect)[5].反常量子霍爾效應(yīng)通常用來指沒有朗道能級圖像的量子霍爾效應(yīng)系統(tǒng),特別是有磁性系統(tǒng)的量子霍爾效應(yīng)[6].雖然這個辦法不需要外加磁場,但是局域范圍內(nèi)體系的時間反演對稱性是被破壞的(time-reversal broken,TRB).2005年和2006年,Kane和Mele[7],以及Zhang等[8]分別提出了受時間反演對稱性保護的二維量子自旋霍爾效應(yīng)(quantum spin Hall e ff ect,QSHE)和三維拓撲絕緣體.量子自旋霍爾效應(yīng)和三維拓撲絕緣體由一種新的拓撲量子數(shù)描述,稱為Z2拓撲數(shù)(有時可以表示為“自旋陳數(shù)”,實際上是第二類陳數(shù)).隨后,在2011年拓撲晶體絕緣體[9]和Floquet拓撲絕緣體[10]相繼被提出.

從量子霍爾效應(yīng)和反常量子霍爾效應(yīng)到量子自旋霍爾效應(yīng),體系的時間反演對稱性質(zhì)從無到有.在量子霍爾效應(yīng)中,由于時間反演不對稱,只有單向傳輸?shù)氖中赃吔鐟B(tài)(chiral edge state).而在量子自旋霍爾效應(yīng)中,由于電子是費米子,時間反演對稱性保證了Kramers二重簡并(自旋簡并),從而導(dǎo)致了自旋反向的雙向?qū)菪吔鐟B(tài)(helical edge states):自旋上的電子朝一個方向運動,自旋下的電子朝相反的方向運動.如果在自旋量子霍爾效應(yīng)中引入微小的時間反演不對稱,原有的Kramers二重簡并將會出現(xiàn)分裂,但只要體系的帶隙不閉合,雙向?qū)ǖ倪吔鐟B(tài)仍然存在.這樣的體系可稱之為時間反演破壞的量子自旋霍爾效應(yīng)(TRB QSHE).如果進一步加大時間反演不對稱性,體系將會發(fā)生拓撲相變,帶隙會先閉合再打開,進入一個新的拓撲相,反常量子霍爾效應(yīng)相(QAH).QAH相存在單向?qū)ǖ倪吔鐟B(tài),所以拓撲相變的一個重要結(jié)果就是邊界態(tài)性質(zhì)的改變.通過改變時間反演對稱性破壞的程度,體系可以經(jīng)過QSHE到TRB QSHE,再到QAH的轉(zhuǎn)變過程.

在光子晶體學(xué)領(lǐng)域中,光子能帶的拓撲現(xiàn)象最早由Haldane和Raghu在2008年提出[11,12].他們在磁光光子晶體系統(tǒng)給出了實現(xiàn)光學(xué)的量子霍爾效應(yīng)的方案.隨后更多的光學(xué)的量子霍爾效應(yīng)和單向邊界態(tài)被人們廣泛地研究并在實驗上實現(xiàn)[13?15].由于光子屬于玻色子,沒有Kramers二重簡并,無法直接將量子自旋霍爾效應(yīng)和拓撲絕緣體的概念推廣到光子晶體.雖然如此,但是人們還是通過其他對稱性質(zhì)加上玻色系統(tǒng)的時間反演對稱構(gòu)造了類似電子系統(tǒng)的贗時間反演對稱和對應(yīng)的贗自旋1/2態(tài).這樣的贗自旋1/2態(tài)有利用光子偏振特性的TE+TM/TE-TM混合模式[16,17]和TE/TM模式[18]實現(xiàn)的二重簡并,也有利用空間對稱性質(zhì)的順時針/逆時針能流態(tài)[19]構(gòu)成的.因為時間反演對稱操作在電子自旋1/2態(tài)的作用數(shù)學(xué)上等價于贗時間反演對稱操作在贗自旋1/2態(tài)的作用,所以可以將電子的自旋量子霍爾效應(yīng)的拓撲上的結(jié)論映射到光子晶體體系中來.與此同時,通過連續(xù)破壞時間反演對稱性,也可以研究在光子體系中的拓撲相變的問題.

最近,Chen等[1]報道了在二維蜂窩狀晶格磁光光子晶體中,通過調(diào)控原胞的幾何結(jié)構(gòu)和外加磁場破壞時間反演對稱性質(zhì),可以實現(xiàn)光學(xué)中的自旋量子霍爾效應(yīng)相到時間反演破壞的自旋量子霍爾效應(yīng)相,再到反常量子霍爾效應(yīng)的相變過程.本文研究了在二維圓環(huán)結(jié)構(gòu)的磁光光子晶體中的拓撲相變問題.根據(jù)之前的工作[20]可知,無外磁場時,在三角晶格C6點群和真實的TR對稱構(gòu)造的贗TR對稱的保護下,通過調(diào)節(jié)圓環(huán)內(nèi)外徑大小,可以實現(xiàn)二維光子晶體的自旋量子霍爾態(tài)或者普通的絕緣態(tài).基于此,當逐漸增加外磁場時,由于磁光介質(zhì)的法拉第效應(yīng),破壞了體系的時間反演對稱,二維光子晶體將經(jīng)歷自旋量子霍爾效應(yīng)到時間反演破壞的自旋量子霍爾效應(yīng),再到反常量子霍爾效應(yīng)的相變過程.數(shù)值計算的能帶和拓撲邊界態(tài)證實了相變過程.本文的工作豐富了調(diào)控二維光子晶體的拓撲相變的方法.

2 光子晶體的結(jié)構(gòu)和相變

考慮的二維光子晶體是圓環(huán)磁光材料擺成的三角晶格體系.如圖1(a)所示,晶格常數(shù)為a,磁光材料的圓環(huán)內(nèi)外半徑分別為R1和R2.磁光材料為釔鐵石榴石(YIG),它的介電常數(shù)是它的磁導(dǎo)率張量為.這個張量取決于外磁場和光子頻率.它的取值由Drude模型決定[21],其中飽和磁化率4πMs=1884.通常在1600 Gauss的磁場和4.28 MHz下,YIG磁導(dǎo)率的張量元分別取κ=12.4u0和u=14u0.

圖1 二維光子晶體原胞結(jié)構(gòu)示意圖和能帶相變圖 (a)三角晶格晶格常數(shù)為a,背景是空氣,介電常數(shù)和真空磁導(dǎo)率分別為ε0和μ0,圓環(huán)結(jié)構(gòu)的內(nèi)外半徑R1和R2是可調(diào)控的;(b)在R1=0.334a和R2=0.429a(a=0.013 m)的原胞結(jié)構(gòu)時,無外加磁場下,光子晶體是QSHE的相,隨著外加磁場H的增大,體系發(fā)生了拓撲轉(zhuǎn)變Fig.1.The structure of unit cell and phase transition of two dimensional photonic crystal:(a)Lattice constant is a,dielectric constant and permeability of vacuum is ε0and u0respectively,the radius of ring structure R1and R2are tunable;(b)When R1=0.334a and R2=0.429a(a=0.013 m)without external magnetic field,photonic crystal is in QSHE When external magnetic field is increasing,the topology of this system is changing.

圖2 不同二維光子晶體能帶 (a)在無外磁場、R1=0.005a和R2=0.388a的原胞結(jié)構(gòu)A時,光子晶體在頻率為0.46附近是普通的絕緣相;(b)在外磁場H=600,R1=0.357a和R2=0.450a的原胞結(jié)構(gòu)B時,光子晶體在頻率為0.46附近是時間反演破壞的自旋量子霍爾效應(yīng)相;(c)在外磁場H=2200,R1=0.284a和R2=0.425a的原胞結(jié)構(gòu)C時,光子晶體在頻率為0.46附近是QAH相Fig.2.Di ff erent band structures in two dimensional photonic crystal:(a)When R1=0.005a and R2=0.388a without external magnetic field,photonic crystal is conventional insulator phase near the frequency of 0.46;(b)when R1=0.357a and R2=0.450a with external magnetic field H=600,photonic crystal is TRB a quantum spin Hall phase near the frequency of 0.46;(c)when R1=0.284a and R2=0.425a with external magnetic field H=2200,photonic crystal is QAH near the frequency of 0.46.

現(xiàn)在考慮橫向磁場(TM)模式的光子晶體本征態(tài)問題.由于三角晶格具有C6對稱性,所以光子晶體的能帶在Γ點處存在兩個二維不可約表示,分別為E1和E2[22].根據(jù)宇稱的不同,E1的兩個本征基態(tài)函數(shù)記為px和py,簡并頻率對應(yīng)ω1;而E2的兩個本征基態(tài)函數(shù)為記為dxy和dx2?y2,簡并頻率對應(yīng)ω2.兩個p態(tài)和d態(tài)可以分別構(gòu)成兩個贗自旋1/2態(tài),即和對于普通的絕緣相而言,d態(tài)的頻率高于p態(tài).但是通過調(diào)節(jié)內(nèi)外半徑大小和材料的電介質(zhì)參數(shù),可以實現(xiàn)p態(tài)和d態(tài)的偶然簡并,甚至能帶的反轉(zhuǎn)[20],這樣就實現(xiàn)了光子的自旋量子霍爾相.如果普通的絕緣相和自旋量子霍爾相具有共同的帶隙,那么在它們的邊界上可以找到受體態(tài)拓撲性質(zhì)保護的拓撲邊界態(tài).

加入外加磁場后,原來簡并的贗自旋態(tài)的能級會劈裂.如圖1(b)所示,在H=0時,光子晶體是自旋量子霍爾效應(yīng)相,p態(tài)的頻率高于d態(tài).隨著外加磁場的增加,體系變成時間反演破壞的自旋量子霍爾效應(yīng)相.在H到達1700 Gauss時,體系變成了反常量子霍爾效應(yīng)相.本文的能帶結(jié)構(gòu)和邊界態(tài)是由商業(yè)軟件COMSOL MULTPHYSICS計算的.考慮到所關(guān)心的能帶頻率處于10 GHz到14 GHz之間,對于有效的Drude參數(shù),采取該頻率段的平均值.晶格常數(shù)選取a=0.013 m來討論能帶結(jié)構(gòu)的拓撲相變.

圖2展現(xiàn)了3種不同拓撲相的能帶圖.其中A和B分別為普通的絕緣相和時間反演破壞的自旋量子霍爾效應(yīng)相,它們在0.46附近有共同的帶隙.體系C是QAH相.

3 拓撲邊界態(tài)

圖2所示的三種不同拓撲相A,B和C有共同的帶隙.由于A和B的能帶具有不同的陳數(shù),根據(jù)拓撲能帶理論中體態(tài)邊界態(tài)的對應(yīng)關(guān)系,如果A和C放在一起,將會在它們的邊界上出現(xiàn)受拓撲性質(zhì)保護的單向傳輸?shù)氖中赃吔鐟B(tài).我們用32個原胞構(gòu)成長條狀的超原胞,如圖3(a),并計算得到該超原胞的投影能帶圖.在投影能帶圖中可以看出0.46頻率點附近有表面態(tài)的色散關(guān)系.圖3(b)和圖3(c)分別展示了在s1和s2交面處ky=?0.2π/a表面態(tài)的Ez的場分布.可以看出兩者是同一種模式,只是在不同的交面而已,它們是單向傳輸?shù)?因而單向傳輸?shù)倪吔鐟B(tài)的存在說明了A和B的能帶陳數(shù)的不同.

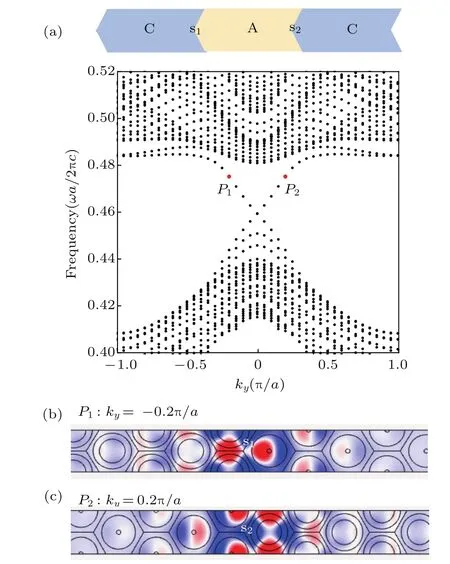
圖3 投影能帶和陳數(shù)不同所導(dǎo)致的拓撲邊界態(tài) (a)計算由圖2中A和C兩種光子晶體各16個原胞構(gòu)成的長條狀的超原胞的投影能帶,s1和s2為左右兩個界面;(b)在能帶P1點處,ky= ?0.2π/a時,s1界面處拓撲邊界態(tài)Ez的場分布;(c)在能帶P2點處,ky=0.2π/a時,s2界面處拓撲邊界態(tài)Ez的場分布Fig.3.Projected band structure and topological edge states induced by the di ff erence of Chern number:(a)Super cell consists of 16 unit cell A and 16 unit cell C of Fig.2.Projected band structure is calculated with two di ff erent interfaces s1and s2;(b)Ez field of topological edge state at interface s1of P1with ky= ?0.2π/a;(c)Ez field of topological edge state at interface s2of P2with ky=0.2π/a.

類似地,由于A和B分別為普通的絕緣相和時間反演破壞的自旋量子霍爾效應(yīng)相,因而它們的能帶具有不同的Z2拓撲數(shù).如果A和B放在一起,將會在它們的邊界上出現(xiàn)受拓撲性質(zhì)保護的一對螺旋邊界態(tài).我們用32個原胞構(gòu)成長條狀的超原胞,如圖4(a),并計算得到該超原胞的投影能帶圖.在投影能帶圖中可以看出0.46頻率點附近有表面態(tài)的色散關(guān)系.圖4(b)和圖4(c)分別展示了在s1交面處ky=?0.2π/a表面態(tài)的Ez的場分布,構(gòu)成該體系的一對螺旋邊界態(tài).通常該對螺旋邊界態(tài)的能量是一樣的,但是本文的體系中由于s1交面和s2交面并非完全等價,且在邊界上的贗TR對稱性被破壞,因而造成兩個邊界態(tài)的能量的不同.

圖4 投影能帶和Z2拓撲數(shù)不同所導(dǎo)致的拓撲邊界態(tài)(a)計算由圖2中A和B兩種光子晶體各16個原胞構(gòu)成的長條狀的超原胞的投影能帶,s1和s2為左右兩個界面;(b)在能帶P1點處,ky= ?0.2π/a時,s1界面處拓撲邊界態(tài)Ez的場分布;(c)在能帶P2點處,ky=0.2π/a時,s1界面處拓撲邊界態(tài)Ez的場分布Fig.4.Projected band structure and topological edge states induced by the di ff erence of Z2topological number:(a)Super cell consists of 16 unit cell A and 16 unit cell B of Fig.2.Projected band structure is calculated with two di ff erent interfaces s1and s2;(b)Ez field of topological edge state at interface s1of P1with ky= ?0.2π/a;(c)Ez field of topological edge state at interface s1of P2with ky=0.2π/a.

4 結(jié) 論

利用磁光材料在三角晶格光子晶體中實現(xiàn)了多重拓撲相變.通過改變原胞的結(jié)構(gòu)和外磁場的大小,三角晶格光子晶體可以具有正常光子帶隙、量子自旋霍爾相和反常量子霍爾相,并且得到了手性邊界態(tài)和螺旋邊界態(tài).本文空心圓環(huán)的結(jié)構(gòu)比文獻[1]的結(jié)構(gòu)更為簡單,因此為實現(xiàn)光子晶體的拓撲相變提供了更多的方法.

[1]Chen Z G,Mei J,Sun X C,Zhang X,Zhao J,Wu Y 2017Phys.Rev.A95 043827

[2]Hall E H 1879Am.J.Math.2 287

[3]Klitzing K,Dorda G,Pepper M 1980Phys.Rev.Lett.45 494

[4]Thouless D,Kohmoto M,Nightingale M,den Nijs M 1982Phys.Rev.Lett.49 405

[5]Haldane F D M 1988Phys.Rev.Lett.61 2015

[6]Xiao D,Chang M C,Niu Q 2010Rev.Mod.Phys.82 1959

[7]Kane C L,Mele E J 2005Phys.Rev.Lett.95 226801

[8]Bernevig B A,Hughes T L,Zhang S C 2006Science314 1757

[9]Fu L 2011Phys.Rev.Lett.106 106802

[10]Lindner N H,Refael G,Galitski V 2011Nat.Phys.7 490

[11]Haldane F,Raghu S 2008Phys.Rev.Lett.100 013904

[12]Raghu S,Haldane F 2008Phys.Rev.A.78 033834

[13]Lu L,Joannopoulos J D,Solja?i? M 2014Nat.Photon.8 821

[14]Wang Z,Chong Y,Joannopoulos J,Solja?i? M 2009Nature461 772

[15]Wang Z,Chong Y,Joannopoulos J D,Solja?i? M 2008Phys.Rev.Lett.100 013905

[16]Chen W J,Jiang S J,Chen X D,Zhu B,Zhou L,Dong J W,Chan C 2014Nat.Commun.5 5782

[17]Khanikaev A B,Mousavi S H,Tse W K,Kargarian M,MacDonald A H,Shvets G 2013Nat.Mater.12 233

[18]Ma T,Khanikaev A B,Mousavi S H,Shvets G 2015Phys.Rev.Lett.114 127401

[19]Wu L H,Hu X 2015Phys.Rev.Lett.114 223901

[20]Xu L,Wang H X,Xu Y D,Chen H Y,Jiang J H 2016Opt.Express24 18059

[21]Pozar D M 2009Microwave Engineering(Hoboken:John Wileyamp;Sons)

[22]Sakoda K 2004Optical Properties of Photonic Crystals(Berlin:Springer Scienceamp;Business Media)

PACS:41.20.Jb,03.65.Vf,42.25.GyDOI:10.7498/aps.66.224102

*Project supported by the National Natural Science Foundation of China(Grant Nos.11675116)and the Faculty Startup Funding of Soochow University.

?Corresponding author.E-mail:jhjiang@hotmail.com

Topological phase transitions in core-shell gyromagnetic photonic crystal?

Shen Qing-Wei1)Xu Lin1)Jiang Jian-Hua1)2)?

1)(Department of Physics,Optoelectronics and Energy,Soochow University,Suzhou 215006,China)2)(Collaborative Innovation Center of Suzhou Nano Science and Technology,Soochow University,Suzhou 215006,China)

30 August 2017;revised manuscript

8 November 2017)

We found that core-shell gyromagnetic photonic crystal of two-dimensional triangular lattice exhibit topological phases.In a certain parameters and magnetic field,those phases could be a conventional insulator phase,a quantum spin Hall phase,and a quantum anomalous Hall phase.Di ff erent from the structure of Ref[1],phase transitions in our core-shell structure does not involve changes of space symmetry,which depend on parameters of our structure and the broken of time reverse symmetry.Our result shows the variety of topological phase transitions in photonic crystals.

photonic crystal,topological phase transition,topological edge state

10.7498/aps.66.224102

?國家自然科學(xué)基金(批準號:11675116)和蘇州大學(xué)科研啟動基金資助的課題.

?通信作者.E-mail:jhjiang@hotmail.com